Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wicks, Michael C.
Thomas, Flint O.
Corke, Thomas C.
Nelson, Chris
Patel, Mehul P.
and
Cain, Alan B.
2015.
Plasma Flow Control on a Landing Gear Model.
Liu, Hanru
and
Azarpeyvand, Mahdi
2016.
Passive Control of Tandem Cylinders Flow and Noise Using Porous Coating.
Liu, Hanru
and
Wei, Jinjia
2016.
On the role of surface permeability for the control of flow around a circular cylinder.
Journal of Vibroengineering,
Vol. 18,
Issue. 8,
p.
5406.
Brauner, Timothy
Laizet, Sylvain
Benard, Nicolas
and
Moreau, Eric
2016.
Modelling of Dielectric Barrier Discharge Plasma Actuators for Direct Numerical Simulations.
Asaumi, Norio
Matsuno, Shinsuke
Matsuno, Takashi
Sugahara, Masataka
and
Kawazoe, Hiromitsu
2017.
Multi-Electrode Plasma Actuator to Improve Performance of Flow Separation Control.
International Journal of Gas Turbine, Propulsion and Power Systems,
Vol. 9,
Issue. 1,
p.
1.
Liu, Hanru
Wang, Yangang
Wei, Jinjia
and
Qu, Zhiguo
2018.
The importance of controlling the upstream body wake in tandem cylinders system for noise reduction.
Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering,
Vol. 232,
Issue. 3,
p.
517.
Li, Ling
Liu, Peiqing
Xing, Yu
and
Guo, Hao
2019.
Experimental investigation on the noise reduction method of helical cables for a circular cylinder and tandem cylinders.
Applied Acoustics,
Vol. 152,
Issue. ,
p.
79.
He, Chuangxin
Liu, Yingzheng
and
Gan, Lian
2020.
Instantaneous pressure determination from unsteady velocity fields using adjoint-based sequential data assimilation.
Physics of Fluids,
Vol. 32,
Issue. 3,
Zhou, Di
Wang, Kan
and
Wang, Meng
2020.
Large-Eddy Simulation of an Axisymmetric Boundary Layer on a Body of Revolution.
Wang, Junye
Wang, Kan
and
Wang, Meng
2021.
Computational prediction and analysis of rotor noise generation in a turbulent wake.
Journal of Fluid Mechanics,
Vol. 908,
Issue. ,
Wong, Chi Wai
Shao, Xiao
Wang, Longjun
and
Zhou, Yu
2021.
A high-performing sawtooth plasma actuator with multi-electrodes.
Aerospace Science and Technology,
Vol. 119,
Issue. ,
p.
107221.
Zhou, Di
Wang, Kan
and
Wang, Meng
2021.
Computation of Rotor Noise Generation in a Thick Axisymmetric Turbulent Boundary Layer.
Niu, Xiao-Fei
Li, Yong
and
Wang, Xun-Nian
2021.
Numerical study of aerodynamic noise behaviors for a vertically-installed flat strut behind an asymmetrical airfoil.
European Journal of Mechanics - B/Fluids,
Vol. 88,
Issue. ,
p.
17.
Yang, Chenghao
Feng, Heying
Peng, Yehui
Tong, Fan
and
Bao, Nvzi
2022.
Numerical investigation of rod–airfoil interaction noise reduction using cylindrical collars.
The Journal of the Acoustical Society of America,
Vol. 151,
Issue. 6,
p.
3641.
Geyer, Thomas F.
2022.
Experimental Investigation of Flow and Noise Control by Porous Coated Tandem Cylinder Configurations.
AIAA Journal,
Vol. 60,
Issue. 7,
p.
4091.
Song, Kaiyao
Jin, Guoyong
Jia, Di
Hua, Runan
Ye, Tiangui
Sun, Zexi
and
Liu, Zhigang
2023.
Effects of viscoelastic fluid on noise reduction of the flow over a circular cylinder.
Journal of Fluids and Structures,
Vol. 122,
Issue. ,
p.
103976.
Li, Sen
He, Chuangxin
and
Liu, Yingzheng
2023.
Unsteady flow enhancement on an airfoil using sliding window weak-constraint four-dimensional variational data assimilation.
Physics of Fluids,
Vol. 35,
Issue. 6,
2023.
Applying reinforcement learning to mitigate wake-induced lift fluctuation of a wall-confined circular cylinder in tandem configuration.
Physics of Fluids,
Vol. 35,
Issue. 5,
Modi, Rishit
Alhawwary, Mohammad A.
Akbarzadeh, Amir
Witherden, Freddie
and
Jameson, Antony
2023.
Aeroacoustics noise prediction for the airfoil-rod benchmark using high-order large eddy simulation on unstructured grids and the acoustic analogy approach in frequency-domain.
Yu, Linqi
Yousif, Mustafa Z.
Lee, Young-Woo
Zhu, Xiaojue
Zhang, Meng
Kolesova, Paraskovia
and
Lim, Hee-Chang
2024.
Predicting unavailable parameters from existing velocity fields of turbulent flows using a GAN-based model.
Physical Review Fluids,
Vol. 9,
Issue. 2,
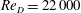 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathit{Re}}_D= 22\, 000$ and its reduction using single dielectric barrier discharge (SDBD) plasma actuators are simulated numerically both to confirm and extend experimental results. The numerical approach is based on large-eddy simulation (LES) for the turbulent flow field, a semi-empirical plasma actuation model, and Lighthill’s theory for acoustic calculation. Excellent agreement between LES and experimental results is obtained for both the baseline flow and flow with plasma control in terms of wake velocity profiles, turbulence intensity, and frequency spectra of pressure fluctuations on the downstream cylinder. The validated flow-field results allow an accurate acoustic analysis based on Lighthill’s equation, which is solved using a boundary-element method. The effectiveness of plasma actuators for reducing noise is clearly demonstrated. In the baseline flow, the acoustic field is dominated by the interaction between the downstream cylinder and the upstream wake. Through suppression of vortex shedding from the upstream cylinder, the interaction noise is reduced drastically by the plasma flow control, and the vortex-shedding noise from the downstream cylinder becomes equally important. At a free-stream Mach number of 0.2, the peak sound pressure level is reduced by approximately 16 dB. This suggests the viability of plasma actuation for active aeroacoustic control of airframe noise.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathit{Re}}_D= 22\, 000$ and its reduction using single dielectric barrier discharge (SDBD) plasma actuators are simulated numerically both to confirm and extend experimental results. The numerical approach is based on large-eddy simulation (LES) for the turbulent flow field, a semi-empirical plasma actuation model, and Lighthill’s theory for acoustic calculation. Excellent agreement between LES and experimental results is obtained for both the baseline flow and flow with plasma control in terms of wake velocity profiles, turbulence intensity, and frequency spectra of pressure fluctuations on the downstream cylinder. The validated flow-field results allow an accurate acoustic analysis based on Lighthill’s equation, which is solved using a boundary-element method. The effectiveness of plasma actuators for reducing noise is clearly demonstrated. In the baseline flow, the acoustic field is dominated by the interaction between the downstream cylinder and the upstream wake. Through suppression of vortex shedding from the upstream cylinder, the interaction noise is reduced drastically by the plasma flow control, and the vortex-shedding noise from the downstream cylinder becomes equally important. At a free-stream Mach number of 0.2, the peak sound pressure level is reduced by approximately 16 dB. This suggests the viability of plasma actuation for active aeroacoustic control of airframe noise.

