High-Reynolds-number steady currents of relatively dense fluid propagating along a horizontal boundary become unstable and mix with the overlying fluid if the gradient Richardson number across the interface is less than 1/4. The process of entrainment produces a deepening mixing layer at the interface, which increases the gradient Richardson number of this layer and eventually may suppress further entrainment. The conservation of the vertically averaged buoyancy and momentum flux, as the current advances along the boundary, leads to two integral constraints relating the downstream flow with that upstream of the mixing zone. These constraints are equivalent to imposing a Froude number in the upstream flow. Using the ansatz that the dowstream velocity and buoyancy profiles in the current have a lower well-mixed region overlain by an interfacial layer of constant gradient, we can use these two constraints to quantify the total entrainment of ambient fluid into the flow as a function of the gradient Richardson number of the downstream flow. This leads to recognition that both subcritical and supercritical currents may develop downstream of the mixing zone. However, as the mixing increases and the interfacial layer gradually deepens, there is a critical point at which these two solution branches coincide. For each upstream Froude number, we can also determine the downstream flow with maximal entrainment. This maximal entrainment solution coincides with the convergence point of the supercritical and subcritical branches. We compare this with the entrainment predicted for those solutions with a gradient Richardson number of 1/4, which corresponds to the marginally stable case. As the upstream Froude number 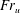$Fr_{u}$ increases, the maximum depth of the interfacial mixing layer gradually increases until eventually, for 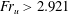$Fr_{u}>2.921$, the whole current may become modified through entrainment. We discuss the relevance of these results for mixing in gravity-driven flows.