Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T05:19:21.037Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-universal scaling transition of momentum cascade in wall turbulence

Published online by Cambridge University Press:  24 May 2019

Xi Chen Open the ORCID record for Xi Chen [Opens in a new window] ,
Fazle Hussain Open the ORCID record for Fazle Hussain [Opens in a new window]  and
Zhen-Su She Open the ORCID record for Zhen-Su She [Opens in a new window]
Xi Chen*
Affiliation:
Department of Mechanical Engineering, Texas Tech University, TX 79409, USA
Fazle Hussain*
Affiliation:
Department of Mechanical Engineering, Texas Tech University, TX 79409, USA
Zhen-Su She*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems and Department of Mechanics, College of Engineering, Peking University, Beijing 100871, China
*
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

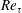As a counterpart of energy cascade, turbulent momentum cascade (TMC) in the wall-normal direction is important for understanding wall turbulence. Here, we report an analytic prediction of non-universal Reynolds number ($Re_{\unicode[STIX]{x1D70F}}$) scaling transition of the maximum TMC located at 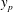$y_{p}$. We show that in viscous units, $y_{p}^{+}$ (and 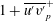$1+\overline{u^{\prime }v^{\prime }}_{p}^{+}$) displays a scaling transition from 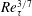$Re_{\unicode[STIX]{x1D70F}}^{3/7}$ (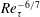$Re_{\unicode[STIX]{x1D70F}}^{-6/7}$) to 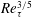$Re_{\unicode[STIX]{x1D70F}}^{3/5}$ (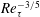$Re_{\unicode[STIX]{x1D70F}}^{-3/5}$) in turbulent boundary layer, in sharp contrast to that from $Re_{\unicode[STIX]{x1D70F}}^{1/3}$ (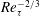$Re_{\unicode[STIX]{x1D70F}}^{-2/3}$) to $Re_{\unicode[STIX]{x1D70F}}^{1/2}$ (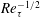$Re_{\unicode[STIX]{x1D70F}}^{-1/2}$) in a channel/pipe, countering the prevailing view of a single universal near-wall scaling. This scaling transition reflects different near-wall motions in the buffer layer for small 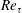$Re_{\unicode[STIX]{x1D70F}}$ and log layer for large 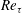$Re_{\unicode[STIX]{x1D70F}}$, with the non-universality being ascribed to the presence/absence of mean wall-normal velocity 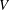$V$. Our predictions are validated by a large set of data, and a probable flow state with a full coupling between momentum and energy cascades beyond a critical 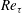$Re_{\unicode[STIX]{x1D70F}}$ is envisaged.

JFM classification

Turbulent Flows: Turbulence theory
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , R2
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahn, J., Lee, J. & Sung, H. J. 2017 Contribution of large-scale motions to the Reynolds shear stress in turbulent pipe flows. Intl J. Heat Fluid Flow 66, 209–216.10.1016/j.ijheatfluidflow.2017.06.009Google Scholar
Barenblatt, G. I. 1993 Scaling laws for fully developed turbulent shear flows. Part 1. Basic hypotheses and analysis. J. Fluid Mech. 248, 513–520.10.1017/S0022112093000874Google Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.10.1017/S0022112005004751Google Scholar
Chen, X., Hussain, F. & She, Z. S. 2018 Quantifying wall turbulence via a symmetry approach. Part 2. Reynolds stresses. J. Fluid Mech. 850, 401–438.10.1017/jfm.2018.405Google Scholar
Chen, X. & She, Z. S. 2016 Analytic prediction for planar turbulent boundary layers. Sci. China Phys. Mech. Astron. 59 (11), 114711.Google Scholar
Chen, X., Wei, B. B., Hussain, F. & She, Z. S. 2015 Anomalous dissipation and kinetic-energy distribution in pipes at very high Reynolds numbers. Phys. Rev. E 93, 011102(R).Google Scholar
Chin, C., Philip, J., Klewicki, J., Ooi, A. & Marusic, I. 2014 Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows. J. Fluid Mech. 757, 747–769.Google Scholar
Degraaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.10.1017/S0022112000001713Google Scholar
Fernholz, H. H. & Finleyt, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerospace 32, 245–311.10.1016/0376-0421(95)00007-0Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.10.1017/CBO9781139170666Google Scholar
Goldenfeld, N. 2006 Roughness-induced critical phenomena in a turbulent flow. Phys. Rev. Lett. 96, 044503.10.1103/PhysRevLett.96.044503Google Scholar
Goto, S. 2009 Turbulent energy cascade caused by vortex stretching. In Advances in Turbulence XII (ed. Eckhardt, B.), Springer Proceedings in Physics, vol. 132. Springer.Google Scholar
Hoyas, S. & Jimenez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.10.1063/1.2162185Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Iwamoto, K., Suzuki, Y. & Kasagi, N.2002 Database of fully developed channel flow. Tech. Rep. ILR-0201.Google Scholar
Jimenez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.10.1146/annurev-fluid-120710-101039Google Scholar
Jimenez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.Google Scholar
Kawata, T. & Alfredsson, P. H. 2018 Inverse interscale transport of the Reynolds shear stress in plane Couette turbulence. Phys. Rev. Lett. 120, 244501.Google Scholar
Klewicki, J. C. 2013 Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–621.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
L’vov, V. S., Procaccia, I. & Rudenko, O. 2008 Universal model of finite Reynolds number turbulent flow in channels and pipes. Phys. Rev. Lett. 100 (5), 054504.10.1103/PhysRevLett.100.054504Google Scholar
McKeon, B. J., Li, J., Jiang, W., Morrison, J. F. & Smits, A. J. 2004 Further observations on the mean velocity distribution in fully developed pipe flow. J. Fluid Mech. 501, 135–147.10.1017/S0022112003007304Google Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2007 Self-consistent high-Reynolds-number asymptotics for zero-pressure-gradient turbulent boundary layers. Phys. Fluids 19 (11), 115101.10.1063/1.2780196Google Scholar
Orlandi, P. & Leonardi, S.2007 Tech. Rep. WT-071016-URS-1. WALLTURB project.Google Scholar
Örlü, R.2009 Experimental studies in jet flows and zero pressure-gradient turbulent boundary layers. PhD thesis, KTH Royal Institute of Technology, Stockholm.Google Scholar
Schlatter, P., Li, Q., Brethouwer, G., Johansson, A. V. & Henningson, D. S. 2010 Simulations of spatially evolving turbulent boundary layers up to Re 𝜃 = 4300. Intl J. Heat Fluid Flow 31 (3), 251–261.10.1016/j.ijheatfluidflow.2009.12.011Google Scholar
She, Z. S., Chen, X. & Hussain, F. 2017 Quantifying wall turbulence via a symmetry approach: a Lie group theory. J. Fluid Mech. 827, 322–356.10.1017/jfm.2017.464Google Scholar
She, Z. S., Wu, Y., Chen, X. & Hussain, F. 2012 A multi-state description of roughness effects in turbulent pipe flow. New J. Phys. 14 (9), 093054.Google Scholar
She, Z. S., Zou, H.-Y., Xiao, M.-J., Chen, X. & Hussain, F. 2018 Prediction of compressible turbulent boundary layer via a symmetry-based length model. J. Fluid Mech. 857, 449–468.10.1017/jfm.2018.710Google Scholar
Sillero, J. A., Jimnez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 𝛿+ = 2000. Phys. Fluids 26 (10), 105109.Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to re 𝜃 = 1410. J. Fluid Mech. 187, 61–98.Google Scholar
Sreenivasan, K. R. 1988 Turbulence Management and Relaminarization. Springer.Google Scholar
Sreenivasan, K. R. 1999 Fluid turbulence. Rev. Mod. Phys. 71, S383–S395.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. Cambridge University Press.Google Scholar
Vallikivi, M., Ganapathisubramani, B. & Smits, A. J. 2015 Spectral scaling in boundary layers and pipes at very high Reynolds numbers. J. Fluid Mech. 771, 303–326.Google Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47 (1), 95–114.10.1146/annurev-fluid-010814-014637Google Scholar
Vincenti, P., Klewicki, J., Morrill-Winter, C., White, C. M. & Wosnik, M. 2013 Streamwise velocity statistics in turbulent boundary layers that spatially develop to high Reynolds number. Exp Fluids 54, 1629.Google Scholar
Wei, T. 2018 Integral properties of turbulent-kinetic-energy production and dissipation in turbulent wall-bounded flows. J. Fluid Mech. 854, 449–473.Google Scholar
Wei, T., Fife, P., Klewicki, J. & Mcmurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.Google Scholar
Wei, T. & Klewicki, J. 2016 Scaling properties of the mean wall-normal velocity in zero-pressure-gradient boundary layers. Phys. Rev. Fluids 1, 082401(R).10.1103/PhysRevFluids.1.082401Google Scholar
Wu, X. H. & Moin, P. 2008 Direct numerical simulation on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 608, 5–41.Google Scholar
Wu, X. H. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.10.1017/S0022112009006624Google Scholar
Yakhot, V. & Donzis, D. 2017 Emergence of multiscaling in a random-force stirred fluid. Phys. Rev. Lett. 119, 044501.Google Scholar
Yamamoto, Y. & Tsuji, Y. 2018 Numerical evidence of logarithmic regions in channel flow at Re 𝜏 = 8000. Phys. Rev. Fluids 3, 012602.Google Scholar
Yang, X. I. A. & Lozano-Durán, A. 2017 A multifractal model for the momentum transfer process in wall-bounded flows. J. Fluid Mech. 824, R2.10.1017/jfm.2017.406Google Scholar
Yao, J., Chen, X. & Hussain, F. 2018 Drag control in wall-bounded turbulent flows via spanwise opposed wall-jet forcing. J. Fluid Mech. 852, 678–709.10.1017/jfm.2018.553Google Scholar