Article contents
Non-Newtonian slender drops in a nonlinear extensional flow
Published online by Cambridge University Press: 27 August 2019
Abstract
In this theoretical report we explore the deformation and stability of a power-law non-Newtonian slender drop embedded in a Newtonian liquid undergoing a nonlinear extensional creeping flow. The dimensionless parameters describing this problem are: the capillary number 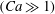 $(Ca\gg 1)$, the viscosity ratio
$(Ca\gg 1)$, the viscosity ratio 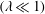 $(\unicode[STIX]{x1D706}\ll 1)$, the power-law index
$(\unicode[STIX]{x1D706}\ll 1)$, the power-law index 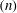 $(n)$ and the nonlinear intensity of the flow
$(n)$ and the nonlinear intensity of the flow  $(|E|\ll 1)$. Asymptotic analytical solutions were obtained near the centre and close to the end of the drop suggesting that only Newtonian and shear thinning drops
$(|E|\ll 1)$. Asymptotic analytical solutions were obtained near the centre and close to the end of the drop suggesting that only Newtonian and shear thinning drops 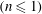 $(n\leqslant 1)$ with pointed ends are possible. We described the shape of the drop as a series expansion about the centre of the drop, and performed a stability analysis in order to distinguish between stable and unstable stationary states and to establish the breakup point. Our findings suggest: (i) shear thinning drops are less elongated than Newtonian drops, (ii) as non-Newtonian effects increase or as
$(n\leqslant 1)$ with pointed ends are possible. We described the shape of the drop as a series expansion about the centre of the drop, and performed a stability analysis in order to distinguish between stable and unstable stationary states and to establish the breakup point. Our findings suggest: (i) shear thinning drops are less elongated than Newtonian drops, (ii) as non-Newtonian effects increase or as  $n$ decreases, breakup becomes more difficult, and (iii) as the flow becomes more nonlinear, breakup is facilitated.
$n$ decreases, breakup becomes more difficult, and (iii) as the flow becomes more nonlinear, breakup is facilitated.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 4
- Cited by


