Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T14:40:37.847Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-modal stability analysis of miscible viscous fingering with non-monotonic viscosity profiles

Published online by Cambridge University Press:  12 October 2018

Tapan Kumar Hota  and
Manoranjan Mishra Open the ORCID record for Manoranjan Mishra [Opens in a new window]
Tapan Kumar Hota
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, 140001 Rupnagar, India
Manoranjan Mishra*
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, 140001 Rupnagar, India Department of Chemical Engineering, Indian Institute of Technology Ropar, 140001 Rupnagar, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A non-modal linear stability analysis (NMA) of the miscible viscous fingering in a porous medium is studied for a toy model of non-monotonic viscosity variation. The onset of instability and its physical mechanism are captured in terms of the singular values of the propagator matrix corresponding to the non-autonomous linear equations. We discuss two types of non-monotonic viscosity profiles, namely, with unfavourable (when a less viscous fluid displaces a high viscous fluid) and with favourable (when a more viscous fluid displaces a less viscous fluid) endpoint viscosities. A linear stability analysis yields instabilities for such viscosity variations. Using the optimal perturbation structure, we are able to show that an initially unconditional stable state becomes unstable corresponding to the most unstable initial disturbance. In addition, we also show that to understand the spatio-temporal evolution of the perturbations it is necessary to analyse the viscosity gradient with respect to the concentration and the location of the maximum concentration 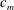$c_{m}$. For the favourable endpoint viscosities, a weak transient instability is observed when the viscosity maximum moves close to the pure invading or defending fluid. This instability is attributed to an interplay between the sharp viscosity gradient and the favourable endpoint viscosity contrast. Further, the usefulness of the non-modal analysis demonstrating the physical mechanism of the quadruple structure of the perturbations from the optimal concentration disturbances is discussed. We demonstrate the dissimilarity between the quasi-steady-state approach and NMA in finding the correct perturbation structure and the onset, for both the favourable and unfavourable viscosity profiles. The correctness of the linear perturbation structure obtained from the non-modal stability analysis is validated through nonlinear simulations. We have found that the nonlinear simulations and NMA results are in good agreement. In summary, a non-monotonic variation of the viscosity of a miscible fluid pair is seen to have a larger influence on the onset of fingering instabilities than the corresponding Arrhenius type relationship.

JFM classification

Interfacial Flows (free surface): Fingering instability Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 552 - 579
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bacri, J. C., Rakotomalala, N., Dalin, D. & Wouméni, R. 1992a Miscible viscous fingering: experiments versus continuum approach. Phys. Fluids A 4, 1611–1619.Google Scholar
Bacri, J. C., Salin, D. & Yortsos, Y. 1992b Analyse linéaire de la stabilité de l’écoulement de fluides miscibles en milieux poreux. C. R. Acad. Sci. Paris 314, 139–144.Google Scholar
Bayada, G. & Chambat, M. 1986 The transition between the Stokes equations and the Reynolds equation: a mathematical proof. Appl Maths Optim. 14, 73–93.Google Scholar
Ben, Y., Demekhin, E. A. & Chang, H. C. 2002 A spectral theory for small amplitude miscible fingering. Phys. Fluids 14, 999–1010.Google Scholar
Bhatia, R. 1997 Matrix Analysis, Graduate Texts in Mathematics, vol. 169. Springer.Google Scholar
Blunt, M. J. & Christie, M. A.1991 Exact solutions for viscous fingering in two-phase, three-component flow. Paper SPE 22613, presented at the 66th Annual Technical Conference and Exhibition of the Society of Petroleum Engineers, Dallas, TX, 6–9 October 1991.Google Scholar
Chang, H. C., Demekhin, E. A. & Kalaidin, E. 1998 Generation and suppression of radiation by solitary pulses. Soc. Ind. Appl. Maths J. Appl. Maths 58, 1246–1277.Google Scholar
Chikhliwala, E. D., Huang, A. B. & Yortsos, Y. C. 1998 Numerical study of the linear stability of immiscible displacement in porous media. Trans. Porous Med. 3, 257–276.Google Scholar
Dastvareh, B & Azaiez, J. 2017 Instabilities of nanofluid flow displacements in porous media. Phys. Fluids 29, 044101.Google Scholar
Haudin, F., Callewaert, M., De Malsche, W. & De Wit, A. 2016 Influence of nonideal mixing properties on viscous fingering in micropillar array columns. Phys. Rev. Fluids 1, 074001.Google Scholar
Hejazi, S. H., Trevelyan, P. M. J., Azaiez, J. & De Wit, A. 2010 Viscous fingering of a miscible reactive A+B→C interface: a linear stability analysis. J. Fluid Mech. 652, 501–528.Google Scholar
Hickernell, J. F. & Yortsos, Y. C. 1986 Linear stability of miscible displacement processes in porous media in the absence of dispersion. Stud. Appl. Maths 74 (2), 93–115.Google Scholar
Homsy, G. M. 1987 Viscous fingering in porous media. Annu. Rev. Fluid Mech. 19, 271–311.Google Scholar
Hota, T. K., Pramanik, S. & Mishra, M. 2015a Non-modal linear stability analysis of miscible viscous fingering in a Hele-Shaw cell. Phys. Rev. E 92, 053007.Google Scholar
Hota, T. K., Pramanik, S. & Mishra, M. 2015b Onset of fingering instability in a finite slice of adsorbed solute. Phys. Rev. E 92, 023013.Google Scholar
Kim, M. C. 2012 Linear stability analysis on the onset of the viscous fingering of a miscible slice in a porous media. Adv. Water Resour. 35, 1–9.Google Scholar
Kim, M. C. & Choi, C. K. 2011 The stability of miscible displacement in porous media: nonmonotonic viscosity profiles. Phys. Fluids 23, 084105.Google Scholar
Kumar, S. & Homsy, G. M. 1999 Direct numerical simulation of hydrodynamic instabilities in two- and three-dimensional viscoelastic free shear layers. J. Non-Newtonian Fluid Mech. 83, 249–276.Google Scholar
Latil, M. 1980 Enhanced Oil Recovery. Gulf Publishing Co. Google Scholar
Manickam, O. & Homsy, G. M. 1993 Stability of miscible displacements in porous media with nonmonotonic viscosity profiles. Phys. Fluids A 5, 1356–1367.Google Scholar
Manickam, O. & Homsy, G. M. 1994 Simulation of viscous fingering in miscible displacements with nonmonotonic viscosity profiles. Phys. Fluids 6, 95–107.Google Scholar
Mishra, M., Trevelyan, P. M. J., Almarcha, C. & De Wit, A. 2010 Influence of double diffusive effects on miscible viscous fingering. Phys. Rev. Lett. 105, 204501.Google Scholar
Nagatsu, Y. & De Wit, A. 2011 Viscous fingering of a miscible reactive A + B → C interface for an infinitely fast chemical reaction: nonlinear simulations. Phys. Fluids 23, 043102.Google Scholar
Nagatsu, Y., Ishii, Y., Tada, Y. & De Wit, A. 2014 Hydrodynamic fingering instability induced by a precipitation reaction. Phys. Rev. Lett. 113, 024502.Google Scholar
Nazarov, S. A. 1990 Asymptotic solution of the Navier–Stokes problem on the flow in thin layer fluid. Siber. Math. J. 31, 296–307.Google Scholar
Nield, D. A. & Bejan, A. 1992 Convection in Porous Media, 2nd edn. Springer.Google Scholar
Pankiewitz, C. & Meiburg, E. 1999 Miscible porous media displacements in the quarter five-spot configuration. Part 3. Non-monotonic viscosity profiles. J. Fluid Mech. 388, 171–195.Google Scholar
Pego, R. L. & Weinstein, M. I. 1994 Asymptotic stability of solitary waves. Commun. Math. Phys. 164, 305–349.Google Scholar
Pramanik, S., Hota, T. K. & Mishra, M. 2015 Influence of viscosity contrast on buoyantly unstable miscible fluids in porous media. J. Fluid Mech. 780, 388–406.Google Scholar
Pramanik, S. & Mishra, M. 2013 Linear stability analysis of Korteweg stresses effect on the miscible viscous fingering in porous media. Phys. Fluids 25, 074104.Google Scholar
Pritchard, D. 2009 The linear stability of double-diffusive miscible rectilinear displacements in a Hele-Shaw cell. Eur. J. Mech. (B/Fluids) 28, 564–577.Google Scholar
Rapaka, S., Chen, S., Pawar, R. J., Stauffer, P. H. & Zhang, D. 2008 Non-modal growth of perturbations in density-driven convection in porous media. J. Fluid Mech. 609, 285–303.Google Scholar
Riolfo, L. A., Nagatsu, Y., Iwata, S., Maes, R., Trevelyan, P. M. J. & De Wit, A. 2012 Experimental evidence of reaction-driven miscible viscous fingering. Phys. Rev. E 85, 015304(R).Google Scholar
Saffman, P. G. & Taylor, G. 1958 The penetration of a fluid into a medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245, 312–329.Google Scholar
Schafroth, D., Goyal, N. & Meiburg, E. 2007 Miscible displacements in Hele-Shaw cells: nonmonotonic viscosity profiles. Eur. J. Mech. (B/Fluids) 26, 444–453.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Tan, C. T. & Homsy, G. M. 1986 Stability of miscible displacements in porous media: rectilinear flow. Phys. Fluids 29, 3549–3556.Google Scholar
Tan, C. T. & Homsy, G. M. 1988 Simulation of non-linear viscous fingering in miscible displacement. Phys. Fluids 31, 1330–1338.Google Scholar
Vidyasagar, M. 2002 Nonlinear Systems Analysis, 2nd edn. Prentice Hall.Google Scholar
Wang, L.-C.2014 Studies on flow instabilities on the miscible fluid interface in a Hele-Shaw cell-injection and lifting. PhD thesis, National Chiao Tung University, Taiwan.Google Scholar
Weast, R. C. 1990 Handbook of Chemistry and Physics. CRC.Google Scholar
Zick, A. A. & Homsy, G. M. 1982 Stokes flow through periodic arrays of spheres. J. Fluid Mech. 115, 13–26.Google Scholar