Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T10:25:49.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear interactions between an unstably stratified shear flow and a phase boundary

Published online by Cambridge University Press:  27 May 2021

S. Toppaladoddi Open the ORCID record for S. Toppaladoddi [Opens in a new window]
S. Toppaladoddi*
Affiliation:
All Souls College, OxfordOX1 4AL, UK Department of Physics, University of Oxford, OxfordOX1 3PU, UK Mathematical Institute, University of Oxford, OxfordOX2 6GG, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

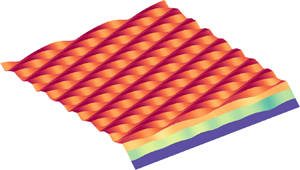
Well-resolved numerical simulations are used to study Rayleigh–Bénard–Poiseuille flow over an evolving phase boundary for moderate values of Péclet ($Pe \in [0, 50]$) and Rayleigh ($Ra \in [2.15 \times 10^3, 10^6]$) numbers. The relative effects of mean shear and buoyancy are quantified using a bulk Richardson number: $Ri_b = Ra \cdot Pr/Pe^2 \in [8.6 \times 10^{-1}, 10^4]$, where $Pr$ is the Prandtl number. For $Ri_b = O(1)$, we find that the Poiseuille flow inhibits convective motions, resulting in the heat transport being only due to conduction and, for $Ri_b \gg 1$, the flow properties and heat transport closely correspond to the purely convective case. We also find that for certain $Ra$ and $Pe$, such that $Ri_b \in [15,95]$, there is a pattern competition for convection cells with a preferred aspect ratio. Furthermore, we find travelling waves at the solid–liquid interface when $Pe \neq ~0$, in qualitative agreement with other sheared convective flows in the experiments of Gilpin et al. (J. Fluid Mech., vol. 99(3), 1980, pp. 619–640) and the linear stability analysis of Toppaladoddi & Wettlaufer (J. Fluid Mech., vol. 868, 2019, pp. 648–665).

JFM classification

Phase change: Solidification/melting
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 919 , 25 July 2021 , A28
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Benzi, R., Succi, S. & Vergassola, M. 1992 The lattice Boltzmann equation: theory and applications. Phys. Rep. 222 (3), 145–197.CrossRefGoogle Scholar
Bushuk, M., Holland, D.M., Stanton, T.P., Stern, A. & Gray, C. 2019 Ice scallops: a laboratory investigation of the ice–water interface. J. Fluid Mech. 873, 942–976.CrossRefGoogle ScholarPubMed
Chandrasekhar, S. 2013 Hydrodynamic and Hydromagnetic Stability. Dover Publications.Google Scholar
Chen, S. & Doolen, G.D. 1998 Lattice Boltzmann method for fluid flows. Ann. Rev. Fluid Mech. 30 (1), 329–364.CrossRefGoogle Scholar
Ciliberto, S. & Gollub, J.P. 1984 Pattern competition leads to chaos. Phys. Rev. Lett. 52 (11), 922–925.CrossRefGoogle Scholar
Coriell, S.R., McFadden, G.B., Boisvert, R.F. & Sekerka, R.F. 1984 Effect of a forced couette flow on coupled convective and morphological instabilities during unidirectional solidification. J. Cryst. Growth 69 (1), 15–22.CrossRefGoogle Scholar
Couston, L.-A., Hester, E., Favier, B., Taylor, J.R., Holland, P.R. & Jenkins, A. 2020 Topography generation by melting and freezing in a turbulent shear flow. J. Fluid Mech. 911, A44.CrossRefGoogle Scholar
Davies Wykes, M.S., Huang, J.M., Hajjar, G.A. & Ristroph, L. 2018 Self-sculpting of a dissolvable body due to gravitational convection. Phys. Rev. Fluids 3 (4), 043801.CrossRefGoogle Scholar
Davis, S.H., Müller, U. & Dietsche, C. 1984 Pattern selection in single-component systems coupling Bénard convection and solidification. J. Fluid Mech. 144, 133–151.CrossRefGoogle Scholar
Delves, R.T. 1968 Theory of stability of a solid-liquid interface during growth from stirred melts. J. Cryst. Growth 3, 562–568.CrossRefGoogle Scholar
Delves, R.T. 1971 Theory of the stability of a solid-liquid interface during growth from stirred melts II. J. Cryst. Growth 8 (1), 13–25.CrossRefGoogle Scholar
Dietsche, C. & Müller, U. 1985 Influence of Bénard convection on solid–liquid interfaces. J. Fluid Mech. 161, 249–268.CrossRefGoogle Scholar
Epstein, M. & Cheung, F.B. 1983 Complex freezing-melting interfaces in fluid flow. Annu. Rev. Fluid Mech. 15 (1), 293–319.CrossRefGoogle Scholar
Esfahani, B.R., Hirata, S.C., Berti, S. & Calzavarini, E. 2018 Basal melting driven by turbulent thermal convection. Phys. Rev. Fluids 3 (5), 053501.CrossRefGoogle Scholar
Favier, B., Purseed, J. & Duchemin, L. 2019 Rayleigh–Bénard convection with a melting boundary. J. Fluid Mech. 858, 437–473.CrossRefGoogle Scholar
Feltham, D.L. & Worster, M.G. 1999 Flow-induced morphological instability of a mushy layer. J. Fluid Mech. 391, 337–357.CrossRefGoogle Scholar
Forth, S.A. & Wheeler, A.A. 1989 Hydrodynamic and morphological stability of the unidirectional solidification of a freezing binary alloy: a simple model. J. Fluid Mech. 202, 339–366.CrossRefGoogle Scholar
Gilpin, R.R., Hirata, T. & Cheng, K.C. 1980 Wave formation and heat transfer at an ice-water interface in the presence of a turbulent flow. J. Fluid Mech. 99 (3), 619–640.CrossRefGoogle Scholar
Glazier, J.A., Segawa, T., Naert, A. & Sano, M. 1999 Evidence against ‘ultrahard'thermal turbulence at very high Rayleigh numbers. Nature 398 (6725), 307–310.CrossRefGoogle Scholar
Glicksman, M.E., Coriell, S.R. & McFadden, G.B. 1986 Interaction of flows with the crystal-melt interface. Annu. Rev. Fluid Mech. 18 (1), 307–335.CrossRefGoogle Scholar
Hewitt, I.J. 2020 Subglacial plumes. Annu. Rev. Fluid Mech. 52, 145–169.CrossRefGoogle Scholar
Hirata, T., Gilpin, R.R. & Cheng, K.C. 1979 a The steady state ice layer profile on a constant temperature plate in a forced convection flow—II. The transition and turbulent regimes. Intl J. Heat Mass Transfer 22 (10), 1435–1443.CrossRefGoogle Scholar
Hirata, T., Gilpin, R.R., Cheng, K.C. & Gates, E.M. 1979 b The steady state ice layer profile on a constant temperature plate in a forced convection flow—I. Laminar regime. Intl J. Heat Mass Transfer 22 (10), 1425–1433.CrossRefGoogle Scholar
Huber, C., Parmigiani, A., Chopard, B., Manga, M. & Bachmann, O. 2008 Lattice Boltzmann model for melting with natural convection. Intl J. Heat Fluid Flow 29 (5), 1469–1480.CrossRefGoogle Scholar
Huppert, H.E. 1986 Intrusion of fluid mechanics into geology. J. Fluid Mech. 173, 557–594.CrossRefGoogle Scholar
Jiaung, W.-S., Ho, J.-R. & Kuo, C.-P. 2001 Lattice Boltzmann method for the heat conduction problem with phase change. Numer. Heat Transfer B 39 (2), 167–187.Google Scholar
Johnston, H. & Doering, C.R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102, 064501.CrossRefGoogle ScholarPubMed
Landau, L.D. & Lifshitz, E.M. 2013 Fluid Mechanics. Elsevier.Google Scholar
Latt, J. 2007 Hydrodynamic limit of lattice Boltzmann equations. PhD thesis, Université de Genève.Google Scholar
Maykut, G.A. & Untersteiner, N. 1971 Some results from a time-dependent thermodynamic model of sea ice. J. Geophys. Res. 76 (6), 1550–1575.CrossRefGoogle Scholar
Monin, A.S. & Yaglom, A.M. 1971 Statistical Fluid Mechanics: Mechanics of Turbulence Volume 1. Dover Publications.Google Scholar
Neufeld, J.A. & Wettlaufer, J.S. 2008 a An experimental study of shear-enhanced convection in a mushy layer. J. Fluid Mech. 612, 363–385.CrossRefGoogle Scholar
Neufeld, J.A. & Wettlaufer, J.S. 2008 b Shear-enhanced convection in a mushy layer. J. Fluid Mech. 612, 339–361.CrossRefGoogle Scholar
Purseed, J., Favier, B., Duchemin, L. & Hester, E.W. 2020 Bistability in Rayleigh-Bénard convection with a melting boundary. Phys. Rev. Fluids 5 (2), 023501.CrossRefGoogle Scholar
Ramudu, E., Hirsh, B.H., Olson, P. & Gnanadesikan, A. 2016 Turbulent heat exchange between water and ice at an evolving ice–water interface. J. Fluid Mech. 798, 572–597.CrossRefGoogle Scholar
Sel'Kov, E.E. 1968 Self-oscillations in glycolysis 1. A simple kinetic model. Eur. J. Biochem. 4 (1), 79–86.CrossRefGoogle ScholarPubMed
Strogatz, S.H. 2018 Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. CRC Press.CrossRefGoogle Scholar
Succi, S. 2001 The Lattice-Boltzmann Equation. Oxford University Press.Google Scholar
Toppaladoddi, S. 2017 The staistical physics, fluid mechanics, and the climatology of Arctic sea ice. PhD thesis, Yale University.Google Scholar
Toppaladoddi, S., Succi, S. & Wettlaufer, J.S. 2015 a Tailoring boundary geometry to optimize heat transport in turbulent convection. EPL 111 (4), 44005.CrossRefGoogle Scholar
Toppaladoddi, S., Succi, S. & Wettlaufer, J.S. 2015 b Turbulent transport processes at rough surfaces with geophysical applications. Procedia IUTAM 15, 34–40.CrossRefGoogle Scholar
Toppaladoddi, S. & Wettlaufer, J.S. 2019 The combined effects of shear and buoyancy on phase boundary stability. J. Fluid Mech. 868, 648–665.CrossRefGoogle Scholar
Voller, V. & Cross, M. 1981 Accurate solutions of moving boundary problems using the enthalpy method. Intl J. Heat Mass Transfer 24 (3), 545–556.CrossRefGoogle Scholar
Voller, V.R., Cross, M. & Markatos, N.C. 1987 An enthalpy method for convection/diffusion phase change. Intl J. Numer. Meth. Engng 24 (1), 271–284.CrossRefGoogle Scholar
Waleffe, F., Boonkasame, A. & Smith, L.M. 2015 Heat transport by coherent Rayleigh-Bénard convection. Phys. Fluids 27 (5), 051702.CrossRefGoogle Scholar
Wettlaufer, J.S., Worster, M.G. & Huppert, H.E. 1997 Natural convection during solidification of an alloy from above with application to the evolution of sea ice. J. Fluid Mech. 344, 291–316.CrossRefGoogle Scholar
Worster, M.G. 1997 Convection in mushy layers. Annu. Rev. Fluid Mech. 29 (1), 91–122.CrossRefGoogle Scholar
Worster, M.G. 2000 Solidification of fluids. In Perspectives in Fluid Dynamics — A Collective Introduction to Current Research (ed. G.K. Batchelor, H.K. Moffatt & M.G. Worster), pp. 393–446. Cambridge University Press.Google Scholar

Toppaladoddi et al. supplementary movie 1

See pdf file for movie caption

Download Toppaladoddi et al. supplementary movie 1(Video)
Video 18.3 MB

Toppaladoddi et al. supplementary movie 2

See pdf file for movie caption

Download Toppaladoddi et al. supplementary movie 2(Video)
Video 17.3 MB