Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-09T14:36:31.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear behaviour of convergent Richtmyer–Meshkov instability

Published online by Cambridge University Press:  19 August 2019

Xisheng Luo Open the ORCID record for Xisheng Luo [Opens in a new window] ,
Ming Li ,
Juchun Ding Open the ORCID record for Juchun Ding [Opens in a new window] ,
Zhigang Zhai Open the ORCID record for Zhigang Zhai [Opens in a new window]  and
Ting Si Open the ORCID record for Ting Si [Opens in a new window]
Xisheng Luo
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Ming Li
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Juchun Ding*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Zhigang Zhai
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Ting Si
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A novel shock tube is designed to investigate the nonlinear feature of convergent Richtmyer–Meshkov instability on a single-mode interface formed by a soap film technique. The shock tube employs a concave–oblique–convex wall profile which first transforms a planar shock into a cylindrical arc, then gradually strengthens the cylindrical shock along the oblique wall, and finally converts it back into a planar one. Therefore, the new facility can realize analysis on compressibility and nonlinearity of convergent Richtmyer–Meshkov instability by eliminating the interface deceleration and reshock. 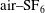Five sinusoidal $\text{air}{-}\text{SF}_{6}$ interfaces with different amplitudes and wavelengths are considered. For all cases, the perturbation amplitude experiences a linear growth much longer than that in the planar geometry. A compressible linear model is derived by considering a constant uniform fluid compression, which shows a slight difference to the incompressible theory. However, both the linear models overestimate the perturbation growth from a very early stage due to the presence of strong nonlinearity. The nonlinear model of Wang et al. (Phys. Plasmas, vol. 22, 2015, 082702) is demonstrated to predict well the amplitude growth up to a normalized time of 1.0. The prolongation of the linear increment is mainly ascribed to the counteraction between the promotion by geometric convergence and the suppression by nonlinearity. Growths of the first three harmonics, obtained by a Fourier analysis of the interface contour, provide a first thorough validation of the nonlinear theory.

JFM classification

Instability: Nonlinear instability Compressible Flows: Shock waves Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 877 , 25 October 2019 , pp. 130 - 141
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bell, G. I.1951 Taylor instability on cylinders and spheres in the small amplitude approximation. In Los Alamos National Laboratory, Los Alamos, NM, Report LA, vol. 1321.Google Scholar
Biamino, L., Jourdan, G., Mariani, C., Houas, L., Vandenboomgaerde, M. & Souffland, D. 2015 On the possibility of studying the converging Richtmyer–Meshkov instability in a conventional shock tube. Exp. Fluids 56 (2), 1–5.Google Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.10.1146/annurev.fluid.34.090101.162238Google Scholar
Ding, J., Si, T., Yang, J., Lu, X., Zhai, Z. & Luo, X. 2017 Measurement of a Richtmyer–Meshkov instability at an air–F6 interface in a semiannular shock tube. Phys. Rev. Lett. 119 (1), 014501.10.1103/PhysRevLett.119.014501Google Scholar
Dumitrescu, L. Z. 1992 On efficient shock-focusing configurations. In 11th Australasian Fluid Mechanics Conference, Univ. of Tasmania, Hobart, Australia, pp. 723–725.Google Scholar
Epstein, R. 2004 On the Bell–Plesset effects: the effects of uniform compression and geometrical convergence on the classical Rayleigh–Taylor instability. Phys. Plasmas 11 (11), 5114–5124.10.1063/1.1790496Google Scholar
Fincke, J. R., Lanier, N. E., Batha, S. H., Hueckstaedt, R. M., Magelssen, G. R., Rothman, S. D., Parker, K. W. & Horsfield, C. J. 2005 Effect of convergence on growth of the Richtmyer–Meshkov instability. Laser Part. Beams 23 (01), 21–25.10.1017/S0263034605050068Google Scholar
Hosseini, S. H. R. & Takayama, K. 2005 Experimental study of Richtmyer–Meshkov instability induced by cylindrical shock waves. Phys. Fluids 17, 084101.10.1063/1.1964916Google Scholar
Jacobs, J. W. & Krivets, V. V. 2005 Experiments on the late-time development of single-mode Richtmyer–Meshkov instability. Phys. Fluids 17, 034105.10.1063/1.1852574Google Scholar
Lanier, N. E., Barnes, C. W., Batha, S. H., Day, R. D., Magelssen, G. R., Scott, J. M., Dunne, A. M., Parker, K. W. & Rothman, S. D. 2003 Multimode seeded Richtmyer–Meshkov mixing in a convergent, compressible, miscible plasma system. Phys. Plasmas 10, 1816–1821.10.1063/1.1542886Google Scholar
Lei, F., Ding, J., Si, T., Zhai, Z. & Luo, X. 2017 Experimental study on a sinusoidal air/SF6 interface accelerated by a cylindrically converging shock. J. Fluid Mech. 826, 819–829.10.1017/jfm.2017.506Google Scholar
Lindl, J., Landen, O., Edwards, J., Moses, E. & Team, N. 2014 Review of the national ignition campaign 2009–2012. Phys. Plasmas 21, 020501.10.1063/1.4865400Google Scholar
Liu, W. H., He, X. T. & Yu, C. P. 2012 Cylindrical effects on Richtmyer–Meshkov instability for arbitrary Atwood numbers in weakly nonlinear regime. Phys. Plasmas 19, 072108.Google Scholar
Liu, L., Liang, Y., Ding, J., Liu, N. & Luo, X. 2018 An elaborate experiment on the single-mode Richtmyer–Meshkov instability. J. Fluid Mech. 853, R2.10.1017/jfm.2018.628Google Scholar
Liu, W. H., Yu, C. P., Ye, W. H., Wang, L. F. & He, X. T. 2014 Nonlinear theory of classical cylindrical Richtmyer–Meshkov instability for arbitrary Atwood numbers. Phys. Plasmas 21, 062119.Google Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2014 Turbulent mixing driven by spherical implosions. Part 1. Flow description and mixing-layer growth. J. Fluid Mech. 748, 85–112.10.1017/jfm.2014.161Google Scholar
Luo, X., Ding, J., Wang, M., Zhai, Z. & Si, T. 2015 A semi-annular shock tube for studying cylindrically converging Richtmyer–Meshkov instability. Phys. Fluids 27 (9), 091702.10.1063/1.4931929Google Scholar
Luo, X., Wang, X. & Si, T. 2013 The Richtmyer–Meshkov instability of a three-dimensional air/SF6 interface with a minimum-surface feature. J. Fluid Mech. 722, R2.10.1017/jfm.2013.148Google Scholar
Luo, X., Zhang, F., Ding, J., Si, T., Yang, J., Zhai, Z. & Wen, C. 2018 Long-term effect of Rayleigh–Taylor stabilization on converging Richtmyer–Meshkov instability. J. Fluid Mech. 849, 231–244.10.1017/jfm.2018.424Google Scholar
Matsuoka, C. & Nishihara, K. 2006 Fully nonlinear evolution of a cylindrical vortex sheet in incompressible Richtmyer–Meshkov instabilitys. Phys. Rev. E 73, 055304.Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4, 101–104.Google Scholar
Plesset, M. S. 1954 On the stability of fluid flows with spherical symmetry. J. Appl. Phys. 25, 96–98.10.1063/1.1721529Google Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock-bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.10.1146/annurev-fluid-122109-160744Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.10.1002/cpa.3160130207Google Scholar
Si, T., Long, T., Zhai, Z. & Luo, X. 2015 Experimental investigation of cylindrical converging shock waves interacting with a polygonal heavy gas cylinder. J. Fluid Mech. 784, 225–251.10.1017/jfm.2015.581Google Scholar
Si, T., Zhai, Z. & Luo, X. 2014 Experimental study of Richtmyer–Meshkov instability in a cylindrical converging shock tube. Laser Part. Beams 32, 343–351.10.1017/S0263034614000202Google Scholar
Vandenboomgaerde, M., Rouzier, P., Souffland, D., Biamino, L., Jourdan, G., Houas, L. & Mariani, C. 2018 Nonlinear growth of the converging Richtmyer–Meshkov instability in a conventional shock tube. Phys. Rev. Fluids 3, 014001.10.1103/PhysRevFluids.3.014001Google Scholar
Vandenboomgaerde, M., Souffland, D., Mariani, C., Biamino, L., Jourdan, G. & Houas, L. 2014 An experimental and numerical investigation of the dependency on the initial conditions of the Richtmyer–Meshkov instability. Phys. Fluids 26 (2), 024109.10.1063/1.4865836Google Scholar
Wang, L. F., Wu, J. F., Guo, H. Y., Ye, W. H., Liu, J., Zhang, W. Y. & He, X. T. 2015 Weakly nonlinear Bell–Plesset effects for a uniformly converging cylinder. Phys. Plasmas 22, 082702.Google Scholar
Zhai, Z., Liu, C., Qin, F., Yang, J. & Luo, X. 2010 Generation of cylindrical converging shock waves based on shock dynamics theory. Phys. Fluids 22, 041701.10.1063/1.3392603Google Scholar
Zhai, Z., Zou, L., Wu, Q. & Luo, X. 2018 Review of experimental Richtmyer–Meshkov instability in shock tube: from simple to complex. Proc. Inst. Mech. Engrs Part C 232 (16), 2830–2849.10.1177/0954406217727305Google Scholar
Zhan, D., Li, Z., Yang, J., Zhu, Y. & Yang, J. 2018 Note: A contraction channel design for planar shock wave enhancement. Rev. Sci. Instrum. 89, 056104.Google Scholar
Zhou, Y. 2017 Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 720–722, 1–136.Google Scholar