Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-07T08:04:19.817Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-invasive measurement of the pressure distribution in a deformable micro-channel

Published online by Cambridge University Press:  07 October 2013

Ozgur Ozsun ,
Victor Yakhot  and
Kamil L. Ekinci
Ozgur Ozsun
Affiliation:
Department of Mechanical Engineering, Boston University, Boston, MA 02215, USA
Victor Yakhot
Affiliation:
Department of Mechanical Engineering, Boston University, Boston, MA 02215, USA
Kamil L. Ekinci*
Affiliation:
Department of Mechanical Engineering, Boston University, Boston, MA 02215, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct and non-invasive measurement of the pressure distribution in test sections of a micro-channel is a challenging, if not an impossible, task. Here, we present an analytical method for extracting the pressure distribution in a deformable micro-channel under flow. Our method is based on a measurement of the channel deflection profile as a function of applied hydrostatic pressure; this initial measurement generates ‘constitutive curves’ for the deformable channel. The deflection profile under flow is then matched to the constitutive curves, providing the hydrodynamic pressure distribution. The method is validated by measurements on planar microfluidic channels against analytic and numerical models. 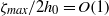The accuracy here is independent of the nature of the wall deformations and is not degraded even in the limit of large deflections, ${\zeta }_{max} / 2{h}_{0} = O(1)$, with 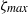${\zeta }_{max} $ and 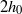$2{h}_{0} $ being the maximum deflection and the unperturbed height of the channel, respectively. We discuss possible applications of the method in characterizing micro-flows, including those in biological systems.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Micro-/Nano-fluid dynamics: Microfluidics
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 734 , 10 November 2013 , R1
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akbarian, M., Faivre, M. & Stone, H. A. 2006 High-speed microfluidic differential manometer for cellular-scale hydrodynamics. Proc. Natl Acad. Sci. USA 103, 538–542.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bertram, C. D. & Tscherry, J. 2006 The onset offlow-rate limitation and flow-induced oscillations in collapsible tubes. J. Fluids Struct. 22, 1029–1045.Google Scholar
Bruss, H. 2008 Theoretical Microfluidics. Oxford University Press.Google Scholar
Bruun, H. H. 1995 Hot-wire Anemometry: Principles and Signal Analysis. Oxford University Press.CrossRefGoogle Scholar
Carpenter, P. W. & Pedley, T. J. (Eds) 2003 IUTAM Symposium on Flow Past Highly Compliant Boundaries and in Collapsible Tubes. Kluwer.CrossRefGoogle Scholar
Deck, L. & de Groot, P. 1994 High-speed noncontact profiler based on scanning white light interferometry. Appl. Opt. 33, 7334–7338.Google Scholar
Ekinci, K. L., Karabacak, D. M. & Yakhot, V. 2008 Universality in oscillating flows. Phys. Rev. Lett. 101, 264501.Google Scholar
Gervais, T., El-Ali, J., Günther, A. & Jensen, F. K. 2006 Flow-induced deformation of shallow microfluidic channels. Lab on a Chip 6, 500–507.Google Scholar
Grotberg, J. B. & Jensen, O. E. 2004 Biofluid mechanics in flexible tubes. Annu. Rev. Fluid Mech. 36, 121–147.Google Scholar
Hardy, B. S., Uechi, K., Zhen, J. & Kavehpour, H. P. 2009 The deformation of flexible PDMS microchannels under a pressure driven flow. Lab on a Chip 9, 935–938.Google Scholar
Heil, M. 1997 Stokes flow in collapsible tubes: computation and experiment. J. Fluid Mech. 353, 285–312.Google Scholar
Heil, M. & Jensen, O. 2003 Flows in deformable tubes and channels – theoretical models and biological applications. In IUTAM Symposium on Flow Past Highly Compliant Boundaries and in Collapsible Tubes (ed. Carpenter, P. W. & Pedley, T. J.), chap. 2, pp. 15–50. Kluwer.CrossRefGoogle Scholar
Holmes, D. P., Tavakol, B., Froehlicher, G. & Stone, H. A. 2013 Control and manipulation of microfluidic flow via elastic deformations. Soft Matter 9, 7049–7053.Google Scholar
Hosoi, A. E. & Mahadevan, L. 2004 Peeling, heeling, and bursting in a lubricated elastic sheet. Phys. Rev. Lett. 93, 137802.Google Scholar
Huang, L. 2001 Viscous flutter of a finite elastic membrane in Poiseuille flow. J. Fluids Struct. 15, 1061–1088.Google Scholar
Kohl, M. C., Abdel-Khalik, S. I., Jeter, S. M. & Sadowski, D. L. 2005 A microfluidic experimental platform with internal pressure measurements. Sensors Actuators A Phys. 118, 212–221.Google Scholar
Ku, D. N. 1997 Blood flow in arteries. Annu. Rev. Fluid Mech. 29, 399–434.CrossRefGoogle Scholar
Lasheras, J. C. 2007 The biomechanics of arterial aneurysms. Annu. Rev. Fluid Mech. 39, 293–319.Google Scholar
Lissandrello, C., Yakhot, V. & Ekinci, K. L. 2012 Crossover from hydrodynamics to the kinetic regime in confined nanoflows. Phys. Rev. Lett. 108, 084501.Google Scholar
McKeon, B. J. 2007 Velocity, vorticity, and Mach number. In Springer Handbook of Experimental Fluid Mechanics (ed. Yarin, A., Tropea, C. & Foss, J. F.), chap. 5, pp. 215–471. Springer.Google Scholar
Orth, A., Schonbrun, E. & Crozier, K. B. 2011 Multiplexed pressure sensing with elastomer membranes. Lab on a Chip 11, 3810–3815.Google Scholar
Pedley, T. & Lou, X. Y. 1998 Modelling flow and oscillations in collapsible tubes. Theor. Comput. Fluid Dyn. 10, 277–294.Google Scholar
Popel, A. S. & Johnson, P. C. 2005 Microcirculation and hemorheology. Annu. Rev. Fluid Mech. 37, 43–69.Google Scholar
Sampathkumar, A., Ekinci, K. L. & Murray, T. W. 2011 Multiplexed optical operation of distributed nanoelectromechanical systems arrays. Nano Lett. 11, 1014–1019.Google Scholar
Schoch, R. B., Han, J. & Renaud, P. 2008 Transport phenomena in nanofluidics. Rev. Mod. Phys. 80, 839–883.CrossRefGoogle Scholar
Shelley, M., Vanderberghe, N. & Zhang, J. 2005 Heavy flags undergo spontaneous oscillations in flowing water. Phys. Rev. Lett. 94, 094302.Google Scholar
Small, M. K. & Nix, W. D. 1992 Analysis of the accuracy of the bulge test in determining the mechanical properties of thin films. J. Mater. Res. 7, 1553–1563.CrossRefGoogle Scholar
Song, W. & Psaltis, D. 2011 Optofluidic membrane interferometer: a imaging method for measuring microfluidic pressure and flow rate simultaneously on a chip. Biomicrofluidics 5, 044110.Google Scholar
Srivastava, N. & Burns, M. A. 2007 Microfluidic pressure sensing using trapped air compression. Lab on a Chip 7, 633–637.Google Scholar
Stone, H. A., Stroock, A. D. & Ajdari, A. 2004 Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 36, 381–411.Google Scholar
Sutera, S. P. & Skalak, R. 1993 The history of Poiseuille’s law. Annu. Rev. Fluid Mech. 25, 1–20.Google Scholar
Whitesides, G. M. & Stroock, A. D. 2001 Flexible methods for microfluidics. Phys. Today 54, 42–48.Google Scholar
Whittaker, R. J., Heil, M., Jensen, O. E. & Waters, S. L. 2010 A rational derivation of a tube law from shell theory. Q. J. Mech. Appl. Maths 63, 465–496.Google Scholar