Article contents
Non-Gaussianity in turbulent relative dispersion
Published online by Cambridge University Press: 29 March 2019
Abstract
We present an extension of Thomson’s (J. Fluid Mech., vol. 210, 1990, pp. 113–153) two-particle Lagrangian stochastic model that is constructed to be consistent with the 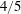 $4/5$ law of turbulence. The rate of separation in the new model is reduced relative to the original model with zero skewness in the Eulerian longitudinal relative velocity distribution and is close to recent measurements from direct numerical simulations of homogeneous isotropic turbulence. The rate of separation in the equivalent backwards dispersion model is approximately a factor of 2.9 larger than the forwards dispersion model, a result that is consistent with previous work.
$4/5$ law of turbulence. The rate of separation in the new model is reduced relative to the original model with zero skewness in the Eulerian longitudinal relative velocity distribution and is close to recent measurements from direct numerical simulations of homogeneous isotropic turbulence. The rate of separation in the equivalent backwards dispersion model is approximately a factor of 2.9 larger than the forwards dispersion model, a result that is consistent with previous work.
- Type
- JFM Papers
- Information
- Copyright
- © Crown Copyright. Published by Cambridge University Press 2019
References
- 1
- Cited by


