Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T22:34:19.719Z Has data issue: false hasContentIssue false
  • English
  • Français

The non-equilibrium region of grid-generated decaying turbulence

Published online by Cambridge University Press:  13 March 2014

P. C. Valente  and
J. C. Vassilicos
P. C. Valente*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
J. C. Vassilicos
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Present address: IDMEC/IST, University of Lisbon, 1049-001 Lisbon, Portugal. Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The previously reported non-equilibrium dissipation law is investigated in turbulent flows generated by various regular and fractal square grids. The flows are documented in terms of various turbulent profiles which reveal their differences. In spite of significant inhomogeneity and anisotropy differences, the new non-equilibrium dissipation law is observed in all of these flows. 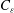Various transverse and longitudinal integral scales are measured and used to define the dissipation coefficient $C_{\varepsilon }$. It is found that the new non-equilibrium dissipation law is not an artefact of a particular choice of the integral scale and that the usual equilibrium dissipation law can actually coexist with the non-equilibrium law in different regions of the same flow.

JFM classification

Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 744 , 10 April 2014 , pp. 5 - 37
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. 2003 On estimating mean and instantaneous turbulent energy dissipation rates with hot wires. Exp. Therm. Fluid Sci. 27, 151–157.CrossRefGoogle Scholar
Antonia, R. A., Browne, L. W. B. & Chambers, A. J. 1984 On the spectrum of the transverse derivative of the streamwise velocity in a turbulent flow. Phys. Fluids 27 (11).CrossRefGoogle Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Benedict, L. H. & Gould, R. D. 1996 Towards better uncertainty estimates for turbulent statistics. Exp. Fluids 22, 129–136.CrossRefGoogle Scholar
Browne, L. W. B., Antonia, R. A. & Shah, D. A. 1987 Turbulent energy dissipation in a wake. J. Fluid Mech. 179, 307–326.CrossRefGoogle Scholar
Burattini, P. 2008 The effect of the X-wire probe resolution in measurements of isotropic turbulence. Meas. Sci. Technol. 19, 115405.CrossRefGoogle Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2005 On the normalized turbulent energy dissipation rate. Phys. Fluids 17, 098103.CrossRefGoogle Scholar
Corrsin, S. 1963 Handbook der Physik. vol. 8, pp. 524–590. Springer.Google Scholar
Discetti, S., Ziskin, I. B., Astarita, T., Adrian, R. J. & Prestridge, K. P. 2013 PIV measurements of anisotropy and inhomogeneity in decaying fractal generated turbulence. Fluid Dyn. Res. 45, 061401.Google Scholar
Ertunç, Ö., Özyilmaz, N., Lienhart, H., Durst, F. & Beronov, K. 2010 Homogeneity of turbulence generated by static-grid structures. J. Fluid Mech. 654 (1), 473–500.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of AN Kolmogorov. Cambridge University Press.Google Scholar
George, W. K. & Hussein, H. J. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.CrossRefGoogle Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2012 Particle image velocimetry study of fractal-generated turbulence. J. Fluid Mech. 711, 306–336.Google Scholar
Hunt, J. C. R. & Graham, J. M. R. 1978 Free-stream turbulence near plane boundaries. J. Fluid Mech. 84 (2), 209–235.Google Scholar
Hurst, D. J. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19, 035103.CrossRefGoogle Scholar
Jackson, R., Graham, J. M. R. & Maull, D. J. 1973 The lift on a wing in a turbulent flow. Aeronaut. Q. 24, 155–166.CrossRefGoogle Scholar
Jayesh,  & Warhaft, Z. 1992 Probability distribution, conditional dissipation, and transport of passive temperature fluctuations in grid-generated turbulence. Phys. Fluids 4, 2292–2307.Google Scholar
Krogstad, P.-Å. & Davidson, P. A. 2012 Near-field investigation of turbulence produced by multi-scale grids. Phys. Fluids 24, 035103.CrossRefGoogle Scholar
Laizet, S. & Vassilicos, J. C. 2011 DNS of fractal-generated turbulence. Flow Turbul. Combust. 87, 673–705.Google Scholar
Lumley, J. L. 1992 Some comments on turbulence. Phys. Fluids 4 (2), 203–211.Google Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22, 075101.CrossRefGoogle Scholar
Mestayer, P. & Chambaud, P. 1979 Some limitations to measurements of turbulence micro-structure with hot and cold wires. Boundary-Layer Meteorol. 16, 311–329.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics. vol. vol. 2. MIT Press.Google Scholar
Nagata, K., Sakai, Y., Inaba, T., Suzuki, H., Terashima, O. & Suzuki, H. 2013 Turbulence structure and turbulence kinetic energy transport in multiscale/fractal-generated turbulence. Phys. Fluids 25 (065102).CrossRefGoogle Scholar
Oxlade, A. R., Valente, P. C., Ganapathisubramani, B. & Morrison, J. F. 2012 Denoising of time-resolved PIV for accurate measurement of turbulence spectra and reduced error in derivatives. Exp. Fluids 53 (5), 1561–1575.Google Scholar
Pearson, B. R., Krogstad, P. Å & van de Water, W. 2002 Measurements of the turbulent energy dissipation rate. Phys. Fluids 14, 1288–1290.Google Scholar
Perry, A. E. 1982 Hot-wire Anemometry. Clarendon Press.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
Seoud, R. E. & Vassilicos, J. C. 2007 Dissipation and decay of fractal-generated turbulence. Phys. Fluids 19, 105108.Google Scholar
Sreenivasan, K. R. 1984 On the scaling of the turbulence energy dissipation rate. Phys. Fluids 27, 1048–1051.Google Scholar
Sreenivasan, K. R. 1995 The energy dissipation rate in turbulent shear flows. In Developments in Fluid Dynamics and Aerospace Engineering (ed. Deshpande, S. M., Prabhu, A., Sreenivasan, K. R. & Viswanath, P. R.), pp. 159–190. Interline Publishers.Google Scholar
Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10, 528–529.Google Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. A 151 (873), 421–444.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. 2nd edn. MIT Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tsinober, A., Kit, E. & Dracos, T. 1992 Experimental investigation of the field of velocity gradients in turbulent flows. J. Fluid Mech. 242, 169–192.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2011 The decay of turbulence generated by a class of multi-scale grids. J. Fluid Mech. 687, 300–340.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Universal dissipation scaling for nonequilibrium turbulence. Phys. Rev. Lett. 108, 214503.CrossRefGoogle ScholarPubMed
Zhu, Y. & Antonia, R. A. 1995 The spatial resolution of two X-probes for velocity derivative measurements. Meas. Sci. Technol. 6, 538–549.CrossRefGoogle Scholar
Zhu, Y. & Antonia, R. A. 1996 The spatial resolution of hot-wire arrays for the measurement of small-scale turbulence. Meas. Sci. Technol. 7, 1349–1359.Google Scholar
Zhu, Y., Antonia, R. A. & Chua, L. P. 2002 Performance of a probe for measuring turbulent energy and temperature dissipation rates. Exp. Fluids 33, 334–345.Google Scholar