Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T03:55:29.565Z Has data issue: false hasContentIssue false
  • English
  • Français

New correlation formulae for the straight section of the electrospun jet from a polymer drop

Published online by Cambridge University Press:  23 October 2013

R. Sahay ,
C. J. Teo  and
Y. T. Chew
R. Sahay
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 9 Engineering Drive 1, Singapore 117576, Singapore
C. J. Teo*
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 9 Engineering Drive 1, Singapore 117576, Singapore
Y. T. Chew
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 9 Engineering Drive 1, Singapore 117576, Singapore
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An electrospun polymer jet issued from a Taylor cone follows a straight-line motion before experiencing electrical bending instability resulting in curling and spiralling of the jet in three-dimensional space. Experiments are performed to characterize the fluid dynamics of an electrospun polymer jet. Appropriate image processing is performed to systematically analyse flow regimes of the electrospun jet. These regimes include Taylor cone formation/jet initiation and the straight section of the jet. Dimensional analysis was performed to identify the salient dimensionless parameters, which govern the electrospun jet characteristics. 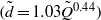Three new correlation formulae were obtained to characterize the dimensionless jet diameter at the apex of the Taylor cone $(\tilde {d} = 1. 03{\tilde {Q} }^{0. 44} )$, the dimensionless jet diameter at different locations along the jet’s straight section 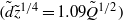$(\tilde {d} {\tilde {z} }^{1/ 4} = 1. 09{\tilde {Q} }^{1/ 2} )$, as well as the length of the straight section of the jet 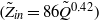$({\tilde {Z} }_{in} = 86{\tilde {Q} }^{0. 42} )$. These correlation formulae are valid for the analysed range of dimensionless flow rates 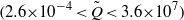$(2. 6{{\times 10}}^{- 4} \lt \tilde {Q} \lt 3. 6{{\times 10}}^{7} )$ and dimensionless electric fields 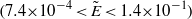$(7. 4{{\times 10}}^{- 4} \lt \tilde {E} \lt 1. 4{{\times 10}}^{- 1} )$. In addition, the correlation formulae are valid for the analysed range of Deborah numbers De and Reynolds numbers Re based on nozzle radius, 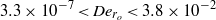$3. 3\times {10}^{- 7} \lt {\mathit{De}}_{{r}_{o} } \lt 3. 8\times {10}^{- 2} $ and 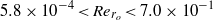$5. 8\times {10}^{- 4} \lt {\mathit{Re}}_{{r}_{o} } \lt 7. 0\times {10}^{- 1} $. The proposed new correlation formulae are instrumental in the design as well as controlled manipulation/optimization of the electrospinning phenomenon.

JFM classification

Wakes/Jets: Jets Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Materials Processing Flows: Polymer processing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 735 , 25 November 2013 , pp. 150 - 175
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afifi, A. M., Yamane, H. & Kimura, Y. 2010 Effect of polymer molecular weight on the electrospinning of polylactides in entangled and aligned fibre forms. Sen-I Gakkaishi 66, 35–42.CrossRefGoogle Scholar
Ansari, A. A., Sumana, G., Khan, R. & Malhotra, B. D. 2009 Polyaniline–cerium oxide nanocomposite for hydrogen peroxide sensor. J. Nanosci. Nanotechnol. 9, 4679–4685.Google Scholar
Arnolds, O., Buggisch, H., Sachsenheimer, D. & Willenbacher, N. 2010 Capillary breakup extensional rheometry (CaBER) on semi-dilute and concentrated polyethylene oxide (PEO) solutions. Rheol. Acta 49, 1207–1217.Google Scholar
Baik, Y., Lee, S., Jang, Y. & Kim, S. 2005 Unidirectional alignment of Carbon nano-sized fibre using drawing process. J. Mater. Sci. 40, 6037–6039.Google Scholar
Berkland, C., Pack, D. W. & Kim, K. 2004 Controlling surface nano-structure using flow-limited field-injection electrostatic spraying (FFESS) of poly(D,L-lactide-co-glycolide). Biomaterials 25, 5649–5658.Google Scholar
Brandrup, J. & Immergut, E. H. 1966 Polymer Handbook, vol. 1, Interscience.Google Scholar
Cooley, J. F. 1900 Improved methods of and apparatus for electrically separating the relatively volatile liquid component from the component of relatively fixed substances of composite fluids. Patent, GB 06385.Google Scholar
Deitzel, J. M., Kleinmeyer, J., Harris, D. & Beck Tan, N. C. 2001 The effect of processing variables on the morphology of electrospun nanofibres and textiles. Polymer 42, 261–272.Google Scholar
Dougherty, S. & Liang, J. 2009 Fabrication of segmented nanofibres by template wetting of multilayered alternating polymer thin films. J. Nanopart. Res. 11, 743–747.CrossRefGoogle Scholar
Feng, J. J. 2002 The stretching of an electrified non-Newtonian jet, A model for electrospinning. Phys. Fluids 14, 3912–3926.CrossRefGoogle Scholar
Feng, J. J. 2003 Stretching of a straight electrically charged viscoelastic jet. J. Non-Newtonian Fluid Mech. 116, 55–70.Google Scholar
Fong, H., Chun, I. & Reneker, D. H. 1999 Beaded nanofibres formed during electrospinning. Polymer 40, 4585–4592.Google Scholar
Formhals, A. 1938 Artificial fibre construction. Patent, US 2109333.Google Scholar
Formhals, A. 1943 Production of artificial fibres. Patent, US 2323025.Google Scholar
Formhals, A. 1944 Method and apparatus for spinning. Patent, US 2349950.Google Scholar
Greenfeld, I., Fezzaa, K., Rafailovich, M. H. & Zussman, E. 2012 Fast X-ray phase-contrast imaging of electrospinning polymer jets, measurements of radius, velocity, and concentration. Macromolecules 45, 3616–3626.CrossRefGoogle Scholar
Han, T., Yarin, A. L. & Reneker, D. H. 2008 Viscoelastic electrospun jets: initial stresses and elongational rheometry. Polymer 49, 1651–1658.CrossRefGoogle Scholar
Helgeson, M. E., Grammatikos, K. N., Deitzel, J. M. & Wagner, N. J. 2008 Theory and kinematic measurements of the mechanics of stable electrospun polymer jets. Polymer 49, 2924–2936.Google Scholar
Heulings, H. R., Huang, X. Y., Li, J., Yuen, T. & Lin, C. L. 2001 Mn-substituted inorganic–organic hybrid materials based on ZnSe, Nanostructures that may lead to magnetic semiconductors with a strong quantum confinement effect. Nano Lett. 1, 521–525.CrossRefGoogle Scholar
Hipp, W., Karl, H., Grosshans, I. & Stritzker, B. 2003 Quantum confinement in CdSe-nanocrystallites synthesized by ion implantation. Mater. Sci. Eng. B 101, 318–323.Google Scholar
Hohman, M. M. 2000 A physical theory of the instabilities of electrically driven jets. Ph.D. thesis, Department of Physics, University of Chicago.Google Scholar
Hohman, M. M., Shin, M., Rutledge, G. & Brenner, M. P. 2001a Electrospinning and electrically forced jets. I. Stability theory. Phys. Fluids 13, 2201–2220.CrossRefGoogle Scholar
Hohman, M. M., Shin, M., Rutledge, G. & Brenner, M. P. 2001b Electrospinning and electrically forced jets. II. Applications. Phys. Fluids 13, 2221–2236.Google Scholar
Jarusuwannapoom, T., Hongroijanawiwat, W., Jitjaicham, S., Wannatong, L. & Nithitanakul, M. 2005 Effect of solvents on electro-spinnability of polystyrene solutions and morphological appearance of resulting electrospun polystyrene fibres. Eur. Polym. J. 41, 409–421.Google Scholar
Jaworek, A., Krupa, A., Lackowski, M., Sobczyk, A. T. & Czech, T. 2009 Nanocomposite fabric formation by electrospinning and electrospraying technologies. J. Electrostat 67, 435–438.CrossRefGoogle Scholar
Kaplan-Diedrich, H. & Frischat, G. H. 1997 Drawing of oxynitride glass fibres. Glastech. Ber. Glass. Sci. Technol. 70, 109–112.Google Scholar
Kirichenko, V. N., Petryanov Sokolov, I. V., Suprun, N. N. & Shutov, A. A. 1986 Asymptotic radius of a slightly conducting liquid jet in an electric field. Sov. Phys. Dokl 31, 611–613.Google Scholar
Kowalewski, T. A. 1996 On the separation of droplets from a liquid jet. Fluid Dyn. Res. 17, 121–145.Google Scholar
Kowalewski, T. A., Blon Ski, S. & Barral, S. 2005 Experiments and modelling of electrospinning process. Bull. Pol. Ac.: Tech. 53, 385–394.Google Scholar
Mao, H., Lu, X. F., Chao, D. M., Cui, L. L. & Zhang, W. J. 2008 Self-assembly synthesis of hollow, core–shell and solid soluble oligo(3,4-ethylenedioxythiophene)s microspheres in a mixed solvent. Mater. Lett. 62, 2543–2546.Google Scholar
McKee, M. G. 2005 The influence of branching and intermolecular interactions on the formation of electrospun fibres. Ph.D. thesis, Virginia Polytechnic Institute and State University.Google Scholar
Reneker, D. H., Yarin, A. L., Fong, H. & Koombhongse, S. 2000 Bending instability of electrically charged liquid jets of polymer solutions in electrospinning. J. Appl. Phys. 87, 4531–4547.Google Scholar
Reznik, S. & Zussman, E. 2010 Capillary-dominated electrified jets of a viscous leaky dielectric liquid. Phys. Rev. E 81, 026313.Google Scholar
Rutledge, G. C. & Fridrikh, S. V. 2007 Formation of fibres by electrospinning. Adv. Drug Deliv. Rev. 59, 1384–1391.Google Scholar
Salata, O. V. 2005 Tools of nanotechnology, electrospray. Curr. Nanosci. 1, 25–33.Google Scholar
Spivak, A. & Dzenis, Y. 1998 Asymptotic decay of radius of a weakly conductive viscous jet in an external electric field. Appl. Phys. Lett. 73, 3067–3069.Google Scholar
Suen, S. C., Whang, W. T., Hou, F. J. & Dai, B. T. 2006 Low-temperature self-assembly of copper phthalocyanine nanofibres. Org. Electron. 7, 428–434.Google Scholar
Tan, S. H., Inai, R., Kotaki, M. & Ramakrishna, S. 2005 Systematic parameter study for ultra-fine fibre fabrication via electrospinning process. Polymer 46, 6128–6134.Google Scholar
Tang, J., Brzozowski, L., Barkhouse, D. A. R., Wang, X. H. & Debnath, R. 2010 Quantum dot photovoltaics in the extreme quantum confinement regime, the surface-chemical origins of exceptional air- and light-stability. ACS Nano 4, 869–878.Google Scholar
Taylor, G. I. 1964 Disintegration of water drops in an electric field. Proc. R. Soc. Lond. Ser. A 280, 383–397.Google Scholar
Taylor, G. I. 1969 Electrically driven jets. Proc. R. Soc. London 313, 453–475.Google Scholar
Theron, S. A., Zussman, E. & Yarin, A. L. 2004 Experimental investigation of the governing parameters in the electrospinning of polymer solutions. Polymer 45, 2017–2030.Google Scholar
Thompson, C. J., Chase, G. G., Yarin, A. L. & Reneker, D. H. 2007 Effects of parameters on nanofibre diameter determined from electrospinning model. Polymer 48, 6913–6922.Google Scholar
Vohra, V., Giovanella, U., Tubino, R., Murata, H. & Botta, C. 2011 Electroluminescence from conjugated polymer electrospun nanofibres in solution processable organic light-emitting diodes. ACS Nano 5, 5572–5578.CrossRefGoogle Scholar
Wang, C., Cheng, Y. W., Hsu, C. H., Chien, H. S. & Tsou, S. Y. 2011 How to manipulate the electrospinning jet with controlled properties to obtain uniform fibres with the smallest diameter? A brief discussion of solution electrospinning process. J. Polym. Res. 18, 111–123.Google Scholar
Wu, Y. & Clark, R. L. 2008 Electrohydrodynamic atomization, a versatile process for preparing materials for biomedical applications. J. Biomater. Sci., Polym. Ed. 19, 573–601.CrossRefGoogle ScholarPubMed
Yarin, A. L. 1993 Free Liquid Jets and Films: Hydrodynamics and Rheology. Longman Scientific & Technical and John Wiley & Sons.Google Scholar
Yarin, A. L., Kataphinan, W. & Reneker, D. H. 2005 Branching in electrospinning of nanofibres. J. Appl. Phys. 98, 1–12.Google Scholar
Yarin, A. L., Koombhongse, S. & Reneker, D. H. 2001a Bending instability in electrospinning of nanofibres. J. Appl. Phys. 89, 3018–3026.Google Scholar
Yarin, A. L., Koombhongse, S. & Reneker, D. H. 2001b Taylor cone and jetting from liquid droplets in electrospinning of nanofibres. J. Appl. Phys. 90, 4836–4846.Google Scholar
Yoffe, A. D. 1993 Low-dimensional systems – quantum-size effects and electronic-properties of semiconductor microcrystallites (zero-dimensional systems) and some quasi-two-dimensional systems. Adv. Phys. 42, 173–266.Google Scholar
Zeleny, J. 1914 The electrical discharge from liquid points, and a hydrostatic method of measuring the electric intensity at their surfaces. Phys. Rev. 3, 69–91.Google Scholar
Zeleny, J. 1917 Instability of electrified liquid surfaces. Phys. Rev. 10, 1–6.Google Scholar
Zhang, L. F & Hsieh, Y. L. 2008 Ultra-fine cellulose acetate/poly(ethylene oxide) bicomponent fibres. Carbohydr. Polym. 71, 196–207.Google Scholar
Zhang, L & Liu, P. 2008 Facile fabrication of uniform polyaniline nanotubes with tubular aluminosilicates as templates. Nanoscale Res. Lett. 3, 299–302.CrossRefGoogle Scholar
Zhang, P., Shao, C., Zhang, Z., Zhang, M. & Mu, J. 2011 TiO2@carbon core/shell nanofibres, controllable preparation and enhanced visible photocatalytic properties. Nanoscale 3, 2943–2949.Google Scholar
Zuo, W., Zhu, M., Yang, W., Yu, H., Chen, Y. & Zhang, Y. 2005 Experimental study on relationship between jet instability and formation of beaded fibres during electrospinning. Polym. Engng Sci. 45, 704–709.CrossRefGoogle Scholar