Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-05T15:40:45.273Z Has data issue: false hasContentIssue false
  • English
  • Français

The multi-scale geometry of the near field in an axisymmetric jet

Published online by Cambridge University Press:  18 January 2018

Dhiren Mistry Open the ORCID record for Dhiren Mistry [Opens in a new window] ,
James R. Dawson  and
Alan R. Kerstein
Dhiren Mistry*
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
James R. Dawson
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
Alan R. Kerstein
Affiliation:
72 Lomitas Road, Danville, CA 94526, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A characteristic feature of axisymmetric jets, and turbulent shear flows in general, is the entrainment of mass across the turbulent/non-turbulent interface (TNTI). The multi-scale nature of the TNTI surface area was recently observed to exhibit power-law scaling with a fractal dimension, 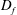$D_{f}$, between 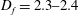$D_{f}=2.3{-}2.4$, inferred from two-dimensional data, in both high Reynolds number boundary layers and the far field of axisymmetric jets. In this paper, we show that the fractal scaling previously observed in the far field of an axisymmetric jet is established at the end of the potential core. Simultaneous measurements of the velocity and scalar fields were obtained and coarse grain filtering was applied over two decades of scale separation, showing that 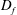$D_{f}$ evolves to 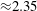${\approx}2.35$ at 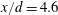$x/d=4.6$, which is similar to 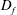$D_{f}$ found in the far field between 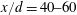$x/d=40{-}60$. This is evidence that scale separation becomes sufficiently developed to achieve scale invariance of the TNTI surface area in the near field of the jet well before self-similarity is established. We also observe that the onset of this geometric scale invariance coincides with the onset of radial homogeneity shown by two-point velocity correlations. Finally, we present a simple theoretical basis for these results using an exact fractal construction based on the Koch curve and applying a coarse-grain filtering analysis.

JFM classification

Nonlinear Dynamical Systems: Fractals Turbulent Flows: Turbulent Flows Wakes/Jets: Wakes/Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 838 , 10 March 2018 , pp. 501 - 515
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Borrell, G. & Jiménez, J. 2016 Properties of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 801, 554–596.CrossRefGoogle Scholar
Charlette, F., Meneveau, C. & Veynante, D. 2002 A power-law flame wrinkling model for LES of premixed turbulent combustion Part I. non-dynamic formulation and initial tests. Combust. Flame 131 (1–2), 159–180.Google Scholar
Chatakonda, O., Hawkes, E. R., Aspden, A. J., Kerstein, A. R., Kolla, H. & Chen, J. H. 2013 On the fractal characteristics of low Damkholer number flames. Combust. Flame 160 (11), 2422–2433.Google Scholar
Chauhan, K., Philip, J., de Silva, C., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.Google Scholar
Corrsin, S. & Kistler, A.1955 Free-stream boundaries of turbulent flows. Tech. Rep. TN-1244. NASA, Baltimore.Google Scholar
Crimaldi, J. P. 2008 Planar laser induced fluorescence in aqueous flows. Exp. Fluids 44, 851–863.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Fellouah, H. & Pollard, A. 2009 The velocity spectra and turbulence length scale distributions in the near to intermediate regions of a round free turbulent jet. Phys. Fluids 21, 115101.CrossRefGoogle Scholar
Hawkes, E. R., Chatakonda, O., Kolla, H., Kerstein, A. R. & Chen, J. H. 2012 A petascale direct numerical simulation study of the modelling of flame wrinkling for large-eddy simulations in intense turbulence. Combust. Flame 159 (8), 2690–2707.CrossRefGoogle Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2015 The turbulent/non-turbulent interface in an inclined dense gravity current. J. Fluid Mech. 765, 303–324.CrossRefGoogle Scholar
Mandelbrot, B. B. 1982 The Fractal Geometry of Nature. W. H. Freeman and Company.Google Scholar
Mathew, J. & Basu, A. 2002 Some characteristics of entrainment at a cylindrical turbulence boundary. Phys. Fluids 14 (7), 2065–2072.Google Scholar
Mistry, D., Philip, J., Dawson, J. R. & Marusic, I. 2016 Entrainment at multi-scales across the turbulent/non-turbulent interface in an axisymmetric jet. J. Fluid Mech. 802, 690–725.Google Scholar
Prasad, R. R. & Sreenivasan, K. R. 1989 Scalar interfaces in digital images of turbulent flows. Exp. Fluids 7, 259–264.Google Scholar
van Reeuwijk, M. & Holzner, M. 2014 The turbulence boundary of a temporal jet. J. Fluid Mech. 739, 254–275.Google Scholar
da Silva, C., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46 (1), 567–590.CrossRefGoogle Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent-nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111, 044501.Google Scholar
Sreenivasan, K. R. & Meneveau, C. 1986 The fractal facets of turbulence. J. Fluid Mech. 173, 357–386.Google Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421, 79–108.Google Scholar
Taveira, R. R. & da Silva, C. B. 2014 Characteristics of the viscous superlayer in shear free turbulence and in planar turbulent jets. Phys. Fluids 26, 021702.Google Scholar
Trouvé, A. & Poinsot, T. 1994 The evolution equation for the flame surface density in turbulent premixed combustion. J. Fluid Mech. 278, 1–31.CrossRefGoogle Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2015 Turbulent mixing of passive scalar near turbulent and non-turbulent interface in mixing layers. Phys. Fluids 27, 085109.CrossRefGoogle Scholar
Westerweel, J., Fukushima, C., Pedersen, J. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.Google Scholar
Westerweel, J., Hofmann, T., Fukushima, C. & Hunt, J. C. R. 2002 The turbulent/non-turbulent interface at the outer boundary of a self-similar turbulent jet. Exp. Fluids 33, 873–878.Google Scholar