Published online by Cambridge University Press: 23 April 2019
We report on experiments of turbulent particle-laden plumes descending through a stratified environment. We show that provided the characteristic plume speed 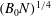 $(B_{0}N)^{1/4}$ exceeds the particle fall speed, where the plume buoyancy flux is
$(B_{0}N)^{1/4}$ exceeds the particle fall speed, where the plume buoyancy flux is 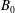 $B_{0}$ and the Brunt–Väisälä frequency is
$B_{0}$ and the Brunt–Väisälä frequency is 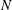 $N$, then the plume is arrested by the stratification and initially intrudes at the neutral height associated with a single-phase plume of the same buoyancy flux. If the original fluid phase in the plume has density equal to that of the ambient fluid at the source, then as the particles sediment from the intruding fluid, the fluid finds itself buoyant and rises, ultimately intruding at a height of about
$N$, then the plume is arrested by the stratification and initially intrudes at the neutral height associated with a single-phase plume of the same buoyancy flux. If the original fluid phase in the plume has density equal to that of the ambient fluid at the source, then as the particles sediment from the intruding fluid, the fluid finds itself buoyant and rises, ultimately intruding at a height of about  $0.58\pm 0.03$ of the original plume height, consistent with new predictions we present based on classical plume theory. We generalise this result, and show that if the buoyancy flux at the source is composed of a fraction
$0.58\pm 0.03$ of the original plume height, consistent with new predictions we present based on classical plume theory. We generalise this result, and show that if the buoyancy flux at the source is composed of a fraction 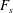 $F_{s}$ associated with the buoyancy of the source fluid, and a fraction
$F_{s}$ associated with the buoyancy of the source fluid, and a fraction 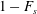 $1-F_{s}$ from the particles, then following the sedimentation of the particles, the plume fluid intrudes at a height
$1-F_{s}$ from the particles, then following the sedimentation of the particles, the plume fluid intrudes at a height 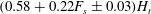 $(0.58+0.22F_{s}\pm 0.03)H_{t}$, where
$(0.58+0.22F_{s}\pm 0.03)H_{t}$, where 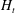 $H_{t}$ is the maximum plume height. This is key for predictions of the environmental impact of any material dissolved in the plume water which may originate from the particle load. We also show that the particles sediment at their fall speed through the fluid below the maximum depth of the plume as a cylindrical column whose area scales as the ratio of the particle flux at the source to the fall speed and concentration of particles in the plume at the maximum depth of the plume before it is arrested by the stratification. We demonstrate that there is negligible vertical transport of fluid in this cylindrical column, but a series of layers of high and low particle concentration develop in the column with a vertical spacing which is given by the ratio of the buoyancy of the particle load and the background buoyancy gradient. Small fluid intrusions develop at the side of the column associated with these layers, as dense parcels of particle-laden fluid convect downwards and then outward once the particles have sedimented from the fluid, with a lateral return flow drawing in ambient fluid. As a result, the pattern of particle-rich and particle-poor layers in the column gradually migrates upwards owing to the convective transport of particles between the particle-rich layers superposed on the background sedimentation. We consider the implications of the results for mixing by bubble plumes, for submarine blowouts of oil and gas and for the fate of plumes of waste particles discharged at the ocean surface during deep-sea mining.
$H_{t}$ is the maximum plume height. This is key for predictions of the environmental impact of any material dissolved in the plume water which may originate from the particle load. We also show that the particles sediment at their fall speed through the fluid below the maximum depth of the plume as a cylindrical column whose area scales as the ratio of the particle flux at the source to the fall speed and concentration of particles in the plume at the maximum depth of the plume before it is arrested by the stratification. We demonstrate that there is negligible vertical transport of fluid in this cylindrical column, but a series of layers of high and low particle concentration develop in the column with a vertical spacing which is given by the ratio of the buoyancy of the particle load and the background buoyancy gradient. Small fluid intrusions develop at the side of the column associated with these layers, as dense parcels of particle-laden fluid convect downwards and then outward once the particles have sedimented from the fluid, with a lateral return flow drawing in ambient fluid. As a result, the pattern of particle-rich and particle-poor layers in the column gradually migrates upwards owing to the convective transport of particles between the particle-rich layers superposed on the background sedimentation. We consider the implications of the results for mixing by bubble plumes, for submarine blowouts of oil and gas and for the fate of plumes of waste particles discharged at the ocean surface during deep-sea mining.