Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gavrilyuk, I.
Hermann, M.
Trotsenko, Yu.
and
Timokha, A.
2013.
Studying the coupled eigenoscillations of an axisymmetric tower-elevated tank system by the multimodal method.
Journal of Fluids and Structures,
Vol. 42,
Issue. ,
p.
152.
Gavrilyuk, I P
Hermann, M
Lukovsky, I A
Solodun, O V
and
Timokha, A N
2013.
Weakly nonlinear sloshing in a truncated circular conical tank.
Fluid Dynamics Research,
Vol. 45,
Issue. 5,
p.
055512.
Buldakov, Eugeny
2014.
Lagrangian modelling of fluid sloshing in moving tanks.
Journal of Fluids and Structures,
Vol. 45,
Issue. ,
p.
1.
2015.
Ships and Offshore Structures XIX.
p.
73.
Temarel, P.
Bai, W.
Bruns, A.
Derbanne, Q.
Dessi, D.
Dhavalikar, S.
Fonseca, N.
Fukasawa, T.
Gu, X.
Nestegård, A.
Papanikolaou, A.
Parunov, J.
Song, K.H.
and
Wang, S.
2016.
Prediction of wave-induced loads on ships: Progress and challenges.
Ocean Engineering,
Vol. 119,
Issue. ,
p.
274.
Hara, Kensuke
and
Watanabe, Masahiro
2016.
Formulation of the nonlinear sloshing-structure coupled problem based on the Hamiltonian mechanics for constraint systems.
Journal of Fluids and Structures,
Vol. 62,
Issue. ,
p.
104.
Faltinsen, Odd M.
Lukovsky, Ivan A.
and
Timokha, Alexander N.
2016.
Resonant sloshing in an upright annular tank.
Journal of Fluid Mechanics,
Vol. 804,
Issue. ,
p.
608.
Wang, Li-Shi
Wang, Zhuang
and
Li, Yu-Chun
2017.
Two-dimensional nonlinear parametric sloshing in the irregular tanks: numerical analysis and experimental investigation.
Journal of Vibroengineering,
Vol. 19,
Issue. 3,
p.
2153.
Lukovsky, I. A.
and
Timokha, A. N.
2017.
Multimodal Method in Sloshing.
Journal of Mathematical Sciences,
Vol. 220,
Issue. 3,
p.
239.
Dalmon, A.
Lepilliez, M.
Tanguy, S.
Pedrono, A.
Busset, B.
Bavestrello, H.
and
Mignot, J.
2018.
Direct numerical simulation of a bubble motion in a spherical tank under external forces and microgravity conditions.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
467.
Zhao, W.
Taylor, P. H.
Wolgamot, H. A.
and
Eatock Taylor, R.
2018.
Identifying linear and nonlinear coupling between fluid sloshing in tanks, roll of a barge and external free-surface waves.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
403.
Wang, Jiadong
Lo, Sai Huen
Zhou, Ding
Dong, Yun
and
Pellicano, Francesco
2019.
Nonlinear Sloshing of Liquid in a Rigid Cylindrical Container with a Rigid Annular Baffle under Lateral Excitation.
Shock and Vibration,
Vol. 2019,
Issue. 1,
Yu, Yang
Zhao, Tianfeng
Duan, Menglan
Zhou, Tongming
Xu, Jing
Su, Yangxuan
Zhong, Zicheng
and
Liu, Houfa
2019.
Experimental investigation on the underwater soft yoke mooring system considering sloshing.
Ships and Offshore Structures,
Vol. 14,
Issue. 3,
p.
309.
Hara, Kensuke
and
Watanabe, Masahiro
2020.
Application of the DAE approach to the nonlinear sloshing problem.
Nonlinear Dynamics,
Vol. 99,
Issue. 3,
p.
2065.
Solodun, A. V.
and
Timokha, A. N.
2020.
Applied Mathematical Analysis: Theory, Methods, and Applications.
Vol. 177,
Issue. ,
p.
267.
Sabaghzadeh, Hossein
and
Shafaee, Mazyar
2021.
Reversal modeling and optimal design of hyper-elastic diaphragm in space fuel tanks.
SN Applied Sciences,
Vol. 3,
Issue. 10,
KORKMAZ, Fatih Cüneyd
YİGİT, Kenan
and
GÜZEL, Bülent
2021.
Perde Tipi Engellerin Çalkantı Yüklerini Azaltma Etkileri Üzerine Deneysel Bir Çalışma.
El-Cezeri Fen ve Mühendislik Dergisi,
Zhang, Zili
2022.
Understanding and exploiting the nonlinear behavior of tuned liquid dampers (TLDs) for structural vibration control by means of a nonlinear reduced-order model (ROM).
Engineering Structures,
Vol. 251,
Issue. ,
p.
113524.
Meng, Xun
Sun, Ying
Wang, Jiadong
Huo, Ruili
and
Zhou, Ding
2023.
Nonlinear semi-analytical modeling of liquid sloshing in rectangular container with horizontal baffles.
Applied Mathematics and Mechanics,
Vol. 44,
Issue. 11,
p.
1973.
Wu, Chih-Hua
Hung, Tin-Kan
and
Chen, Bang-Fuh
2023.
Kinematic, dynamic and energy characteristics of swirling sloshing waves.
Ocean Engineering,
Vol. 272,
Issue. ,
p.
113875.
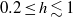 $0. 2\leq h\lesssim 1$. Discrepancy for higher liquid depths
$0. 2\leq h\lesssim 1$. Discrepancy for higher liquid depths 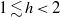 $1\lesssim h\lt 2$ are explained by secondary resonance.
$1\lesssim h\lt 2$ are explained by secondary resonance.