Published online by Cambridge University Press: 18 October 2022
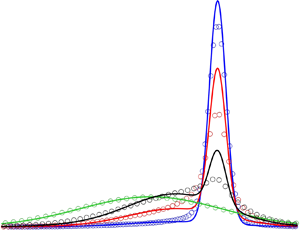
The classical Mott-Smith solution for one-dimensional normal shock wave structure is extended to the two-dimensional regular shock reflection problem. The solution for the non-equilibrium molecular velocity distribution function along the symmetry-plane streamline is obtained as a weighted sum of four Maxwellians. An analysis of applicability of the solution has been performed using the results of direct simulation Monte Carlo calculations for a range of incident shock wave intensities. Accuracy of the solution improves with increasing  $Ma_n$, the Mach number normal to the shock front, so that the solution becomes rather accurate for strong shocks with
$Ma_n$, the Mach number normal to the shock front, so that the solution becomes rather accurate for strong shocks with  $Ma_n>8$.
$Ma_n>8$.