Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-09T07:43:09.978Z Has data issue: false hasContentIssue false
  • English
  • Français

Momentum transport in Taylor–Couette flow with vanishing curvature

Published online by Cambridge University Press:  04 February 2016

Hannes J. Brauckmann ,
Matthew Salewski  and
Bruno Eckhardt
Hannes J. Brauckmann
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, D-35032 Marburg, Germany
Matthew Salewski
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, D-35032 Marburg, Germany Department of Aerodynamics and Fluid Mechanics, Brandenburg University of Technology Cottbus-Senftenberg, Siemens-Halske-Ring 14, D-03046 Cottbus, Germany
Bruno Eckhardt*
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, D-35032 Marburg, Germany J. M. Burgerscentrum, Delft University of Technology, Mekelweg 2, 2628 CD Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

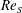We numerically study turbulent Taylor–Couette flow (TCF) between two independently rotating cylinders and the transition to rotating plane Couette flow (RPCF) in the limit of infinite radii. By using the shear Reynolds number $Re_{S}$ and rotation number 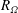$R_{{\it\Omega}}$ as dimensionless parameters, the transition from TCF to RPCF can be studied continuously without singularities. Already for radius ratios 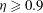${\it\eta}\geqslant 0.9$ we find that the simulation results for various radius ratios and for RPCF collapse as a function of 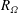$R_{{\it\Omega}}$, indicating a turbulent behaviour common to both systems. We observe this agreement in the torque, mean momentum transport, mean profiles and turbulent fluctuations. Moreover, in TCF and RPCF for 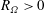$R_{{\it\Omega}}>0$, the profiles in the central region are found to conform with inviscid neutral stability. Intermittent bursts, that have been observed in the outer boundary layer and have been linked to the formation of a torque maximum for counter-rotation, are shown to disappear as 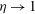${\it\eta}\rightarrow 1$. The corresponding torque maximum disappears as well. Instead, two new maxima of different origin appear for 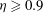${\it\eta}\geqslant 0.9$ and RPCF, a broad and a narrow one, in contrast to the results for smaller 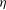${\it\eta}$. The broad maximum at $R_{{\it\Omega}}=0.2$ is connected with a strong vortical flow and can be reproduced by streamwise-invariant simulations. The narrow maximum at 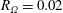$R_{{\it\Omega}}=0.02$ only emerges with increasing 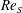$Re_{S}$ and is accompanied by an efficient and correlated momentum transport by the mean flow. Since the narrow maximum is of larger amplitude for 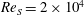$Re_{S}=2\times 10^{4}$, our simulations suggest that it will dominate at even higher 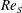$Re_{S}$.

JFM classification

Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 790 , 10 March 2016 , pp. 419 - 452
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. J. A. M. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.CrossRefGoogle ScholarPubMed
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Barri, M. & Andersson, H. I. 2010 Computer experiments on rapidly rotating plane Couette flow. Commun. Comput. Phys. 7 (4), 683–717.Google Scholar
Bech, K. H. & Andersson, H. I. 1997 Turbulent plane Couette flow subject to strong system rotation. J. Fluid Mech. 347, 289–314.Google Scholar
Bilson, M. & Bremhorst, K. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 579, 227–270.CrossRefGoogle Scholar
Bradshaw, P. 1969 The analogy between streamline curvature and buoyancy in turbulent shear flow. J. Fluid Mech. 36, 177–191.Google Scholar
Brauckmann, H. J. & Eckhardt, B. 2013a Direct numerical simulations of local and global torque in Taylor–Couette flow up to $Re=30\,000$ . J. Fluid Mech. 718, 398–427.Google Scholar
Brauckmann, H. J. & Eckhardt, B. 2013b Intermittent boundary layers and torque maxima in Taylor–Couette flow. Phys. Rev. E 87 (3), 033004.Google Scholar
Brethouwer, G., Duguet, Y. & Schlatter, P. 2012 Turbulent-laminar coexistence in wall flows with Coriolis, buoyancy or Lorentz forces. J. Fluid Mech. 704, 137–172.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2007 Temperature gradients, and search for non-Boussinesq effects, in the interior of turbulent Rayleigh–Bénard convection. Europhys. Lett. 80, 14001.Google Scholar
Burin, M. J. & Czarnocki, C. J. 2012 Subcritical transition and spiral turbulence in circular Couette flow. J. Fluid Mech. 709, 106–122.CrossRefGoogle Scholar
Burin, M. J., Schartman, E. & Ji, H. 2010 Local measurements of turbulent angular momentum transport in circular Couette flow. Exp. Fluids 48, 763–769.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability, 1st edn. Clarendon.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21, 385–425.Google Scholar
Coughlin, K. & Marcus, P. S. 1996 Turbulent bursts in Couette–Taylor flow. Phys. Rev. Lett. 77 (11), 2214–2217.CrossRefGoogle ScholarPubMed
Daly, C. A., Schneider, T. M., Schlatter, P. & Peake, N. 2014 Secondary instability and tertiary states in rotating plane Couette flow. J. Fluid Mech. 761, 27–61.Google Scholar
Deguchi, K., Meseguer, A. & Mellibovsky, F. 2014 Subcritical equilibria in Taylor–Couette flow. Phys. Rev. Lett. 112 (18), 184502.Google Scholar
Demay, Y., Iooss, G. & Laure, P. 1992 Wave patterns in the small gap Couette–Taylor problem. Eur. J. Mech. (B/Fluids) 11, 621–634.Google Scholar
Dong, S. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 587, 373–393.CrossRefGoogle Scholar
Dubrulle, B. 1993 Differential rotation as a source of angular momentum transfer in the solar nebula. Icarus 106, 59–76.CrossRefGoogle Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D. & Zahn, J.-P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17 (9), 095103.Google Scholar
Dubrulle, B. & Hersant, F. 2002 Momentum transport and torque scaling in Taylor–Couette flow from an analogy with turbulent convection. Eur. Phys. J. B 26, 379–386.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007a Fluxes and energy dissipation in thermal convection and shear flows. Europhys. Lett. 78, 24001.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007b Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Eckhardt, B. & Yao, D. 1995 Local stability analysis along Lagrangian paths. Chaos, Solitons Fractals 5 (11), 2073–2088.Google Scholar
Esser, A. & Grossmann, S. 1996 Analytic expression for Taylor–Couette stability boundary. Phys. Fluids 8 (7), 1814–1819.Google Scholar
Faisst, H. & Eckhardt, B. 2000 Transition from the Couette–Taylor system to the plane Couette system. Phys. Rev. E 61, 7227–7230.Google Scholar
Gibson, J. F.2012 Channelflow: a spectral Navier–Stokes simulator in C++. Tech. Rep., University of New Hampshire.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.CrossRefGoogle Scholar
van Gils, D. P. M., Huisman, S. G., Bruggert, G.-W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counterrotating cylinders. Phys. Rev. Lett. 106, 024502.CrossRefGoogle ScholarPubMed
van Gils, D. P. M., Huisman, S. G., Grossmann, S., Sun, C. & Lohse, D. 2012 Optimal Taylor–Couette turbulence. J. Fluid Mech. 706, 118–149.CrossRefGoogle Scholar
Hersant, F., Dubrulle, B. & Huré, J.-M. 2005 Turbulence in circumstellar disks. Astron. Astrophys. 429, 531–542.Google Scholar
Hiwatashi, K., Alfredsson, P. H., Tillmark, N. & Nagata, M. 2007 Experimental observations of instabilities in rotating plane Couette flow. Phys. Fluids 19 (4), 048103.Google Scholar
Huisman, S. G., van der Veen, R. C. A., Sun, C. & Lohse, D. 2014 Multiple states in highly turbulent Taylor–Couette flow. Nat. Commun. 5, 3820.Google Scholar
Kerr, R. M. 1996 Rayleigh number scaling in numerical convection. J. Fluid Mech. 310, 139–179.Google Scholar
Komminaho, J., Lundbladh, A. & Johansson, A. V. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–285.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Pergamon.Google Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. L. 1992 Transition to shear-driven turbulence in Couette–Taylor flow. Phys. Rev. A 46, 6390–6405.Google Scholar
Lewis, G. S. & Swinney, H. L. 1999 Velocity structure functions, scaling, and transitions in high-Reynolds-number Couette–Taylor flow. Phys. Rev. E 59, 5457–5467.Google Scholar
Lezius, D. K. & Johnston, J. P. 1976 Roll-cell instabilities in rotating laminar and trubulent channel flows. J. Fluid Mech. 77, 153–175.Google Scholar
Marcus, P. S. 1984 Simulation of Taylor–Couette flow. Part 1. Numerical methods and comparison with experiment. J. Fluid Mech. 146, 45–64.Google Scholar
Martínez-Arias, B., Peixinho, J., Crumeyrolle, O. & Mutabazi, I. 2014 Effect of the number of vortices on the torque scaling in Taylor–Couette flow. J. Fluid Mech. 748, 756–767.CrossRefGoogle Scholar
Merbold, S., Brauckmann, H. J. & Egbers, C. 2013 Torque measurements and numerical determination in differentially rotating wide gap Taylor–Couette flow. Phys. Rev. E 87, 023014.Google Scholar
Meseguer, A., Avila, M., Mellibovsky, F. & Marques, F. 2007 Solenoidal spectral formulations for the computation of secondary flows in cylindrical and annular geometries. Eur. Phys. J. Spec. Top. 146, 249–259.CrossRefGoogle Scholar
Nagata, M. 1986 Bifurcations in Couette flow between almost corotating cylinders. J. Fluid Mech. 169, 229–250.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Ostilla, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Ostilla-Mónico, R., Huisman, S. G., Jannink, T. J. G., Van Gils, D. P. M., Verzicco, R., Grossmann, S., Sun, C. & Lohse, D. 2014a Optimal Taylor–Couette flow: radius ratio dependence. J. Fluid Mech. 747, 1–29.CrossRefGoogle Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014b Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.Google Scholar
Ostilla-Mónico, R., Verzicco, R. & Lohse, D. 2015 Effects of the computational domain size on direct numerical simulations of Taylor–Couette turbulence with stationary outer cylinder. Phys. Fluids 27, 025110.CrossRefGoogle Scholar
Paoletti, M. S., van Gils, D. P. M., Dubrulle, B., Sun, C., Lohse, D. & Lathrop, D. P. 2012 Angular momentum transport and turbulence in laboratory models of Keplerian flows. Astron. Astrophys. 547 (A64), 1–11.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.Google Scholar
Pirrò, D. & Quadrio, M. 2008 Direct numerical simulation of turbulent Taylor–Couette flow. Eur. J. Mech. (B/Fluids) 27, 552–566.Google Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Ravelet, F., Delfos, R. & Westerweel, J. 2010 Influence of global rotation and Reynolds number on the large-scale features of a turbulent Taylor–Couette flow. Phys. Fluids 22 (5), 055103.CrossRefGoogle Scholar
Rayleigh, L. 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.Google Scholar
Rincon, F., Ogilvie, G. I. & Cossu, C. 2007 On self-sustaining processes in Rayleigh-stable rotating plane Couette flows and subcritical transition to turbulence in accretion disks. Astron. Astrophys. 463, 817–832.CrossRefGoogle Scholar
Salewski, M. & Eckhardt, B. 2015 Turbulent states in plane Couette flow with rotation. Phys. Fluids 27 (4), 045109.Google Scholar
Smith, G. P. & Townsend, A. A. 1982 Turbulent Couette flow between concentric cylinders at large Taylor numbers. J. Fluid Mech. 123, 187–217.Google Scholar
Suryadi, A., Segalini, A. & Alfredsson, P. H. 2014 Zero absolute vorticity: insight from experiments in rotating laminar plane Couette flow. Phys. Rev. E 89 (3), 033003.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Taylor, G. I. 1935 Distribution of velocity and temperature between concentric rotating cylinders. Proc. R. Soc. Lond. A 151, 494–512.Google Scholar
Taylor, G. I. 1936 Fluid friction between rotating cylinders. I. Torque measurements. Proc. R. Soc. Lond. A 157, 546–564.Google Scholar
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulent convection in water. Phys. Rev. E 47 (4), R2253.Google Scholar
Tritton, D. J. 1992 Stabilization and destabilization of turbulent shear flow in a rotating fluid. J. Fluid Mech. 241, 503–523.Google Scholar
Tsukahara, T. 2011 Structures and turbulent statistics in a rotating plane Couette flow. J. Phys. Conf. Ser. 318, 022024.Google Scholar
Tsukahara, T., Tillmark, N. & Alfredsson, P. H. 2010 Flow regimes in a plane Couette flow with system rotation. J. Fluid Mech. 648, 5–33.Google Scholar
Wattendorf, F. L. 1935 A study of the effect of curvature on fully developed turbulent flow. Proc. R. Soc. Lond. A 148, 565–598.Google Scholar
Wendt, F. 1933 Turbulente Strömungen zwischen zwei rotierenden konaxialen Zylindern. Ing.-Arch. 4, 577–595.Google Scholar