Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T05:25:44.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Modes and instabilities in magnetized spherical Couette flow

Published online by Cambridge University Press:  25 January 2013

A. Figueroa ,
N. Schaeffer ,
H.-C. Nataf  and
D. Schmitt
A. Figueroa
Affiliation:
ISTerre, Université de Grenoble 1, CNRS, F-38041 Grenoble, France
N. Schaeffer
Affiliation:
ISTerre, Université de Grenoble 1, CNRS, F-38041 Grenoble, France
H.-C. Nataf*
Affiliation:
ISTerre, Université de Grenoble 1, CNRS, F-38041 Grenoble, France
D. Schmitt
Affiliation:
ISTerre, Université de Grenoble 1, CNRS, F-38041 Grenoble, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Several teams have reported peculiar frequency spectra for flows in a spherical shell. To address their origin, we perform numerical simulations of the spherical Couette flow in a dipolar magnetic field, in the configuration of the 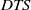$DTS$ experiment. The frequency spectra computed from time-series of the induced magnetic field display similar bumpy spectra, where each bump corresponds to a given azimuthal mode number 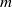$m$. The bumps appear at moderate Reynolds number (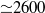${\simeq }2600$) if the time-series are long enough (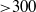${\gt }300$ rotations of the inner sphere). We present a new method that permits retrieval of the dominant frequencies for individual mode numbers 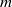$m$, and extraction of the modal structure of the full nonlinear flow. The maps of the energy of the fluctuations and the spatio-temporal evolution of the velocity field suggest that fluctuations originate in the outer boundary layer. The threshold of instability is found at 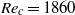${\mathit{Re}}_{c} = 1860$. The fluctuations result from two coupled instabilities: high-latitude Bödewadt-type boundary layer instability, and secondary non-axisymmetric instability of a centripetal jet forming at the equator of the outer sphere. We explore the variation of the magnetic and kinetic energies with the input parameters, and show that a modified Elsasser number controls their evolution. We can thus compare with experimental determinations of these energies and find a good agreement. Because of the dipolar nature of the imposed magnetic field, the energy of magnetic fluctuations is much larger near the inner sphere, but their origin lies in velocity fluctuations that are initiated in the outer boundary layer.

JFM classification

Boundary Layers: Boundary layer stability Geophysical and Geological Flows: Geodynamo MHD and Electrohydrodynamics: MHD turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , pp. 445 - 469
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Current address: Facultad de Ciencias, Universidad Autónoma del Estado de Morelos, 62209, Cuernavaca Morelos, México.

References

Balbus, S. A. & Hawley, J. F. 1991 A powerful local shear instability in weakly magnetized disks. 1. Linear analysis. Astrophys. J. 376 (1, Part 1), 214–222.CrossRefGoogle Scholar
Berhanu, M., Monchaux, R., Fauve, S., Mordant, N., Pétrélis, F., Chiffaudel, A., Daviaud, F., Dubrulle, B., Marié, L., Ravelet, F., Bourgoin, M., Odier, P., Pinton, J.-F. & Volk, R. 2007 Magnetic field reversals in an experimental turbulent dynamo. Europhys. Lett. 77, 59001.CrossRefGoogle Scholar
Bödewadt, U. T. 1940 Die Drehstromung über festem Grund. Z. Angew. Math. Mech. 20, 241–253.CrossRefGoogle Scholar
Brito, D., Alboussière, T., Cardin, P., Gagnière, N., Jault, D., La Rizza, P., Masson, J. P., Nataf, H. C. & Schmitt, D. 2011 Zonal shear and super-rotation in a magnetized spherical Couette-flow experiment. Phys. Rev. E 83 (6, Part 2), 066310.CrossRefGoogle Scholar
Busse, F. H. 1975 Model of geodynamo. Geophys. J. R. Astron. Soc. 42 (2), 437–459.CrossRefGoogle Scholar
Cardin, P., Brito, D., Jault, D., Nataf, H.-C. & Masson, J.-P. 2002 Towards a rapidly rotating liquid sodium dynamo experiment. Magnetohydrodynamics 38, 177–189.Google Scholar
Dormy, E., Cardin, P. & Jault, D. 1998 MHD flow in a slightly differentially rotating spherical shell, with conducting inner core, in a dipolar magnetic field. Earth Planet. Sci. Lett. 160, 15–30.CrossRefGoogle Scholar
Dumas, G. 1991 Study of spherical Couette flow via 3-D spectral simulations: large and narrow-gap flows and their transitions. PhD thesis, California Institute of Technology, Pasadena, California (USA), 231pp.Google Scholar
Elsasser, W. M. 1946 Induction effects in terrestrial magnetism part I. Theory. Phys. Rev. 69 (3–4), 106–116.CrossRefGoogle Scholar
Ferraro, V. C. A. 1937 The non-uniform rotation of the sun and its magnetic field. Mon. Not. R. Astron. Soc. 97, 458–472.CrossRefGoogle Scholar
Frick, P., Noskov, V., Denisov, S. & Stepanov, R. 2010 Direct measurement of effective magnetic diffusivity in turbulent flow of liquid sodium. Phys. Rev. Lett. 105 (18), 184502.CrossRefGoogle ScholarPubMed
Gailitis, A., Lielausis, O., Platacis, E., Dement’ev, S., Cifersons, A., Gerbeth, G., Gundrum, T., Stefani, F., Christen, M. & Will, G. 2001 Magnetic field saturation in the Riga dynamo experiment. Phys. Rev. Lett. 86, 3024–3027.CrossRefGoogle ScholarPubMed
Gauthier, G., Gondret, P. & Rabaud, M. 1999 Axisymmetric propagating vortices in the flow between a stationary and a rotating disk enclosed by a cylinder. J. Fluid Mech. 386, 105–126.CrossRefGoogle Scholar
Gissinger, C., Ji, H. & Goodman, J. 2011 Instabilities in magnetized spherical Couette flow. Phys. Rev. E 84 (2, Part 2), 026308.CrossRefGoogle ScholarPubMed
Glatzmaier, G. A. 2008 A note on ‘Constraints on deep-seated zonal winds inside Jupiter and Saturn’. Icarus 196, 665–666.CrossRefGoogle Scholar
Glatzmaier, G. A. & Roberts, P. H 1995 A three-dimensional convective dynamo solution with rotating and finitely conducting inner-core and mantle. Phys. Earth Planet. Inter. 91 (1–3), 63–75.CrossRefGoogle Scholar
Guervilly, C. & Cardin, P. 2010 Numerical simulations of dynamos generated in spherical Couette flows. Geophys. Astrophys. Fluid Dyn. 104 (2), 221–248.CrossRefGoogle Scholar
Hollerbach, R. 2009 Non-axisymmetric instabilities in magnetic spherical Couette flow. Proc. R. Soc. Lond. A 465 (2107), 2003–2013.Google Scholar
Hollerbach, R., Canet, E. & Fournier, A. 2007 Spherical Couette flow in a dipolar magnetic field. Eur. J. Mech. B 26, 729–737.CrossRefGoogle Scholar
Hollerbach, R & Skinner, S 2001 Instabilities of magnetically induced shear layers and jets. Proc. R. Soc. Lond. A 457 (2008), 785–802.CrossRefGoogle Scholar
Jault, D. 2008 Axial invariance of rapidly varying diffusionless motions in the Earth’s core interior. Phys. Earth Planet. Inter. 166, 67–76.CrossRefGoogle Scholar
Kaplan, E. J., Clark, M. M., Nornberg, M. D., Rahbarnia, K., Rasmus, A. M., Taylor, N. Z., Forest, C. B. & Spence, E. J. 2011 Reducing global turbulent resistivity by eliminating large eddies in a spherical liquid-sodium experiment. Phys. Rev. Lett. 106 (25), 254502.CrossRefGoogle Scholar
Kelley, D. H., Triana, S. A., Zimmerman, D. S. & Lathrop, D. P. 2010 Selection of inertial modes in spherical Couette flow. Phys. Rev. E 81 (2, Part 2), 026311.CrossRefGoogle ScholarPubMed
Kelley, D. H., Triana, S. A., Zimmerman, D. S., Tilgner, A. & Lathrop, D. P. 2007 Inertial waves driven by differential rotation in a planetary geometry. Geophys. Astrophys. Fluid Dyn. 101 (5–6), 469–487.CrossRefGoogle Scholar
Larmor, J. 1919 How could a rotating body such as the Sun become a magnet? Report of the British Association for the Advancement of Science 87th meeting, pp. 159–160.Google Scholar
Lathrop, D. P. & Forest, C. B. 2011 Magnetic dynamos in the lab. Phys. Today 64 (7), 40–45.CrossRefGoogle Scholar
Le Bars, M., Wieczorek, M. A., Karatekin, O., Cebron, D. & Laneuville, M. 2011 An impact-driven dynamo for the early Moon. Nature 479, 215–218.CrossRefGoogle ScholarPubMed
Lingwood, R. J. 1997 Absolute instability of the Ekman layer and related rotating flows. J. Fluid Mech. 331, 405–428.CrossRefGoogle Scholar
Liu, J., Goldreich, P. M. & Stevenson, D. J. 2008 Constraints on deep-seated zonal winds inside Jupiter and Saturn. Icarus 196, 653–664.CrossRefGoogle Scholar
Lopez, J. M., Marques, F., Rubio, A. M. & Avila, M. 2009 Crossflow instability of finite Bödewadt flows: transients and spiral waves. Phys. Fluids 21 (11), 114107.CrossRefGoogle Scholar
Matsui, H., Adams, M., Kelley, D., Triana, S. A., Zimmerman, D., Buffett, B. A. & Lathrop, D. P. 2011 Numerical and experimental investigation of shear-driven inertial oscillations in an Earth-like geometry. Phys. Earth Planet. Inter. 188, 194–202.CrossRefGoogle Scholar
Monchaux, R., Berhanu, M., Bourgoin, M., Moulin, M., Odier, P., Pinton, J.-F., Volk, R., Fauve, S., Mordant, N., Pétrélis, F., Chiffaudel, A., Daviaud, F., Dubrulle, B., Gasquet, C., Marié, L. & Ravelet, F. 2007 Generation of a magnetic field by dynamo action in a turbulent flow of liquid sodium. Phys. Rev. Lett. 98 (4), 044502.CrossRefGoogle Scholar
Moresco, P. & Alboussière, T. 2004 Stability of Bödewadt–Hartmann layers. Eur. J. Mech. B/Fluids 23 (6), 851–859.CrossRefGoogle Scholar
Nataf, H.-C., Alboussière, T., Brito, D., Cardin, P., Gagnière, N., Jault, D., Masson, J.-P. & Schmitt, D. 2006 Experimental study of super-rotation in a magnetostrophic spherical Couette flow. Geophys. Astrophys. Fluid Dyn. 100, 281–298.CrossRefGoogle Scholar
Nataf, H.-C., Alboussière, T., Brito, D., Cardin, P., Gagnière, N., Jault, D. & Schmitt, D. 2008 Rapidly rotating spherical Couette flow in adipolar magnetic field: an experimental study of the mean axisymmetric flow. Phys. Earth Planet. Inter. 170, 60–72.CrossRefGoogle Scholar
Noir, J., Hemmerlin, F., Wicht, J., Baca, S. M. & Aurnou, J. M. 2009 An experimental and numerical study of librationally driven flow in planetary cores and subsurface oceans. Phys. Earth Planet. Inter. 173 (1–2), 141–152.CrossRefGoogle Scholar
Nornberg, M. D., Ji, H., Schartman, E., Roach, A. & Goodman, J. 2010 Observation of magnetocoriolis waves in a liquid metal Taylor–Couette experiment. Phys. Rev. Lett. 104 (7), 074501.CrossRefGoogle Scholar
Rieutord, M., Triana, S. A., Zimmerman, D. S. & Lathrop, D. P. 2012 Excitation of inertial modes in an experimental spherical Couette flow. Phys. Rev. E 86 (2, Part 2), 026304.CrossRefGoogle Scholar
Rieutord, M. & Valdettaro, L. 1997 Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99.CrossRefGoogle Scholar
Roach, A. H., Spence, E. J., Gissinger, C., Edlund, E. M., Sloboda, P., Goodman, J. & Ji, H. 2012 Observation of a free-Shercliff-layer instability in cylindrical geometry. Phys. Rev. Lett. 108 (15), 154502.CrossRefGoogle ScholarPubMed
Saric, W. S. 1994 Görtler vortices. Annu. Rev. Fluid Mech. 26, 379–409.CrossRefGoogle Scholar
Savas, Ö. M. 1987 Stability of Bödewadt flow. J. Fluid Mech. 183, 77–94.CrossRefGoogle Scholar
Schaeffer, N. 2012 Efficient spherical harmonic transforms aimed at pseudo-spectral numerical simulations. ArXiv e-prints 1202.6522.Google Scholar
Schmitt, D., Alboussière, T., Brito, D., Cardin, P., Gagnière, N., Jault, D. & Nataf, H.-C. 2008 Rotating spherical Couette flow in a dipolar magnetic field: experimental study of magneto-inertial waves. J. Fluid Mech. 604, 175–197.CrossRefGoogle Scholar
Schmitt, D., Cardin, P., La Rizza, P. & Nataf, H.-C. 2013 Magneto-Coriolis waves in a spherical Couette flow experiment. Eur. J. Mech. B/Fluids 37, 10–22.CrossRefGoogle Scholar
Schouveiler, L., Le Gal, P. & Chauve, MP 2001 Instabilities of the flow between a rotating and a stationary disk. J. Fluid Mech. 443, 329–350.CrossRefGoogle Scholar
Sisan, D. R., Mujica, N., Tillotson, W. A., Huang, Y.-M., Dorland, W., Hassam, A. B., Antonsen, T. M. & Lathrop, D. P. 2004 Experimental observation and characterization of the magnetorotational instability. Phys. Rev. Lett. 93 (11), 114502.CrossRefGoogle ScholarPubMed
Starchenko, S. V. 1997 Magnetohydrodynamics of a viscous spherical shell in a strong potential field. J. Expl Theor. Phys. 85 (6), 1125–1137.CrossRefGoogle Scholar
Stieglitz, R. & Müller, U. 2001 Experimental demonstration of a homogeneous two-scale dynamo. Phys. Fluids 13, 561–564.CrossRefGoogle Scholar

Figueroa et al. supplementary movie

Map view of the time evolution of the azimuthal velocity uφ beneath the surface of the outer sphere (r = 0.95) in the reference numerical simulation (Pm = 10-3, Re = 2 611 and Λ = 3.4 _ 10-2). At the origin time, the fluid is at rest and the rotation rate of the inner sphere is set to f. Time t is measured in rotation periods of the inner sphere. There are 6 frames per turn and the movie lasts 100 turns. Note that the first instabilities appear at the equator and are axisymmetric. After about 24 turns, nonaxisymmetric instabilities show up.

Download Figueroa et al. supplementary movie(Video)
Video 18 MB

Figueroa et al. supplementary movie

Time evolution of the angular velocity ω = uφ/s in a meridional plane (φ = 0) for the same simulation as in movie 1.

Download Figueroa et al. supplementary movie(Video)
Video 13.8 MB