Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T10:27:53.720Z Has data issue: false hasContentIssue false
  • English
  • Français

A model to predict the oscillation frequency for drops pinned on a vertical planar surface

Published online by Cambridge University Press:  08 October 2021

J. Sakakeeny Open the ORCID record for J. Sakakeeny [Opens in a new window] ,
C. Deshpande ,
S. Deb ,
J.L. Alvarado  and
Y. Ling Open the ORCID record for Y. Ling [Opens in a new window]
J. Sakakeeny
Affiliation:
Department of Mechanical Engineering, Baylor University, Waco, TX 76643, USA
C. Deshpande
Affiliation:
Department of Mechanical Engineering, Texas A&M University, College Station, TX 77843, USA
S. Deb
Affiliation:
Department of Mechanical Engineering, Texas A&M University, College Station, TX 77843, USA
J.L. Alvarado
Affiliation:
Department of Mechanical Engineering, Texas A&M University, College Station, TX 77843, USA Department of Engineering Technology and Industrial Distribution, Texas A&M University, College Station, TX 77843, USA
Y. Ling*
Affiliation:
Department of Mechanical Engineering, Baylor University, Waco, TX 76643, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

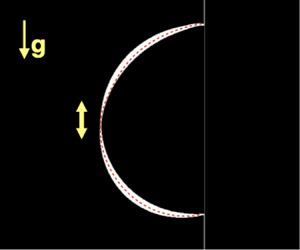
Accurate prediction of the natural frequency for the lateral oscillation of a liquid drop pinned on a vertical planar surface is important to many drop applications. The natural oscillation frequency, normalized by the capillary frequency, is mainly a function of the equilibrium contact angle and the Bond number ($Bo$), when the contact lines remain pinned. Parametric numerical and experimental studies have been performed to establish a comprehensive understanding of the oscillation dynamics. An inviscid model has been developed to predict the oscillation frequency for wide ranges of $Bo$ and the contact angle. The model reveals the scaling relation between the normalized frequency and $Bo$, which is validated by the numerical simulation results. For a given equilibrium contact angle, the lateral oscillation frequency decreases with $Bo$, implying that resonance frequencies will be magnified if the drop oscillations occur in a reduced gravity environment.

JFM classification

Interfacial Flows (free surface): Contact lines Drops and Bubbles: Drops
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 928 , 10 December 2021 , A28
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Afkhami, S., Buongiorno, J., Guion, A., Popinet, S., Saade, Y., Scardovelli, R. & Zaleski, S. 2018 Transition in a numerical model of contact line dynamics and forced dewetting. J. Comput. Phys. 374, 1061–1093.CrossRefGoogle Scholar
Afkhami, S. & Bussmann, M. 2009 Height functions for applying contact angles to 3d VOF simulations. Intl J. Numer. Meth. Fluids 61 (8), 827–847.CrossRefGoogle Scholar
Boreyko, J.B. & Chen, C.-H. 2009 a Restoring superhydrophobicity of lotus leaves with vibration-induced dewetting. Phys. Rev. Lett. 103, 174502.CrossRefGoogle ScholarPubMed
Boreyko, J.B. & Chen, C.-H. 2009 b Self-propelled dropwise condensate on superhydrophobic surfaces. Phys. Rev. Lett. 103, 184501.CrossRefGoogle ScholarPubMed
Bostwick, J.B. & Steen, P.H. 2014 Dynamics of sessile drops. Part 1. Inviscid theory. J. Fluid Mech. 760, 5–38.CrossRefGoogle Scholar
Celestini, F. & Kofman, R. 2006 Vibration of submillimeter-size supported droplets. Phys. Rev. E 73, 041602.CrossRefGoogle ScholarPubMed
Chang, C.-T., Bostwick, J.B., Daniel, S. & Steen, P.H. 2015 Dynamics of sessile drops. Part 2. Experiment. J. Fluid Mech. 768, 442–467.CrossRefGoogle Scholar
Dai, X., Sun, N., Nielsen, S.O., Stogin, B.B., Wang, J., Yang, S. & Wong, T.-S. 2018 Hydrophilic directional slippery rough surfaces for water harvesting. Sci. Adv. 4, eaaq0919.CrossRefGoogle ScholarPubMed
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Noblin, X., Buguin, A. & Brochard-Wyart, F. 2004 Vibrated sessile drops: transition between pinned and mobile contact line oscillations. Eur. Phys. J. E 14, 395–404.CrossRefGoogle ScholarPubMed
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228 (16), 5838–5866.CrossRefGoogle Scholar
Prosperetti, A. 1980 Normal-mode analysis for the oscillations of a viscous-liquid drop in an immiscible liquid. J. Méc. 19, 149–182.Google Scholar
Sakakeeny, J. & Ling, Y. 2020 Natural oscillations of a sessile drop on flat surfaces with mobile contact lines. Phys. Rev. Fluids 5, 123604.CrossRefGoogle Scholar
Sakakeeny, J. & Ling, Y. 2021 Numerical study of natural oscillations of supported drops with free and pinned contact lines. Phys. Fluids 33, 062109.CrossRefGoogle Scholar
Scardovelli, R. & Zaleski, S. 1999 Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 31, 567–603.CrossRefGoogle Scholar
Sharp, J.S., Farmer, D.J. & Kelly, J. 2011 Contact angle dependence of the resonant frequency of sessile water droplets. Langmuir 27, 9367–9371.CrossRefGoogle ScholarPubMed
Snoeijer, J.H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.CrossRefGoogle Scholar
Strani, M. & Sabetta, F. 1984 Free vibrations of a drop in partial contact with a solid support. J. Fluid Mech. 141, 233–247.CrossRefGoogle Scholar
Strani, M. & Sabetta, F. 1988 Viscous oscillations of a supported drop in an immiscible fluid. J. Fluid Mech. 189, 397–421.CrossRefGoogle Scholar
Yao, C.W., Garvin, T.P., Alvarado, J.L., Jacobi, A.M., Jones, B.G. & Marsh, C.P. 2012 Droplet contact angle behavior on a hybrid surface with hydrophobic and hydrophilic properties. Appl. Phys. Lett. 101, 111605.CrossRefGoogle Scholar
Yao, C.-W., Lai, C.-L., Alvarado, J.L., Zhou, J., Aung, K.T. & Mejia, J.E. 2017 Experimental study on effect of surface vibration on micro textured surfaces with hydrophobic and hydrophilic materials. Appl. Surf. Sci. 412, 45–51.CrossRefGoogle Scholar