Published online by Cambridge University Press: 19 February 2013
Navier–Stokes simulations of the agitation generated by a homogeneous swarm of high-Reynolds-number rising bubbles are performed. The bubbles are modelled by fixed momentum sources of finite size randomly distributed in a uniform flow. The mesh grid is regular with a spacing close to the bubble size. This allows us to simulate a swarm of a few thousand bubbles in a computational domain of a hundred bubble diameters, which corresponds to a gas volume fraction  $\alpha $ from 0.6 % to 4 %. The small-scale disturbances close to the bubbles are not resolved but the wakes are correctly described from a distance of a few diameters. This simple model reproduces well all the statistical properties of the vertical velocity fluctuations measured in previous experiments: scaling as
$\alpha $ from 0.6 % to 4 %. The small-scale disturbances close to the bubbles are not resolved but the wakes are correctly described from a distance of a few diameters. This simple model reproduces well all the statistical properties of the vertical velocity fluctuations measured in previous experiments: scaling as 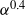 ${\alpha }^{0. 4} $, self-similar probability density functions and power spectral density including a subrange evolving as the power
${\alpha }^{0. 4} $, self-similar probability density functions and power spectral density including a subrange evolving as the power 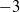 $- 3$ of the wavenumber
$- 3$ of the wavenumber 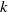 $k$. It can therefore be concluded that bubble-induced agitation mainly results from wake interactions. Considering the flow in a frame that is fixed relative to the bubbles, the combined use of both time and spatial averaging makes it possible to distinguish two contributions to the liquid fluctuations. The first is the spatial fluctuations that are the consequence of the bubble mean wakes. The second corresponds to the temporal fluctuations that are the result of the development of a flow instability. Note that the latter is not due to the destabilization of individual bubble wakes, since a computation with a single bubble leads to a steady flow. It is a collective instability of the randomly distributed bubble wakes. The spectrum of the time fluctuations shows a peak around a frequency
$k$. It can therefore be concluded that bubble-induced agitation mainly results from wake interactions. Considering the flow in a frame that is fixed relative to the bubbles, the combined use of both time and spatial averaging makes it possible to distinguish two contributions to the liquid fluctuations. The first is the spatial fluctuations that are the consequence of the bubble mean wakes. The second corresponds to the temporal fluctuations that are the result of the development of a flow instability. Note that the latter is not due to the destabilization of individual bubble wakes, since a computation with a single bubble leads to a steady flow. It is a collective instability of the randomly distributed bubble wakes. The spectrum of the time fluctuations shows a peak around a frequency 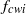 ${f}_{cwi} $, which is independent of
${f}_{cwi} $, which is independent of  $\alpha $. From the present results it is possible to determine the origin of the overall properties of the total fluctuations observed in the experiments. The scaling of the velocity fluctuation as
$\alpha $. From the present results it is possible to determine the origin of the overall properties of the total fluctuations observed in the experiments. The scaling of the velocity fluctuation as 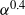 ${\alpha }^{0. 4} $ is a combination of the scalings of the spatial and temporal fluctuations, which are different from each other. As the time fluctuations are symmetric in the vertical direction, the asymmetry of the probability density function of the vertical velocity comes from that of the spatial fluctuations. Both contributions exhibit a
${\alpha }^{0. 4} $ is a combination of the scalings of the spatial and temporal fluctuations, which are different from each other. As the time fluctuations are symmetric in the vertical direction, the asymmetry of the probability density function of the vertical velocity comes from that of the spatial fluctuations. Both contributions exhibit a  ${k}^{- 3} $ spectral behaviour around the same range of wavenumbers, which explains why it is observed regardless of the nature of the dominant contribution.
${k}^{- 3} $ spectral behaviour around the same range of wavenumbers, which explains why it is observed regardless of the nature of the dominant contribution.