Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T10:36:49.720Z Has data issue: false hasContentIssue false
  • English
  • Français

A measure of scale-dependent asymmetry in turbulent boundary layer flows: scaling and Reynolds number similarity

Published online by Cambridge University Press:  24 May 2016

Arvind Singh ,
Kevin B. Howard  and
Michele Guala
Arvind Singh*
Affiliation:
Department of Civil, Environmental and Construction Engineering, University of Central Florida, Orlando, FL 32816, USA
Kevin B. Howard
Affiliation:
St. Anthony Falls Laboratory, Department of Civil, Environmental and Geo-Engineering, University of Minnesota, Minneapolis, MN 55414, USA
Michele Guala
Affiliation:
St. Anthony Falls Laboratory, Department of Civil, Environmental and Geo-Engineering, University of Minnesota, Minneapolis, MN 55414, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The distribution of temporal scale-dependent streamwise velocity increments is investigated in turbulent boundary layer flows at laboratory and atmospheric Reynolds numbers, using the St. Anthony Falls Laboratory wind tunnel and the Surface Layer Turbulence and Environmental Science Test dataset, respectively. The third-order moments of velocity increments, or asymmetry index 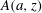$A(a,z)$, is computed for varying wall distance $z$ and time scale separation $a$, where it was observed to leave a robust, distinct signature in the form of a hump, independent of Reynolds number and located across the inertial range. The hump is observed in wall region limited to 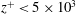$z^{+}<5\times 10^{3}$, with a tendency to shift towards smaller time scales as the surface is approached ($z^{+}<70$). Comparing the two datasets, the hump, and its location, are found to obey inner wall scaling and is regarded as a genuine feature of the canonical turbulent boundary layer. The magnitude cumulant analysis of the scale-dependent velocity increments further reveals that intermittency is also enhanced near the wall, in the same flow region where the asymmetry signature was observed. The combination of asymmetry and intermittency is inferred to point at non-local energy transfer and scale coupling across a range of scales. From a turbulent structure perspective, such non-local energy transfer can be seen as the result of strong scale-interaction processes between outer scale motions in the logarithmic layer impacting and distorting smaller scales at the wall, through abrupt energy transfer across scales bypassing the typical energy cascade of the inertial range.

JFM classification

Turbulent Flows: Intermittency
Type
Papers
Information
Journal of Fluid Mechanics , Volume 797 , 25 June 2016 , pp. 549 - 563
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Orlandi, P. & Romano, G. P. 1998 Scaling of longitudinal velocity increments in a fully developed turbulent channel flow. Phys. Fluids 10, 3239.CrossRefGoogle Scholar
Basu, S., Foufoula-Georgiou, E., Lashermes, B. & Arnéodo, A. 2007 Estimating intermittency exponent in neutrally stratified atmospheric surface layer flows: a robust framework based on magnitude cumulant and surrogate analyses. Phys. Fluids 19, 115102.Google Scholar
Benzi, R., Ciliberto, S., Tripiccione, C., Baudet, C., Massaioli, F. & Succi, F. 1993 Extended self similarity in turbulent flows. Phys Rev. E 48, R29–R32.Google Scholar
Boettcher, F., Renner, C. H., Waldl, H. P. & Peinke, J. 2003 On the statistics of wind gusts. Boundary-Layer Meteorol. 108, 163–173.Google Scholar
Carper, M. & Porté-Agel, F. 2008 Subfilter-scale fluxes over a surface roughness transition. Part I: measured fluxes and energy transfer rates. Boundary-Layer Meteorol. 126, 157–179.CrossRefGoogle Scholar
Chamorro, L. P. & Porté-Agel, F. 2009 A wind-tunnel investigation of wind-turbine wakes: boundary-layer turbulence effects. Boundary-Layer Meteorol. 132, 129–149.CrossRefGoogle Scholar
Chevillard, L., Roux, S. G., Leveque, E., Mordant, N., Pinton, J.-F. & Arneodo, A. 2005 Intermittency of velocity time increments in turbulence. Phys. Rev. Lett. 95, 064501.Google Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Delour, J., Muzy, J. F. & Arnéodo, A. 2001 Intermittency of 1D velocity spatial profiles in turbulence: a magnitude cumulant analysis. Eur. Phys. J. B 23, 243–248.Google Scholar
Frisch, U. 1995 Turbulence, the Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2010 Intermittency in the atmospheric surface layer: unresolved or slowly varying? Physica D 239 (14), 1251–1257.Google Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2011 Interactions within the turbulent boundary layer at high Reynolds number. J. Fluid Mech. 666, 573–604.Google Scholar
Jimenez, J. 2000 Intermittency and cascades. J. Fluid Mech. 409, 99–120.CrossRefGoogle Scholar
Howard, K. B., Hu, J. S., Chamorro, L. P. & Guala, M. 2015a Characterizing the response of a wind-turbine model under complex inflow conditions. Wind Energy 18 (4), 729–743.CrossRefGoogle Scholar
Howard, K. B., Singh, A., Sotiropoulos, F. & Guala, M. 2015b On the statistics of wind turbine wake meandering: an experimental investigation. Phys. Fluids 27 (7), 075103.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Hutchins, N. & Marusic, I. 2007a Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Hutchins, N. & Marusic, I. 2007b Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Keylock, C. J., Singh, A. & Foufoula-Georgiou, E. 2013 The influence of migrating bed forms on the velocity–intermittency structure of turbulent flow over a gravel bed. Geophys. Res. Lett. 40, 1351–1355.Google Scholar
Keylock, C. J., Singh, A., Venditti, J. G. & Foufoula-Georgiou, E. 2014 Robust classification for the joint velocity–intermittency structure of turbulent flow over fixed and mobile bedforms. Earth Surf. Process. Landf. 39, 1717–1728.Google Scholar
Kolmogorov, A. N. 1941 Local structure of turbulence in an incompressible liquid for very large Reynolds numbers. C. R. Acad. Sci. USSR 30, 301–305.Google Scholar
Kholmyansky, M., Moriconi, L. & Tsinober, A. 2007 Large scale intermittency in the atmospheric boundary layer. Phys. Rev. E 76, 026307.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.CrossRefGoogle Scholar
Kraichnan, R. H. 1974 On Kolmogorov inertial range theories. J. Fluid Mech. 62 (2), 306–330.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Laval, J.-P., Dubrulle, B. & Nazarenko, S. 2001 Nonlocality and intermittency in three-dimensional turbulence. Phys. Fluids 13, 1995.Google Scholar
Liu, L., Hu, F., Cheng, X.-L. & Song, L.-L. 2010 Probability density functions of velocity increments in the atmospheric boundary layer. Boundary-Layer Meteorol. 134, 243–255.Google Scholar
Malecot, Y., Auriault, C., Kahalerras, H., Gagne, Y., Chanal, O., Chabaud, B. & Castaing, B. 2000 A statistical estimator of turbulence intermittency in physical and numerical experiments. Eur. Phys. J. B 16, 549–561.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mazellier, N. & Vassilicos, J. C. 2008 The turbulence dissipation constant is not universal because of its universal dependence on large-scale flow topology. Phys. Fluids 20, 015101.Google Scholar
Menevau, C. & Sreenivasan, K. R. 1991 The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 224, 429–484.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13, 692–701.Google Scholar
Metzger, M., McKeon, B. J. & Holmes, H. 2007 The near-neutral atmospheric surface layer: turbulence and non-stationarity. Phil. Trans. R. Soc. Lond. A 365, 859–876.Google Scholar
Mininni, P. D., Alexakis, A. & Pouquet, A. 2006 Large-scale flow effects, energy transfer, and self-similarity on turbulence. Phys. Rev. E 74, 016303.Google Scholar
Morrison, J. F. 2007 The interaction between inner and outer regions of turbulent wall-bounded flows. Phil. Trans. R. Soc. Lond. A 365, 683–698.Google Scholar
Onorato, M., Camussi, R. & Iuso, G. 2000 Small scale intermittency and bursting in a turbulent channel flow. Phys. Rev. E 61 (2), 1446–1454.Google Scholar
Osterlund, J. M.1999 Experimental studies of zero pressure-gradient turbulent boundary-layer flow. PhD thesis, Department of Mechanics, Royal Institute of Technology, Stockholm.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Poggi, D., Porporato, A., Ridolfi, L., Albertson, J. D. & Katul, G. 2004 Interaction between large and small scales in the canopy sublayer. Geophys. Res. Lett. 31 (5), L05102.Google Scholar
Ruiz-Chavarria, G., Ciliberto, S., Baudet, C. & Lévêqueb, E. 2000 Scaling properties of the streamwise component of velocity in a turbulent boundary layer. Physica D 141, 183–198.Google Scholar
Schertzer, D., Lovejoy, S., Schmitt, F., Chiguirinskaya, Y. & Marsan, D. 1997 Multifractal cascade dynamics and turbulent intermittency. Fractals 5, 427–471.Google Scholar
de Silva, C. M., Marusic, I., Woodcock, J. D. & Meneveau, C. 2015 Scaling of second- and higher-order structure functions in turbulent boundary layers. J. Fluid Mech. 769, 654–686.Google Scholar
Singh, A., Fienberg, K., Jerolmack, D. J., Marr, J. & Foufoula-Georgiou, E. 2009 Experimental evidence for statistical scaling and intermittency in sediment transport rates. J. Geophys. Res. 114, F01025.Google Scholar
Singh, A., Foufoula-Georgiou, E., Porté-Agel, F. & Wilcock, P. R. 2012 Coupled dynamics of the co-evolution of bed topography, flow turbulence and sediment transport in an experimental flume. J. Geophys. Res. 117, F04016.Google Scholar
Singh, A., Howard, K. B. & Guala, M. 2014 On the homogenization of turbulent flow structures in the wake of a model wind turbine. Phys. Fluids 26 (2), 025103.Google Scholar
Singh, A., Lanzoni, S., Wilcock, P. R. & Foufoula-Georgiou, E. 2011 Multi-scale statistical characterization of migrating bedforms in gravel and sand bed rivers. Water Resour. Res. 47, W12526.Google Scholar
Singh, A., Porté-Agel, F. & Foufoula-Georgiou, E. 2010 On the influence of gravel bed dynamics on velocity power spectra. Water Resour. Res. 46, W04509.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Toschi, F., Leveque, E. & Ruiz-Chavarria, G. 2000 Shear effects in nonhomogeneous turbulence. Phys. Rev. Lett. 85 (7), 1436–1439.Google Scholar
Venugopal, V., Roux, S. G., Foufoula-Georgiou, E. & Arnéodo, A. 2006 Revisiting multifractality of high-resolution temporal rainfall using a wavelet-based formalism. Water Resour. Res. 42, W06D14.Google Scholar
Warhaft, Z. 2002 Turbulence in nature and in the laboratory. Proc. Natl Acad. Sci. USA 99 (Suppl. 1), 2481–2486.Google Scholar
Yeung, P. K., Brasseur, J. G. & Wang, Q. 1995 Dynamics of direct large-small scale couplings in coherently forced turbulence: concurrent physical- and Fourier-space views. J. Fluid Mech. 283, 43–95.Google Scholar