Article contents
Marangoni-enhanced capillary wetting in surfactant-driven superspreading
Published online by Cambridge University Press: 14 September 2018
Abstract
Superspreading is a phenomenon such that a drop of a certain class of surfactant on a substrate can spread with a radius that grows linearly with time much faster than the usual capillary wetting. Its origin, in spite of many efforts, is still not fully understood. Previous modelling and simulation studies (Karapetsas et al. J. Fluid Mech., vol. 670, 2011, pp. 5–37; Theodorakis et al. Langmuir, vol. 31, 2015, pp. 2304–2309) suggest that the transfer of the interfacial surfactant molecules onto the substrate in the vicinity of the contact line plays a crucial role in superspreading. Here, we construct a detailed theory to elaborate on this idea, showing that a rational account for superspreading can be made using a purely hydrodynamic approach without involving a specific surfactant structure or sorption kinetics. Using this theory it can be shown analytically, for both insoluble and soluble surfactants, that the curious linear spreading law can be derived from a new dynamic contact line structure due to a tiny surfactant leakage from the air–liquid interface to the substrate. Such a leak not only establishes a concentrated Marangoni shearing toward the contact line at a rate much faster than the usual viscous stress singularity, but also results in a microscopic surfactant-devoid zone in the vicinity of the contact line. The strong Marangoni shearing then turns into a local capillary force in the zone, making the contact line in effect advance in a surfactant-free manner. This local Marangoni-driven capillary wetting in turn renders a constant wetting speed governed by the de Gennes–Cox–Voinov law and hence the linear spreading law. We also determine the range of surfactant concentration within which superspreading can be sustained by local surfactant leakage without being mitigated by the contact line sweeping, explaining why only limited classes of surfactants can serve as superspreaders. We further show that spreading of surfactant spreaders can exhibit either the 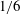 $1/6$ or
$1/6$ or 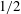 $1/2$ power law, depending on the ability of interfacial surfactant to transfer/leak to the bulk/substrate. All these findings can account for a variety of results seen in experiments (Rafai et al. Langmuir, vol. 18, 2002, pp. 10486–10488; Nikolov & Wasan, Adv. Colloid Interface Sci., vol. 222, 2015, pp. 517–529) and simulations (Karapetsas et al. 2011). Analogy to thermocapillary spreading is also made, reverberating the ubiquitous role of the Marangoni effect in enhancing dynamic wetting driven by non-uniform surface tension.
$1/2$ power law, depending on the ability of interfacial surfactant to transfer/leak to the bulk/substrate. All these findings can account for a variety of results seen in experiments (Rafai et al. Langmuir, vol. 18, 2002, pp. 10486–10488; Nikolov & Wasan, Adv. Colloid Interface Sci., vol. 222, 2015, pp. 517–529) and simulations (Karapetsas et al. 2011). Analogy to thermocapillary spreading is also made, reverberating the ubiquitous role of the Marangoni effect in enhancing dynamic wetting driven by non-uniform surface tension.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 18
- Cited by



