Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T04:29:35.894Z Has data issue: false hasContentIssue false
  • English
  • Français

Magnetic knot cascade via the stepwise reconnection of helical flux tubes

Published online by Cambridge University Press:  18 February 2021

Jinhua Hao Open the ORCID record for Jinhua Hao [Opens in a new window]  and
Yue Yang Open the ORCID record for Yue Yang [Opens in a new window]
Jinhua Hao
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing100871, PR China
Yue Yang*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing100871, PR China Center for Applied Physics and Technology, and Beijing Innovation Center for Engineering Science and Advanced Technology, Peking University, Beijing100871, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

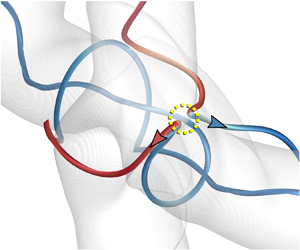
We report a knot cascade of magnetic field lines through the stepwise reconnection of a pair of orthogonal helical flux tubes with opposite chirality. The magnetic-surface field is developed to identify the evolution of flux tubes and pinpoint the reconnection region. We find that the incipient X-type magnetic reconnection generates antiparallel U-shaped field lines moving in opposite directions away from the plasmoid. This reconnection is characterized by the decay of the magnetic flux through the diagonal symmetric planes. Subsequently, overhand magnetic knots are tied via the secondary reconnection, coinciding with the notable conversion from magnetic energy to kinetic energy. The knotted field lines are then rotated and stretched in the plasmoid by the vortical-like local motion induced by the magnetic knots themselves via the Lorentz force. This nonlinear evolution triggers the tertiary reconnection to form double overhand knots, and then further reconnections to produce more complex knots. From field lines extracted at different times, the knot cascade via the sequence of reconnections in a finite time period is quantified by the increment of the minimum crossing number and the migration of the probability density function of the Alexander–Briggs notation. Finally, the knot cascade slows down and then terminates due to resistive and viscous dissipations.

JFM classification

Mathematical Foundations: Topological fluid dynamics MHD and Electrohydrodynamics: Plasmas
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 912 , 10 April 2021 , A48
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alekseenko, S.V., Kuibin, P.A., Shtork, S.I., Skripkin, S.G. & Tsoy, M.A. 2016 Vortex reconnection in a swirling flow. JETP Lett. 103, 455–459.CrossRefGoogle Scholar
Alexander, J.W. & Briggs, G.B. 1926 On types of knotted curves. Ann. Maths 28, 562–586.CrossRefGoogle Scholar
Arrayás, M., Bouwmeester, D. & Trueba, J.L. 2017 Knots in electromagnetism. Phys. Rep. 667, 1–61.CrossRefGoogle Scholar
Arrayás, M. & Trueba, J.L. 2014 A class of non-null toroidal electromagnetic fields and its relation to the model of electromagnetic knots. J. Phys. A 48, 025203.CrossRefGoogle Scholar
Beckers, J.M. & Schröter, E.H. 1968 The intensity, velocity and magnetic structure of a sunspot region. Sol. Phys. 4, 142–164.CrossRefGoogle Scholar
Berger, M.A. 1997 Magnetic helicity in a periodic domain. J. Geophys. Res. Space Phys. 102, 2637–2644.CrossRefGoogle Scholar
Berger, M.A. & Field, G.B. 1984 The topological properties of magnetic helicity. J. Fluid Mech. 147, 133–148.CrossRefGoogle Scholar
Berger, M.A., Ricca, R.L., Kauffman, L.H., Khesin, B., Moffatt, H.K. & Sumners, D.L. 2009 Lectures on Topological Fluid Mechanics. Springer.CrossRefGoogle Scholar
Buck, D. & Ishihara, K. 2015 Coherent band pathways between knots and links. J. Knot Theory Ramif. 24, 1550006.CrossRefGoogle Scholar
Candelaresi, S. & Brandenburg, A. 2011 Decay of helical and nonhelical magnetic knots. Phys. Rev. E 84, 016406.CrossRefGoogle ScholarPubMed
Cooper, R.G., Mesgarnezhad, M., Baggaley, A.W. & Barenghi, C.F. 2019 Knot spectrum of turbulence. Sci. Rep. 9, 10545.CrossRefGoogle ScholarPubMed
Dahlburg, R.B., Antiochos, S.K. & Norton, D. 1997 Magnetic flux tube tunneling. Phys. Rev. E 56, 2094–2103.CrossRefGoogle Scholar
Davidson, P.A. 2001 An Introduction to Magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
Del Sordo, F., Candelaresi, S. & Brandenburg, A. 2010 Magnetic-field decay of three interlocked flux rings with zero linking number. Phys. Rev. E 81, 036401.CrossRefGoogle ScholarPubMed
Farrugia, C.J., et al. 1999 A uniform-twist magnetic flux rope in the solar wind. AIP Conf. Proc. 471, 745–748.CrossRefGoogle Scholar
Finkelstein, D. & Weil, D. 1978 Magnetohydrodynamic kinks in astrophysics. Intl J. Theor. Phys. 17, 201–217.CrossRefGoogle Scholar
Gold, T. & Hoyle, F. 1960 On the origin of solar flares. Mon. Not. R. Astron. Soc. 120, 89–105.CrossRefGoogle Scholar
Gottlieb, S. & Shu, C.-W. 1998 Total variation diminishing Runge–Kutta schemes. Maths Comput. 67, 73–85.CrossRefGoogle Scholar
Hall, D.S., Ray, M.W., Tiurev, K., Ruokokoski, E., Gheorghe, A.H. & Möttönen, M. 2016 Tying quantum knots. Nat. Phys. 12, 478–483.CrossRefGoogle Scholar
Hao, J., Xiong, S. & Yang, Y. 2019 Tracking vortex surfaces frozen in the virtual velocity in non-ideal flows. J. Fluid Mech. 863, 513–544.CrossRefGoogle Scholar
Hesse, M., Forbes, T.G. & Birn, J. 2005 On the relation between reconnected magnetic flux and parallel electric fields in the solar corona. Astrophys. J. 631, 1227–1238.CrossRefGoogle Scholar
Hoste, J., Thistlethwaite, M. & Weeks, J. 1998 The first 1,701,936 knots. Math. Intell. 20, 33–48.CrossRefGoogle Scholar
Jiang, G.S. & Shu, C.-W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228.CrossRefGoogle Scholar
Kauffman, L.H. 2001 Knots and Physics. World Scientific.CrossRefGoogle Scholar
Kerr, R.M. 2018 Trefoil knot timescales for reconnection and helicity. Fluid Dyn. Res. 50, 011422.CrossRefGoogle Scholar
Kida, S. & Takaoka, M. 1994 Vortex reconnection. Annu. Rev. Fluid Mech. 26, 169–189.CrossRefGoogle Scholar
Kivotides, D. 2018 Interactions between vortex tubes and magnetic-flux rings at high kinetic and magnetic Reynolds numbers. Phys. Rev. Fluids 3, 033701.CrossRefGoogle Scholar
Kleckner, D. & Irvine, W.T.M. 2013 Creation and dynamics of knotted vortices. Nat. Phys. 9, 253–258.CrossRefGoogle Scholar
Kleckner, D., Kauffman, L.H. & Irvine, W.T.M. 2016 How superfluid vortex knots untie. Nat. Phys. 12, 650–655.CrossRefGoogle Scholar
Klotz, A.R., Soh, B.W. & Doyle, P.S. 2018 Motion of knots in DNA stretched by elongational fields. Phys. Rev. Lett. 120, 188003.CrossRefGoogle ScholarPubMed
Knizhnik, K.J., Linton, M.G. & Devore, C.R. 2018 The role of twist in kinked flux rope emergence and delta-spot formation. Astrophys. J. 864, 89.CrossRefGoogle Scholar
Kopp, R.A. & Pneuman, G.W. 1976 Magnetic reconnection in the corona and the loop prominence phenomenon. Sol. Phys. 50, 85–98.CrossRefGoogle Scholar
Kuei, S., Słowicka, A.M., Ekiel-Jeżewska, M.L., Wajnryb, E. & Stone, H.A. 2015 Dynamics and topology of a flexible chain: knots in steady shear flow. New J. Phys. 17, 053009.CrossRefGoogle Scholar
Lau, Y.T. & Finn, J.M. 1996 Magnetic reconnection and the topology of interacting twisted flux tubes. Phys. Plasmas 3, 3983–3997.CrossRefGoogle Scholar
Lin, J. & Forbes, T.G. 2000 Effects of reconnection on the coronal mass ejection process. J. Geophys. Res. 105, 2375–2392.CrossRefGoogle Scholar
Linton, M.G. & Antiochos, S.K. 2005 Magnetic flux tube reconnection: tunneling versus slingshot. Astrophys. J. 625, 506–521.CrossRefGoogle Scholar
Linton, M.G., Dahlburg, R.B. & Antiochos, S.K. 2001 Reconnection of twisted flux tubes as a function of contact angle. Astrophys. J. 553, 905–921.CrossRefGoogle Scholar
Liu, X. & Ricca, R.L. 2015 On the derivation of the HOMFLYPT polynomial invariant for fluid knots. J. Fluid Mech. 773, 34–48.CrossRefGoogle Scholar
Liu, X. & Ricca, R.L. 2016 Knots cascade detected by a monotonically decreasing sequence of values. Sci. Rep. 6, 24118.CrossRefGoogle ScholarPubMed
Liu, X., Ricca, R.L. & Li, X.F. 2020 Minimal unlinking pathways as geodesics in knot polynomial space. Commun. Phys. 3, 136.CrossRefGoogle Scholar
Melander, M.V. & Hussain, F 1988 Cut-and-connect of two antiparallel vortex tubes. In Proceedings of the 1988 Summer Program, Center for Turbulence Research, pp. 257–286. Stanford University.Google Scholar
Mesgarnezhad, M., Cooper, R.G., Baggaley, A.W. & Barenghi, C.F. 2017 Helicity and topology of a small region of quantum vorticity. Fluid Dyn. Res. 50, 011403.CrossRefGoogle Scholar
Moffatt, H. & Ricca, R.L. 1992 Helicity and the Călugăreanu invariant. Proc. R. Soc. Lond. A 439, 411–429.Google Scholar
Moffatt, H.K. 1990 The energy spectrum of knots and links. Nature 347, 367–369.CrossRefGoogle Scholar
Moffatt, H.K. & Tsinoher, A. 1992 Hellicity in laminar and turbulent flow. Annu. Rev. Fluid Mech. 24, 281–312.CrossRefGoogle Scholar
Oberti, C. & Ricca, R.L. 2018 Energy and helicity of magnetic torus knots and braids. Fluid Dyn. Res. 50, 011413.CrossRefGoogle Scholar
Orlandini, E. & Whittington, S.G. 2007 Statistical topology of closed curves: some applications in polymer physics. Rev. Mod. Phys. 79, 611–642.CrossRefGoogle Scholar
Panagiotou, E. 2015 The linking number in systems with periodic boundary conditions. J. Comput. Phys. 300, 533–573.CrossRefGoogle Scholar
Parker, E.N. 1978 The mutual attraction of magnetic knots. Astrophys. J. 222, 357–364.CrossRefGoogle Scholar
Patil, V.P., Sandt, J.D., Kolle, M. & Dunkel, J. 2020 Topological mechanics of knots and tangles. Science 367, 71–75.CrossRefGoogle ScholarPubMed
Pontin, D.I. 2011 Three-dimensional magnetic reconnection regimes: a review. Adv. Space Res. 47, 1508–1522.CrossRefGoogle Scholar
Priest, E. & Forbes, T. 2000 Magnetic Reconnection: MHD Theory and Applications. Cambridge University Press.CrossRefGoogle Scholar
Priest, E.R. & Longcope, D.W. 2020 The creation of twist by reconnection of flux tubes. Sol. Phys. 295, 48.CrossRefGoogle Scholar
Raymer, D.M. & Smith, D.E. 2007 Spontaneous knotting of an agitated string. Proc. Natl Acad. Sci. USA 104, 16432–16437.CrossRefGoogle ScholarPubMed
Reidemeister, K. 1927 Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. Springer.Google Scholar
Ricca, R.L. 2013 New energy and helicity bounds for knotted and braided magnetic fields. Geophys. Astrophys. Fluid Dyn. 107, 385–402.CrossRefGoogle Scholar
Scheeler, M.W., van Rees, W.M., Kedia, H., Kleckner, D. & Irvine, W.T.M. 2017 Complete measurement of helicity and its dynamics in vortex tube. Science 357, 487–491.CrossRefGoogle Scholar
Shimokawa, K., Ishihara, K., Grainge, I., Sherratt, D.J. & Vazquez, M. 2013 FtsK-dependent XerCD-dif recombination unlinks replication catenanes in a stepwise manner. Proc. Natl Acad. Sci. USA 110, 20906–20911.CrossRefGoogle Scholar
Smiet, C.B., Candelaresi, S., Thompson, A., Swearngin, J., Dalhuisen, J.W. & Bouwmeester, D. 2015 Self-organizing knotted magnetic structures in plasma. Phys. Rev. Lett. 115, 095001.CrossRefGoogle ScholarPubMed
Smiet, C.B., Thompson, A., Bouwmeester, P. & Bouwmeester, D. 2017 Magnetic surface topology in decaying plasma knots. New J. Phys. 19, 023046.CrossRefGoogle Scholar
Stolz, R., Yoshida, M., Brasher, R., Flanner, M., Ishihara, K., Sherratt, D.J., Shimokawa, K. & Vazquez, M. 2017 Pathways of DNA unlinking: a story of stepwise simplification. Sci. Rep. 7, 12420.CrossRefGoogle ScholarPubMed
Taylor, A.J. & other SPOCK contributors 2017 pyknotid knot identification toolkit v0.5.4. https://github.com/SPOCKnots/pyknotid, accessed 25 June 2020.Google Scholar
Taylor, J.B. 1974 Relaxation of toroidal plasma and generation of reverse magnetic fields. Phys. Rev. Lett. 33, 1139–1141.CrossRefGoogle Scholar
Titov, V.S. & Démoulin, P. 1999 Basic topology of twisted magnetic configurations in solar flares. Astron. Astrophys. 351, 707–720.Google Scholar
Tkalec, U., Ravnik, M., Čopar, S., Žumer, S. & Muševič, I. 2011 Reconfigurable knots and links in chiral nematic colloids. Science 333, 62–65.CrossRefGoogle ScholarPubMed
Wang, R., Lu, Q., Nakamura, R., Huang, C., Du, A., Guo, F., Teh, W., Wu, M., Lu, S. & Wang, S. 2016 Coalescence of magnetic flux ropes in the ion diffusion region of magnetic reconnection. Nat. Phys. 12, 263–267.CrossRefGoogle Scholar
Woltjer, L. 1958 A theorem on force-free magnetic fields. Proc. Natl Acad. Sci. USA 44, 489–491.CrossRefGoogle ScholarPubMed
Xiao, C., Wang, X., Pu, Z., Ma, Z., Zhao, H., Zhou, G., Wang, J. & Liu, Z. 2007 Recent studies in satellite observations of three-dimensional magnetic reconnection. Sci. China Ser. E 50, 380–384.CrossRefGoogle Scholar
Xiong, S. & Yang, Y. 2017 The boundary-constraint method for constructing vortex-surface fields. J. Comput. Phys. 339, 31–45.CrossRefGoogle Scholar
Xiong, S. & Yang, Y. 2019 a Construction of knotted vortex tubes with the writhe-dependent helicity. Phys. Fluids 31, 047101.CrossRefGoogle Scholar
Xiong, S. & Yang, Y. 2019 b Identifying the tangle of vortex tubes in homogeneous isotropic turbulence. J. Fluid Mech. 874, 952–978.CrossRefGoogle Scholar
Xiong, S. & Yang, Y. 2020 Effects of twist on the evolution of knotted magnetic flux tubes. J. Fluid Mech. 895, A28.CrossRefGoogle Scholar
Xue, Z., et al. 2016 Observing the release of twist by magnetic reconnection in a solar filament eruption. Nat. Commun. 7, 11837.CrossRefGoogle Scholar
Yang, Y. & Pullin, D.I. 2010 On Lagrangian and vortex-surface fields for flows with Taylor–Green and Kida–Pelz initial conditions. J. Fluid Mech. 661, 446–481.CrossRefGoogle Scholar
Yang, Y. & Pullin, D.I. 2011 Evolution of vortex-surface fields in viscous Taylor–Green and Kida–Pelz flows. J. Fluid Mech. 685, 146–164.CrossRefGoogle Scholar
Yao, J. & Hussain, F. 2020 A physical model of turbulence cascade via vortex reconnection sequence and avalanche. J. Fluid Mech. 883, A53.CrossRefGoogle Scholar
Zhao, Y., Yang, Y. & Chen, S. 2016 Vortex reconnection in the late transition in channel flow. J. Fluid Mech. 802, R4.CrossRefGoogle Scholar