Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T04:00:50.224Z Has data issue: false hasContentIssue false
  • English
  • Français

Logarithmic temperature profiles in the bulk of turbulent Rayleigh–Bénard convection for a Prandtl number of 12.3

Published online by Cambridge University Press:  14 October 2014

Ping Wei  and
Guenter Ahlers
Ping Wei
Affiliation:
Department of Physics, University of California, Santa Barbara, CA 93106, USA
Guenter Ahlers*
Affiliation:
Department of Physics, University of California, Santa Barbara, CA 93106, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

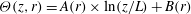We report measurements of logarithmic temperature profiles $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\varTheta (z,r) = A(r)\times \ln (z/L) + B(r)$ in the bulk of turbulent Rayleigh–Bénard convection (here 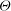$\varTheta $ is a scaled and time-averaged local temperature in the fluid, $ z$ is the vertical and $r$ the radial position, and 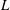$L$ is the sample height). Two samples had aspect ratios 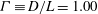$\varGamma \equiv D/L = 1.00$ and 0.50 (where 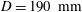$D=190\ \mathrm{mm}$ is the diameter). The fluid was a fluorocarbon with a Prandtl number of 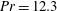$\mathit{Pr} = 12.3$. The measurements covered the Rayleigh-number range 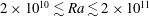$2\times 10^{10} \lesssim \mathit{Ra} \lesssim 2\times 10^{11}$ for 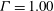$\varGamma = 1.00$ and 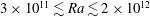$3\times 10^{11} \lesssim \mathit{Ra} \lesssim 2\times 10^{12}$ for 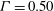$\varGamma = 0.50$. In contradistinction to what had been found for 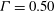$\varGamma = 0.50$ and 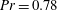$\mathit{Pr} = 0.78$ by Ahlers et al. (Phys. Rev. Lett., vol. 109, 2012, art. 114501; J. Fluid Mech., 2014, in press), the measurements revealed no 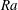$\mathit{Ra}$ dependence of the amplitude 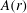$A(r)$ of the logarithmic term. Within the experimental resolution, the amplitude was also found to be independent of 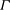$\varGamma $. It varied with $r$ in a manner consistent with the function 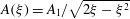$A(\xi ) = A_1/\sqrt{2\xi - \xi ^2}$, where 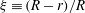$\xi \equiv (R-r)/R$ with 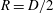$R=D/2$ and 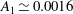$A_1 \simeq 0.0016$. The results for 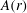$A(r)$ are smaller than those obtained from experiments and direct numerical simulations (Ahlers et al., Phys. Rev. Lett., vol. 109, 2012, art. 114501) at similar values of 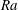$\mathit{Ra}$ for 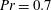$\mathit{Pr} = 0.7$ and 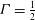$\varGamma = \frac{1}{2}$ by a factor that depended slightly upon 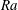$\mathit{Ra}$ but was close to 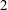$2$.

JFM classification

Convection: Convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , pp. 809 - 830
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G. 2000 Effect of sidewall conductance on heat-transport measurements for turbulent Rayleigh–Bénard convection. Phys. Rev. E 63, R015303.CrossRefGoogle ScholarPubMed
Ahlers, G. 2009 Turbulent convection. Physics 2, 74, 1–7.Google Scholar
Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Ahlers, G., Bodenschatz, E. & He, X. 2014 Logarithmic temperature profiles of turbulent Rayleigh–Bénard convection in the classical and ultimate state for a Prandtl number of 0.8. J. Fluid Mech. 758, 436–467.Google Scholar
Ahlers, G., Brown, E., Fontenele Araujo, F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck-Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–538.Google Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.CrossRefGoogle Scholar
Boussinesq, J. 1903 Theorie Analytique de la Chaleur, vol. 2. Gauthier-Villars.Google Scholar
Breuer, M., Wessling, S., Schmalzl, J. & Hansen, U. 2004 Effect of inertia in Rayleigh–Bénard convection. Phys. Rev. E 69, 026302.CrossRefGoogle ScholarPubMed
Brown, E. & Ahlers, G. 2007a Large-scale circulation model of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 134501.Google Scholar
Brown, E. & Ahlers, G. 2007b Temperature gradients, and search for non-Boussinesq effects, in the interior of turbulent Rayleigh–Bénard convection. Europhys. Lett. 80, 14001.Google Scholar
Brown, E. & Ahlers, G. 2008 A model of diffusion in a potential well for the dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20, 075101.Google Scholar
Brown, E., Nikolaenko, A., Funfschilling, D. & Ahlers, G. 2005 Heat transport in turbulent Rayleigh–Bénard convection: effect of finite top- and bottom-plate conductivity. Phys. Fluids 17, 075108.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.CrossRefGoogle ScholarPubMed
Crowder, G., Taylor, Z., Reed, T. & Young, J. 1967 Vapor pressures and triple point temperatures of several pure fluorocarbons. J. Chem. Engng Data 12, 481–485.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying view. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2012 Logarithmic temperature profiles in the ultimate regime of thermal convection. Phys. Fluids 24, 125103.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2013 Comment on “Effect of boundary layers asymmetry on heat transfer efficiency in turbulent Rayleigh–Bénard convection at very high Rayleigh numbers”. Phys. Rev. Lett. 110, 199401.Google Scholar
Hogg, J. & Ahlers, G. 2013 Reynolds-number measurements for low-Prandtl-number turbulent convection of large aspect-ratio samples. J. Fluid Mech. 725, 664–680.CrossRefGoogle Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.Google Scholar
von Kármán, T. 1930 Mechanische Ähnlichkeit und Turbulenz. Nachr. Ges. Wiss. Göttingen, Math.-Phys. Kl. 58–76, 322–336.Google Scholar
Lam, S., Shang, X. D., Zhou, S. Q. & Xia, K.-Q. 2002 Prandtl-number dependence of the viscous boundary layer and the Reynolds-number in Rayleigh–Bénard convection. Phys. Rev. E 65, 066306.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Lui, S. L. & Xia, K.-Q. 1998 Spatial structure of the thermal boundary layer in turbulent convection. Phys. Rev. E 57, 5494–5503.Google Scholar
Malkus, M. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
Millikan, C. 1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the Fifth International Congress for Applied Mechanics, pp. 386–392. Wiley.Google Scholar
Nikolaenko, A., Brown, E., Funfschilling, D. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells with aspect ratio one and less. J. Fluid Mech. 523, 251–260.Google Scholar
Oberbeck, A. 1879 Über die Wärmeleitung der Flüssigkeiten bei Berücksichtigung der Strömungen infolge von Temperaturdifferenzen. Ann. Phys. Chem. 7, 271–292.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prandtl, L. 1925 Bericht über Untersuchungen zur ausgebildeten Turbulenz. Z. Angew. Math. Mech. 5, 136–139.Google Scholar
Prandtl, L. 1932 Zur turbulenten Strömung in Rohren und längs Platten. Ergeb. Aerodyn. Versuch, Göttingen IV, 18–29.Google Scholar
Priestley, C. H. B. 1954 Convection from a large horizontal surface. Austral. J. Phys. 7, 176–201.Google Scholar
Priestley, C. H. B. 1959 Turbulent Transfer in the Lower Atmosphere. University of Chicago Press.Google Scholar
du Puits, R., Resagk, C. & Thess, A. 2009 Structure of viscous boundary layers in turbulent Rayleigh–Bénard convection. Phys. Rev. E 80, 036318.Google Scholar
Qiu, X. L. & Xia, K.-Q. 1998a Spatial structure of the viscous boundary layer in turbulent convection. Phys. Rev. E 58, 5816–5820.Google Scholar
Qiu, X. L. & Xia, K.-Q. 1998b Viscous boundary layers at the sidewall of a convection cell. Phys. Rev. E 58, 486–491.Google Scholar
Roche, P., Castaing, B., Chabaud, B., Hebral, B. & Sommeria, J. 2001 Side wall effects in Rayleigh Bénard experiments. Eur. Phys. J. 24, 405–408.Google Scholar
Schmalzl, J., Breuer, M. & Hansen, U. 2002 The influence of the Prandtl number on the style of vigorous thermal convection. Geophys. Astrophys. Fluid Dyn. 96, 381–403.Google Scholar
She, Z.-S., Chen, X., Chen, J., Zou, H.-Y., Bao, Y. & Hussain, F.2014 Prediction of temperature distribution in turbulent Rayleigh–Bénard convection. arXiv:1401.2138.Google Scholar
Shishkina, O., Stevens, R., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Spiegel, E. A. 1971 Convection in stars. Annu. Rev. Astron. Astrophys. 9, 323–352.Google Scholar
Stevens, J., van der Poel, E., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.Google Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.Google Scholar
Sun, C., Ren, L.-Y., Song, H. & Xia, K.-Q. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells of widely varying aspect ratios. J. Fluid Mech. 542, 165–174.Google Scholar
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulence convection in water. Phys. Rev. E 47, R2253–R2256.Google Scholar
Urban, P., Hanzelka, P., Kralik, T., Musilova, V., Srnka, A. & Skrbek, L. 2012 Effect of boundary layers asymmetry on heat transfer efficiency in turbulent Rayleigh–Bénard convection at very high Rayleigh numbers. Phys. Rev. Lett. 109, 154301.Google Scholar
Xu, X., Bajaj, K. M. S. & Ahlers, G. 2000 Heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 84, 4357–4360.Google Scholar
Zhong, J.-Q. & Ahlers, G. 2010 Heat transport and the large-scale circulation in rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 665, 300–333.Google Scholar