Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T22:51:51.421Z Has data issue: false hasContentIssue false
  • English
  • Français

A localized turbulent mixing layer in a uniformly stratified environment

Published online by Cambridge University Press:  18 June 2018

Tomoaki Watanabe Open the ORCID record for Tomoaki Watanabe [Opens in a new window] ,
James J. Riley ,
Koji Nagata Open the ORCID record for Koji Nagata [Opens in a new window] ,
Ryo Onishi  and
Keigo Matsuda
Tomoaki Watanabe*
Affiliation:
Department of Aerospace Engineering, Nagoya University, Nagoya 464-8603, Japan
James J. Riley
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle 98195, USA
Koji Nagata
Affiliation:
Department of Aerospace Engineering, Nagoya University, Nagoya 464-8603, Japan
Ryo Onishi
Affiliation:
Earth Simulator Center, Japan Agency for Marine-Earth Science and Technology, Yokohama 236-0001, Japan
Keigo Matsuda
Affiliation:
Earth Simulator Center, Japan Agency for Marine-Earth Science and Technology, Yokohama 236-0001, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Localized turbulence bounded by non-turbulent flow in a uniformly stratified environment is studied with direct numerical simulations of stably stratified shear layers. Of particular interest is the turbulent/non-turbulent interfacial (TNTI) layer, which is detected by identifying the turbulent region in terms of its potential vorticity. Fluid near the outer edge of the turbulent region gains potential vorticity and becomes turbulent by diffusion arising from both viscous and molecular effects. The flow properties near the TNTI layer change depending on the buoyancy Reynolds number near the interface, 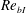$Re_{bI}$. The TNTI layer thickness is approximately 13 times the Kolmogorov length scale for large 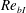$Re_{bI}$ (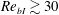$Re_{bI}\gtrsim 30$), consistent with non-stratified flows, whereas it is almost equal to the vertical length scale of the stratified flow, 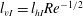$l_{vI}=l_{hI}Re^{-1/2}$ (here 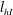$l_{hI}$ is the horizontal length scale near the TNTI layer, and 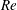$Re$ is the Reynolds number), in the low-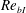$Re_{bI}$ regime (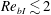$Re_{bI}\lesssim 2$). Turbulent fluid is vertically transported towards the TNTI layer when 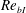$Re_{bI}$ is large, sustaining the thin TNTI layer with large buoyancy frequency and mean shear. This sharpening effect is weakened as 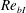$Re_{bI}$ decreases and eventually becomes negligible for very low 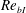$Re_{bI}$. Overturning motions occur near the TNTI layer for large 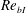$Re_{bI}$. The dependence on buoyancy Reynolds number is related to the value of 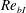$Re_{bI}$ near the TNTI layer, which is smaller than the value deep inside the turbulent core region. An imprint of the internal gravity waves propagating in the non-turbulent region is found for vorticity within the TNTI layer, inferring an interaction between turbulence and internal gravity waves. The wave energy flux causes a net loss of the kinetic energy in the turbulent core region bounded to the TNTI layer, and the amount of kinetic energy extracted from the turbulent region by internal gravity waves is comparable to the amount dissipated in the turbulent region.

JFM classification

Geophysical and Geological Flows: Internal waves Turbulent Flows: Shear layer turbulence Turbulent Flows: Stratified turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 245 - 276
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdilghanie, A. M. & Diamessis, P. J. 2013 The internal gravity wave field emitted by a stably stratified turbulent wake. J. Fluid Mech. 720, 104–139.Google Scholar
Attili, A., Cristancho, J. C. & Bisetti, F. 2014 Statistics of the turbulent/non-turbulent interface in a spatially developing mixing layer. J. Turbul. 15 (9), 555–568.Google Scholar
Barry, M. E., Ivey, G. N., Winters, K. B. & Imberger, J. 2001 Measurements of diapycnal diffusivities in stratified fluids. J. Fluid Mech. 442, 267–291.Google Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.Google Scholar
Brucker, K. A. & Sarkar, S. 2010 A comparative study of self-propelled and towed wakes in a stratified fluid. J. Fluid Mech. 652, 373–404.Google Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. No. TN-1244.Google Scholar
Diamessis, P. J., Spedding, G. R. & Domaradzki, J. A. 2011 Similarity scaling and vorticity structure in high-Reynolds-number stably stratified turbulent wakes. J. Fluid Mech. 671, 52–95.Google Scholar
Duck, T. J. & Whiteway, J. A. 2005 The spectrum of waves and turbulence at the tropopause. Geophys. Res. Lett. 32, L07801.Google Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6, 423–448.Google Scholar
Finnigan, J. J., Einaudi, F. & Fua, D. 1984 The interaction between an internal gravity wave and turbulence in the stably-stratified nocturnal boundary layer. J. Atmos. Sci. 41 (16), 2409–2436.Google Scholar
Fritts, D. C. & Alexander, M. J. 2003 Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 41, 1003.Google Scholar
Godoy-Diana, R., Chomaz, J.-M. & Billant, P. 2004 Vertical length scale selection for pancake vortices in strongly stratified viscous fluids. J. Fluid Mech. 504, 229–238.Google Scholar
Hazel, P. 1972 Numerical studies of the stability of inviscid stratified shear flows. J. Fluid Mech. 51, 39–61.Google Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106 (13), 134503.Google Scholar
Hopfinger, E. J., Flor, J. B., Chomaz, J. M. & Bonneton, P. 1991 Internal waves generated by a moving sphere and its wake in a stratified fluid. Exp. Fluids 11 (4), 255–261.Google Scholar
Hunt, J. C. R., Moustaoui, M. & Mahalov, A. 2015 The eddy, wave, and interface structure of turbulent shear layers below/above stably stratified regions. J. Geophys. Res. 120 (18), 9237–9257.Google Scholar
Jahanbakhshi, R., Vaghefi, N. S. & Madnia, C. K. 2015 Baroclinic vorticity generation near the turbulent/non-turbulent interface in a compressible shear layer. Phys. Fluids 27 (10), 105105.Google Scholar
Jimenez, J. & Wray, A. A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.Google Scholar
Kempf, A., Klein, M. & Janicka, J. 2005 Efficient generation of initial- and inflow-conditions for transient turbulent flows in arbitrary geometries. Flow Turbul. Combust. 74 (1), 67–84.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2015 The turbulent/non-turbulent interface in an inclined dense gravity current. J. Fluid Mech. 765, 303–324.Google Scholar
Krug, D., Holzner, M., Marusic, I. & van Reeuwijk, M. 2017 Fractal scaling of the turbulence interface in gravity currents. J. Fluid Mech. 820, R3.Google Scholar
de Lavergne, C., Madec, G., Le Sommer, J., Nurser, A. J. G. & Naveira Garabato, A. C. 2016 The impact of a variable mixing efficiency on the abyssal overturning. J. Phys. Oceanogr. 46 (2), 663–681.Google Scholar
Linden, P. F. 1975 The deepening of a mixed layer in a stratified fluid. J. Fluid Mech. 71, 385–405.Google Scholar
Maffioli, A., Davidson, P. A., Dalziel, S. B. & Swaminathan, N. 2014 The evolution of a stratified turbulent cloud. J. Fluid Mech. 739, 229–253.Google Scholar
Mahrt, L. 1999 Stratified atmospheric boundary layers. Boundary-Layer Meteorol. 90 (3), 375–396.Google Scholar
Morinishi, Y., Lund, T. S., Vasilyev, O. V. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143 (1), 90–124.Google Scholar
Moum, J. N., Hebert, D., Paulson, C. A. & Caldwell, D. R. 1992 Turbulence and internal waves at the equator. Part I: statistics from towed thermistors and a microstructure profiler. J. Phys. Oceanogr. 22 (11), 1330–1345.Google Scholar
Nagarajan, S., Lele, S. K. & Ferziger, J. H. 2003 A robust high-order compact method for large eddy simulation. J. Comput. Phys. 191 (2), 392–419.Google Scholar
Nash, J. D., Alford, M. H. & Kunze, E. 2005 Estimating internal wave energy fluxes in the ocean. J. Atmos. Ocean. Technol. 22 (10), 1551–1570.Google Scholar
Pham, H. T. & Sarkar, S. 2010 Transport and mixing of density in a continuously stratified shear layer. J. Turbul. (11), N24.Google Scholar
Pham, H. T., Sarkar, S. & Brucker, K. A. 2009 Dynamics of a stratified shear layer above a region of uniform stratification. J. Fluid Mech. 630, 191–223.Google Scholar
Philip, J., Meneveau, C., de Silva, C. M. & Marusic, I. 2014 Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers. Phys. Fluids 26 (1), 015105.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Portwood, G. D., de Bruyn Kops, S. M., Taylor, J. R., Salehipour, H. & Caulfield, C. P. 2016 Robust identification of dynamically distinct regions in stratified turbulence. J. Fluid Mech. 807, R2.Google Scholar
Poulos, G. S., Blumen, W., Fritts, D. C., Lundquist, J. K., Sun, J., Burns, S. P., Nappo, C., Banta, R., Newsom, R., Cuxart, J., Terradellas, E., Balsley, B. & Jensen, M. 2002 CASES-99: A comprehensive investigation of the stable nocturnal boundary layer. Bull. Am. Meteorol. Soc. 83 (4), 555–581.Google Scholar
van Reeuwijk, M. & Holzner, M. 2014 The turbulence boundary of a temporal jet. J. Fluid Mech. 739, 254–275.Google Scholar
Riley, J. J. & Lelong, M.-P. 2000 Fluid motions in the presence of strong stable stratification. Annu. Rev. Fluid Mech. 32 (1), 613–657.Google Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
da Silva, C. B., Dos Reis, R. J. N. & Pereira, J. C. F. 2011 The intense vorticity structures near the turbulent/non-turbulent interface in a jet. J. Fluid Mech. 685, 165–190.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent–nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111 (4), 044501.Google Scholar
Smyth, W. D. & Moum, J. N. 2002 Shear instability and gravity wave saturation in an asymmetrically stratified jet. Dyn. Atmos. Oceans 35 (3), 265–294.Google Scholar
Spedding, G. R. 2002 Vertical structure in stratified wakes with high initial Froude number. J. Fluid Mech. 454, 71–112.Google Scholar
Spedding, G. R., Browand, F. K. & Fincham, A. M. 1996 Turbulence, similarity scaling and vortex geometry in the wake of a towed sphere in a stably stratified fluid. J. Fluid Mech. 314, 53–103.Google Scholar
de Stadler, M. B., Sarkar, S. & Brucker, K. A. 2010 Effect of the Prandtl number on a stratified turbulent wake. Phys. Fluids 22 (9), 095102.Google Scholar
Strang, E. J. & Fernando, H. J. S. 2001 Entrainment and mixing in stratified shear flows. J. Fluid Mech. 428, 349–386.Google Scholar
Sutherland, B. R. 1996 Dynamic excitation of internal gravity waves in the equatorial oceans. J. Phys. Oceanogr. 26 (11), 2398–2419.Google Scholar
Suzuki, H., Nagata, K., Sakai, Y., Hayase, T., Hasegawa, Y. & Ushijima, T. 2013 An attempt to improve accuracy of higher-order statistics and spectra in direct numerical simulation of incompressible wall turbulence by using the compact schemes for viscous terms. Intl J. Numer. Meth. Fluids 73 (6), 509–522.Google Scholar
Tanahashi, M., Iwase, S. & Miyauchi, T. 2001 Appearance and alignment with strain rate of coherent fine scale eddies in turbulent mixing layer. J. Turbul. 2 (6), 1–18.Google Scholar
Taveira, R. R., Diogo, J. S., Lopes, D. C. & da Silva, C. B. 2013 Lagrangian statistics across the turbulent–nonturbulent interface in a turbulent plane jet. Phys. Rev. E 88 (4), 043001.Google Scholar
Taveira, R. R. & da Silva, C. B. 2014 Characteristics of the viscous superlayer in shear free turbulence and in planar turbulent jets. Phys. Fluids 26 (2), 021702.Google Scholar
Taylor, J. R. & Sarkar, S. 2007 Internal gravity waves generated by a turbulent bottom Ekman layer. J. Fluid Mech. 590, 331–354.Google Scholar
Thorpe, S. A. 1978 The near-surface ocean mixing layer in stable heating conditions. J. Geophys. Res. 83 (C6), 2875–2885.Google Scholar
Tse, K.-L., Mahalov, A., Nicolaenko, B. & Fernando, H. J. S. 2003 Quasi-equilibrium dynamics of shear-stratified turbulence in a model tropospheric jet. J. Fluid Mech. 496, 73–103.Google Scholar
Van der Vorst, H. A. 1992 Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 13 (2), 631–644.Google Scholar
Watanabe, T., Jaulino, R., Taveira, R. R., da Silva, C. B., Nagata, K. & Sakai, Y. 2017a Role of an isolated eddy near the turbulent/non-turbulent interface layer. Phys. Rev. Fluids 2 (9), 094607.Google Scholar
Watanabe, T., Nagata, K. & da Silva, C. B. 2017b Vorticity evolution near the turbulent/non-turbulent interfaces in free-shear flows. In Vortex Structures in Fluid Dynamic Problems. InTech.Google Scholar
Watanabe, T., Riley, J. J., de Bruyn Kops, S. M., Diamessis, P. J. & Zhou, Q. 2016a Turbulent/non-turbulent interfaces in wakes in stably stratified fluids. J. Fluid Mech. 797, R1.Google Scholar
Watanabe, T., Riley, J. J. & Nagata, K. 2016b Effects of stable stratification on turbulent/nonturbulent interfaces in turbulent mixing layers. Phys. Rev. Fluids 1 (4), 044301.Google Scholar
Watanabe, T., Riley, J. J. & Nagata, K. 2017c Turbulent entrainment across turbulent–nonturbulent interfaces in stably stratified mixing layers. Phys. Rev. Fluids 2 (10), 104803.Google Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2015 Turbulent mixing of passive scalar near turbulent and non-turbulent interface in mixing layers. Phys. Fluids 27 (8), 085109.Google Scholar
Watanabe, T., Zhang, X. & Nagata, K. 2018 Turbulent/non-turbulent interfaces detected in DNS of incompressible turbulent boundary layers. Phys. Fluids 30 (3), 035102.Google Scholar
Westerweel, J., Hofmann, T., Fukushima, C. & Hunt, J. C. R. 2002 The turbulent/non-turbulent interface at the outer boundary of a self-similar turbulent jet. Exp. Fluids 33 (6), 873–878.Google Scholar