Published online by Cambridge University Press: 08 October 2015
Direct numerical simulations of transitional flow in a rectangular duct of cross-sectional aspect ratio 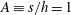 $A\equiv s/h=1$–9 (
$A\equiv s/h=1$–9 ( $s$ and
$s$ and 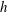 $h$ being the duct half-span and half-height, respectively) have been performed in the Reynolds number range
$h$ being the duct half-span and half-height, respectively) have been performed in the Reynolds number range 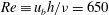 $\mathit{Re}\equiv u_{b}h/{\it\nu}=650$–1500 (
$\mathit{Re}\equiv u_{b}h/{\it\nu}=650$–1500 (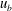 $u_{b}$ and
$u_{b}$ and  ${\it\nu}$ being the bulk velocity and the kinematic viscosity, respectively) in order to investigate the dependence on the aspect ratio of spatially localized turbulence structures. It was observed that the lowest Reynolds number
${\it\nu}$ being the bulk velocity and the kinematic viscosity, respectively) in order to investigate the dependence on the aspect ratio of spatially localized turbulence structures. It was observed that the lowest Reynolds number 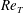 $\mathit{Re}_{T}$, estimated in a specific way, for localized (transiently sustaining) turbulence decreases monotonically from
$\mathit{Re}_{T}$, estimated in a specific way, for localized (transiently sustaining) turbulence decreases monotonically from 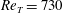 $\mathit{Re}_{T}=730$ for
$\mathit{Re}_{T}=730$ for 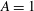 $A=1$ (square duct) with increasing aspect ratio, and for
$A=1$ (square duct) with increasing aspect ratio, and for 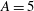 $A=5$ it nearly attains a minimal value
$A=5$ it nearly attains a minimal value 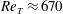 $\mathit{Re}_{T}\approx 670$ that is consistent with the onset Reynolds number of turbulent spots in a plane channel (
$\mathit{Re}_{T}\approx 670$ that is consistent with the onset Reynolds number of turbulent spots in a plane channel (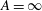 $A=\infty$). Turbulent states consist of localized structures that undergo a fundamental change around
$A=\infty$). Turbulent states consist of localized structures that undergo a fundamental change around 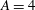 $A=4$. At
$A=4$. At 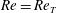 $\mathit{Re}=\mathit{Re}_{T}$ turbulence for
$\mathit{Re}=\mathit{Re}_{T}$ turbulence for 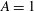 $A=1$–
$A=1$–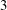 $3$ is streamwise-localized similar to turbulent puffs in pipe flow, while for
$3$ is streamwise-localized similar to turbulent puffs in pipe flow, while for 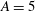 $A=5$–9 turbulence at
$A=5$–9 turbulence at 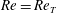 $\mathit{Re}=\mathit{Re}_{T}$ is also localized in the spanwise direction, similar to turbulent spots in plane channel flow. This structural change in turbulent states at
$\mathit{Re}=\mathit{Re}_{T}$ is also localized in the spanwise direction, similar to turbulent spots in plane channel flow. This structural change in turbulent states at 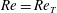 $\mathit{Re}=\mathit{Re}_{T}$ is attributed to the exclusion of turbulence from the vicinity of the duct sidewalls in the case of a wide duct with
$\mathit{Re}=\mathit{Re}_{T}$ is attributed to the exclusion of turbulence from the vicinity of the duct sidewalls in the case of a wide duct with 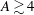 $A\gtrsim 4$: here the friction length on the sidewalls is so long that the size (around 100 times the friction length) of a self-sustaining minimal flow unit of streamwise vortices and streaks is larger than the duct height and, therefore, it cannot be accommodated.
$A\gtrsim 4$: here the friction length on the sidewalls is so long that the size (around 100 times the friction length) of a self-sustaining minimal flow unit of streamwise vortices and streaks is larger than the duct height and, therefore, it cannot be accommodated.