Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T21:40:52.272Z Has data issue: false hasContentIssue false
  • English
  • Français

Local boundary layer scales in turbulent Rayleigh–Bénard convection

Published online by Cambridge University Press:  08 October 2014

Janet D. Scheel  and
Jörg Schumacher
Janet D. Scheel*
Affiliation:
Department of Physics, Occidental College, 1600 Campus Road, M21, Los Angeles, CA 90041, USA
Jörg Schumacher
Affiliation:
Institut für Thermo- und Fluiddynamik, Postfach 100565, Technische Universität Ilmenau, D-98684 Ilmenau, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We compute fully local boundary layer scales in three-dimensional turbulent Rayleigh–Bénard convection. These scales are directly connected to the highly intermittent fluctuations of the fluxes of momentum and heat at the isothermal top and bottom walls and are statistically distributed around the corresponding mean thickness scales. The local boundary layer scales also reflect the strong spatial inhomogeneities of both boundary layers due to the large-scale, but complex and intermittent, circulation that builds up in closed convection cells. Similar to turbulent boundary layers, we define inner scales based on local shear stress that can be consistently extended to the classical viscous scales in bulk turbulence, e.g. the Kolmogorov scale, and outer scales based on slopes at the wall. We discuss the consequences of our generalization, in particular the scaling of our inner and outer boundary layer thicknesses and the resulting shear Reynolds number with respect to the Rayleigh number. The mean outer thickness scale for the temperature field is close to the standard definition of a thermal boundary layer thickness. In the case of the velocity field, under certain conditions the outer scale follows a scaling similar to that of the Prandtl–Blasius type definition with respect to the Rayleigh number, but differs quantitatively. The friction coefficient 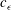$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}c_{\epsilon }$ scaling is found to fall right between the laminar and turbulent limits, which indicates that the boundary layer exhibits transitional behaviour. Additionally, we conduct an analysis of the recently suggested dissipation layer thickness scales versus the Rayleigh number and find a transition in the scaling. All our investigations are based on highly accurate spectral element simulations that reproduce gradients and their fluctuations reliably. The study is done for a Prandtl number of 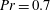$\mathit{Pr}=0.7$ and for Rayleigh numbers that extend over almost five orders of magnitude, 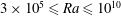$3\times 10^5\le \mathit{Ra} \le 10^{10}$, in cells with an aspect ratio of one. We also performed one study with an aspect ratio equal to three in the case of 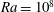$\mathit{Ra}=10^8$. For both aspect ratios, we find that the scale distributions depend on the position at the plates where the analysis is conducted.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , pp. 344 - 373
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.Google Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1994 Temperature and velocity boundary layers in turbulent convection. Phys. Rev. E 50, 269–279.Google Scholar
Blasius, H. 1908 Grenzschichten in Flüssigkeiten mit kleiner Reibung. Z. Math. Phys. 56, 1–37.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. J. Phys. 35, 58.Google Scholar
Chong, M. S., Monty, J. P., Chin, C. & Marusic, I. 2012 The topology of skin friction and surface vorticity fields in wall-bounded flows. J. Turbul. 13 (6), 1–10.Google Scholar
Deville, M. O., Fischer, P. F. & Mund, E. H. 2002 High-order Methods for Incompressible Fluid Flow. Cambridge University Press.Google Scholar
Fischer, P. F. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133, 84–101.Google Scholar
Grosse, S. & Schröder, W. 2009 Wall-shear stress patterns of coherent structures in turbulent duct flow. J. Fluid Mech. 633, 147–158.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grötzbach, G. 1983 Spatial resolution requirements for direct numerical simulation of the Rayleigh–Bénard convection. J. Comput. Phys. 49, 241–269.Google Scholar
Hamlington, P. E., Krasnov, D., Boeck, T. & Schumacher, J. 2012 Local dissipation scales and energy dissipation-rate moments in channel flow. J. Fluid Mech. 701, 419–429.Google Scholar
Hartlep, T., Tilgner, A. & Busse, F. H. 2005 Transition to turbulent convection in a fluid layer heated from below at moderate aspect ratio. J. Fluid Mech. 554, 309–322.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502 (4 pages).Google Scholar
Kaiser, R. & du Puits, R. 2014 Local wall heat flux in confined thermal convection. Intl J. Heat Mass Transfer 73, 752–760.Google Scholar
Li, L., Shi, N., du Puits, R., Resagk, C., Schumacher, J. & Thess, A. 2012 Boundary layer analysis in turbulent Rayleigh–Bénard convection in air: experiment versus simulation. Phys. Rev. E 86, 026315 (12 pages).Google Scholar
Lui, S.-L. & Xia, K.-Q. 1998 Spatial structure of the thermal boundary layer in turbulent convection. Phys. Rev. E 57, 5494–5503.Google Scholar
Petschel, K., Stellmach, S., Wilczek, M., Lülff, J. & Hansen, U. 2013 Dissipation layers in Rayleigh–Bénard convection: a unifying view. Phys. Rev. Lett. 110, 114502 (4 pages).Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prandtl, L. 1905 Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Proceedings of the III. International Mathematicians Congress, Heidelberg, 1904, pp. 484–491. B. G. Teubner.Google Scholar
du Puits, R., Li, L., Resagk, C., Thess, A. & Willert, C. 2014 Turbulent boundary layer in high Rayleigh number convection in air. Phys. Rev. Lett. 112, 124301 (4 pages).Google Scholar
du Puits, R., Resagk, C. & Thess, A. 2010 Measurements of the instantaneous local heat flux in turbulent Rayeigh–Bénard convection. New J. Phys. 12, 075023 (13 pages).Google Scholar
du Puits, R., Resagk, C., Tilgner, C., Busse, F. H. & Thess, A. 2007b Structure of thermal boundary layers in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 572, 231–254.Google Scholar
Qiu, X.-L. & Xia, K.-Q. 1998 Spatial structure of the viscous boundary layer in turbulent convection. Phys. Rev. E 58, 5816–5820.Google Scholar
Scheel, J. D., Emran, M. S. & Schumacher, J. 2013 Resolving the fine-scale structure in turbulent Rayleigh–Bénard convection. New J. Phys. 15, 113063 (32 pages).Google Scholar
Scheel, J. D., Kim, E. & White, K. R. 2012 Thermal and viscous boundary layers in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 711, 281–305.Google Scholar
Schumacher, J. 2007 Sub-Kolmogorov scale fluctuations in fluid turbulence. Europhys. Lett. 80, 54001 (6 pages).Google Scholar
Schumacher, J., Scheel, J. D., Krasnov, D., Donzis, D. A., Yakhot, V. & Sreenivasan, K. R. 2014 Small-scale universality in fluid turbulence. Proc. Natl Acad. Sci. USA 111, 10961–10965.Google Scholar
Schumacher, J., Yeung, P. K. & Sreenivasan, K. R. 2005 Very fine structures in scalar mixing. J. Fluid Mech. 531, 113–122.CrossRefGoogle Scholar
Shi, N., Emran, M. S. & Schumacher, J. 2012 Boundary layer structure in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 706, 5–33.Google Scholar
Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.Google Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.Google Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2012 Thermal boundary layer profiles in turbulent Rayleigh–Bénard convection in a cylindrical sample. Phys. Rev. E 85, 027301 (5 pages).Google Scholar
Sun, C., Cheung, Y.-H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.Google Scholar
Trompert, R. & Hansen, U. 1998 Mantle convection simulations with rheologies that generate plate-like behaviour. Nature 395, 686–689.CrossRefGoogle Scholar
Urban, P., Hanzelka, P., Kralik, T., Musilova, V., Srnka, A. & Skrebk, L. 2012 Effect of boundary layers asymmetry on heat transfer efficiency in turbulent Rayleigh–Bérnard convection at very high Rayleigh numbers. Phys. Rev. Lett. 109, 154301 (4 pages).Google Scholar
van Reeuwijk, M., Jonker, H. J. J. & Hanjalić, K. 2008b Wind and boundary layers in Rayleigh–Bénard convection. II. Boundary layer character and scaling. Phys. Rev. E 77, 036312 (10 pages).Google ScholarPubMed
Verzicco, R. & Camussi, R. 1999 Prandtl number effects in convective turbulence. J. Fluid Mech. 383, 55–73.CrossRefGoogle Scholar
Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.Google Scholar
Wagner, S., Shishkina, O. & Wagner, C. 2012 Boundary layers and wind in cylindrical Rayleigh–Bénard cells. J. Fluid Mech. 697, 336–366.Google Scholar
Wei, P. & Xia, K.-Q. 2013 Viscous boundary layer properties in turbulent thermal convection in a cylindrical cell: the effect of cell tilting. J. Fluid Mech. 720, 140–168.Google Scholar
Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.Google Scholar
Zhou, Q., Sugiyama, K., Stevens, R. J. A. M., Grossmann, S., Lohse, D. & Xia, K.-Q. 2011 Horizontal structures of velocity and temperature boundary layers in two-dimensional numerical turbulent Rayleigh–Bénard convection. Phys. Fluids 23, 125104.Google Scholar
Zhou, Q. & Xia, K.-Q. 2010a Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301 (4 pages).Google Scholar
Zhou, Q. & Xia, K.-Q. 2010b Universality of local dissipation scales in buoyancy-driven turbulence. Phys. Rev. Lett. 104, 124301 (4 pages).Google Scholar