Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Buijsman, M. C.
Kanarska, Y.
and
McWilliams, J. C.
2010.
On the generation and evolution of nonlinear internal waves in the South China Sea.
Journal of Geophysical Research: Oceans,
Vol. 115,
Issue. C2,
MOLEMAKER, M. JEROEN
MCWILLIAMS, JAMES C.
and
CAPET, XAVIER
2010.
Balanced and unbalanced routes to dissipation in an equilibrated Eady flow.
Journal of Fluid Mechanics,
Vol. 654,
Issue. ,
p.
35.
Wood, Richard B.
and
McIntyre, Michael E.
2010.
A General Theorem on Angular-Momentum Changes due to Potential Vorticity Mixing and on Potential-Energy Changes due to Buoyancy Mixing.
Journal of the Atmospheric Sciences,
Vol. 67,
Issue. 4,
p.
1261.
Kang, Dujuan
and
Fringer, Oliver
2010.
On the Calculation of Available Potential Energy in Internal Wave Fields.
Journal of Physical Oceanography,
Vol. 40,
Issue. 11,
p.
2539.
Burls, N. J.
Reason, C. J. C.
Penven, P.
and
Philander, S. G.
2011.
Similarities between the tropical Atlantic seasonal cycle and ENSO: An energetics perspective.
Journal of Geophysical Research: Oceans,
Vol. 116,
Issue. C11,
Vallgren, Andreas
Deusebio, Enrico
and
Lindborg, Erik
2011.
Possible Explanation of the Atmospheric Kinetic and Potential Energy Spectra.
Physical Review Letters,
Vol. 107,
Issue. 26,
Sheen, K. L.
White, N. J.
Caulfield, C. P.
and
Hobbs, R. W.
2012.
Seismic imaging of a large horizontal vortex at abyssal depths beneath the Sub-Antarctic Front.
Nature Geoscience,
Vol. 5,
Issue. 8,
p.
542.
Seim, Knut S.
Fer, Ilker
and
Avlesen, Helge
2012.
Stratified flow over complex topography: A model study of the bottom drag and associated mixing.
Continental Shelf Research,
Vol. 34,
Issue. ,
p.
41.
Burls, N. J.
Reason, C. J. C
Penven, P.
and
Philander, S. G.
2012.
Energetics of the Tropical Atlantic Zonal Mode.
Journal of Climate,
Vol. 25,
Issue. 21,
p.
7442.
Almalkie, Saba
and
de Bruyn Kops, Stephen M.
2012.
Kinetic energy dynamics in forced, homogeneous, and axisymmetric stably stratified turbulence.
Journal of Turbulence,
Vol. 13,
Issue. ,
p.
N29.
Riley, James J.
and
Lindborg, Erik
2012.
Ten Chapters in Turbulence.
p.
269.
Tailleux, Rémi
2013.
Available potential energy density for a multicomponent Boussinesq fluid with arbitrary nonlinear equation of state.
Journal of Fluid Mechanics,
Vol. 735,
Issue. ,
p.
499.
Tailleux, Rémi
2013.
Available Potential Energy and Exergy in Stratified Fluids.
Annual Review of Fluid Mechanics,
Vol. 45,
Issue. 1,
p.
35.
Augier, Pierre
and
Lindborg, Erik
2013.
A New Formulation of the Spectral Energy Budget of the Atmosphere, with Application to Two High-Resolution General Circulation Models.
Journal of the Atmospheric Sciences,
Vol. 70,
Issue. 7,
p.
2293.
Winters, Kraig B.
and
Barkan, Roy
2013.
Available potential energy density for Boussinesq fluid flow.
Journal of Fluid Mechanics,
Vol. 714,
Issue. ,
p.
476.
Hogg, Andrew McC.
Dijkstra, Henk A.
and
Saenz, Juan A.
2013.
The Energetics of a Collapsing Meridional Overturning Circulation.
Journal of Physical Oceanography,
Vol. 43,
Issue. 7,
p.
1512.
Brune, Sebastian
and
Becker, Erich
2013.
Indications of Stratified Turbulence in a Mechanistic GCM.
Journal of the Atmospheric Sciences,
Vol. 70,
Issue. 1,
p.
231.
Barkan, Roy
Winters, Kraig B.
and
Llewellyn Smith, Stefan G.
2013.
Rotating horizontal convection.
Journal of Fluid Mechanics,
Vol. 723,
Issue. ,
p.
556.
Deusebio, Enrico
Vallgren, A.
and
Lindborg, E.
2013.
The route to dissipation in strongly stratified and rotating flows.
Journal of Fluid Mechanics,
Vol. 720,
Issue. ,
p.
66.
Scotti, Alberto
and
White, Brian
2014.
Diagnosing mixing in stratified turbulent flows with a locally defined available potential energy.
Journal of Fluid Mechanics,
Vol. 740,
Issue. ,
p.
114.
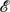 ap is defined as the difference between the gravitational potential energy of the system and the potential energy of a reference state with the lowest potential energy that can be reached by adiabatic material rearrangement;
ap is defined as the difference between the gravitational potential energy of the system and the potential energy of a reference state with the lowest potential energy that can be reached by adiabatic material rearrangement; 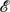 ap determines how much energy is available for conservative dynamical exchange with kinetic energy
ap determines how much energy is available for conservative dynamical exchange with kinetic energy 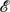 k. In this paper we introduce new techniques for computing the local available potential energy density Eap in numerical simulations that allow for a more accurate and complete analysis of the available potential energy and its dynamical balances as part of the complete energy cycle of a flow. In particular, the definition of Eap and an associated gravitation disturbance field
k. In this paper we introduce new techniques for computing the local available potential energy density Eap in numerical simulations that allow for a more accurate and complete analysis of the available potential energy and its dynamical balances as part of the complete energy cycle of a flow. In particular, the definition of Eap and an associated gravitation disturbance field 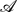 permit us to make a spectral decomposition of its dynamical balance and examine the cross-scale energy flux. Several examples illustrate the spatial structure of Eap and its evolutionary influences. The greatest attention is given to an analysis of a turbulent-equilibrium simulation Eady-like vertical-shear flow with rotation and stable stratification. In this regime Eap exhibits a vigorous forward energy cascade from the mesoscale through the submesoscale range – first in a scale range dominated by frontogenesis and positive buoyancy-flux conversion from
permit us to make a spectral decomposition of its dynamical balance and examine the cross-scale energy flux. Several examples illustrate the spatial structure of Eap and its evolutionary influences. The greatest attention is given to an analysis of a turbulent-equilibrium simulation Eady-like vertical-shear flow with rotation and stable stratification. In this regime Eap exhibits a vigorous forward energy cascade from the mesoscale through the submesoscale range – first in a scale range dominated by frontogenesis and positive buoyancy-flux conversion from 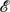 ap to
ap to 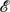 k and then, after strong frontal instability and frontogenetic arrest, in a coupled kinetic-potential energy inertial-cascade range with negative buoyancy-flux conversion – en route to fine-scale dissipation of both energy components.
k and then, after strong frontal instability and frontogenetic arrest, in a coupled kinetic-potential energy inertial-cascade range with negative buoyancy-flux conversion – en route to fine-scale dissipation of both energy components.