Article contents
Linear instability and nonlinear flow states in a horizontal pipe flow under bottom heating and transverse magnetic field
Published online by Cambridge University Press: 14 December 2022
Abstract
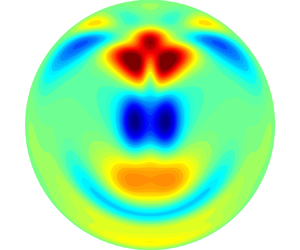
Linear stabilities of the liquid metal mixed convection in a horizontal pipe under bottom heating and transverse magnetic field are studied through linear global stability analyses. Three branches of the linear stability boundary curves are determined by the eigenvalue computation of the most unstable modes. One branch is located in the region of large Hartmann number and determined by the linear unstable mode which was first revealed by the numerical simulations of Zikanov, Listratov & Sviridov (J. Fluid Mech., vol. 720, 2013, pp. 486–516). This branch curve shows that the global unstable mode exists above a threshold of Hartmann number, which agrees with the experiment of Genin et al. (Temperature fluctuations in a heated horizontal tube affected by transverse magnetic field. In Proc. 8th PAMIR Conf. Fund. Appl. MHD, Borgo, Corsica, France, pp. 37–41, 2011). The other two branch curves determined by two different long-wave unstable modes intersect with each other in the region of small Hartmann number. The critical Grashof number on these two curves increases exponentially with the increase of the Hartmann number. Through energy budget analyses at the critical thresholds of these unstable modes, it is found that, for the unstable mode at large Hartmann numbers, buoyancy is the dominant destabilizing term which demonstrates the hypothetical explanation of Zikanov et al. (2013) who regard natural convection as a destabilization mechanism. It is further revealed that, with respect to the unstable modes on the critical stability curves of small Hartmann numbers, the dominant destabilization comes from the streamwise shear of the basic flow. Finally, within the linear unstable region, fully developed nonlinear flow states of the mixed convection are investigated by direct numerical simulations (DNS) with several sets of selected dimensionless parameters. The spatio-temporal structures of these nonlinear flow states are discussed in detail with comparison with the linear unstable global modes.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 3
- Cited by



