Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Qi
Xia, Shu-Ning
Yan, Rui
Sun, De-Jun
and
Wan, Zhen-Hua
2019.
Non-Oberbeck-Boussinesq effects due to large temperature differences in a differentially heated square cavity filled with air.
International Journal of Heat and Mass Transfer,
Vol. 128,
Issue. ,
p.
479.
Mulamootil, J. K.
and
Dash, S. K.
2019.
Significance of non-Oberbeck-Boussinesq effects augmented by power-law rheology in natural convection studies around fins.
Physics of Fluids,
Vol. 31,
Issue. 9,
Demou, Andreas D.
and
Grigoriadis, Dimokratis G. E.
2019.
Direct numerical simulations of Rayleigh–Bénard convection in water with non-Oberbeck–Boussinesq effects.
Journal of Fluid Mechanics,
Vol. 881,
Issue. ,
p.
1073.
Wang, Qi
Zhou, Quan
Wan, Zhen-Hua
and
Sun, De-Jun
2019.
Penetrative turbulent Rayleigh–Bénard convection in two and three dimensions.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
718.
Mulamootil, Jacob Koshy
and
Dash, Sukanta Kumar
2020.
Augmentation and diminution of non-Boussinesq effects due to non-Newtonian power-law behavior in natural convection.
International Journal of Thermal Sciences,
Vol. 151,
Issue. ,
p.
106263.
Wan, Zhen-Hua
Wang, Qi
Wang, Ben
Xia, Shu-Ning
Zhou, Quan
and
Sun, De-Jun
2020.
On non-Oberbeck–Boussinesq effects in Rayleigh–Bénard convection of air for large temperature differences.
Journal of Fluid Mechanics,
Vol. 889,
Issue. ,
Demou, Andreas D.
and
Grigoriadis, Dimokratis G.E.
2020.
Variable property DNS of differentially heated cavities filled with air.
International Journal of Heat and Mass Transfer,
Vol. 149,
Issue. ,
p.
119259.
Mulamootil, Jacob Koshy
Rath, Subhasisa
and
Dash, Sukanta Kumar
2021.
Relative importance of temperature-dependent properties in non-Newtonian natural convection around curved surfaces.
International Communications in Heat and Mass Transfer,
Vol. 124,
Issue. ,
p.
105263.
Wang, Ben
Liu, Shuang
Wan, Zhen-Hua
and
Sun, De-Jun
2021.
Radius ratio dependency of the instability of fully compressible convection in rapidly rotating spherical shells.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
Rath, Subhasisa
2021.
Complex interplay of power-law rheology and non-Oberbeck-Boussinesq effects on natural convection heat transfer in a confined domain.
International Journal of Heat and Mass Transfer,
Vol. 176,
Issue. ,
p.
121462.
Yang, Wenwu
Wan, Zhen-Hua
Zhou, Quan
and
Dong, Yuhong
2022.
On the energy transport and heat transfer efficiency in radiatively heated particle-laden Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 953,
Issue. ,
Pan, Xiaomin
Kim, Ki-Ha
and
Choi, Jung-Il
2022.
Monolithic projection-based method with staggered time discretization for solving non-Oberbeck–Boussinesq natural convection flows.
Journal of Computational Physics,
Vol. 463,
Issue. ,
p.
111238.
Pan, Xiaomin
and
Choi, Jung-Il
2023.
Non-Oberbeck–Boussinesq effects in two-dimensional Rayleigh–Bénard convection of different fluids.
Physics of Fluids,
Vol. 35,
Issue. 9,
Zhang, Jinsong
Wu, Yongyong
Gui, Nan
Yang, Xingtuan
Tu, Jiyuan
and
Jiang, Shengyao
2023.
Investigation of compressible flow under low Mach number in an enclosed square cavity with a novel non-Boussinesq algorithm.
Physics of Fluids,
Vol. 35,
Issue. 12,
Kim, Ki-Ha
Kang, Ji-Hoon
Pan, Xiaomin
and
Choi, Jung-Il
2023.
PaScaL_TCS: A versatile solver for large-scale turbulent convective heat transfer problems with temperature-dependent fluid properties.
Computer Physics Communications,
Vol. 290,
Issue. ,
p.
108779.
Pan, Xiaomin
Yu, Wanli
and
Choi, Jung-Il
2023.
Effects of aspect ratio on Rayleigh–Bénard convection under non-Oberbeck–Boussinesq effects in glycerol.
The European Physical Journal Plus,
Vol. 138,
Issue. 12,
Sun, De-Fa
Wan, Zhen-Hua
and
Sun, De-Jun
2024.
Modulation of Rayleigh–Bénard convection with a large temperature difference by inertial nonisothermal particles.
Physics of Fluids,
Vol. 36,
Issue. 1,
Wu, Chao
Bi, Lin
Zhao, Jin
Tang, Zhigong
Yuan, Xianxu
and
Wen, Dongsheng
2024.
Instability onset of Rayleigh-Bénard convection for diatomic rarefied gases: Effects of molecular interaction models and flow parameters.
International Journal of Heat and Mass Transfer,
Vol. 220,
Issue. ,
p.
124923.
Pan, Xiaomin
and
Choi, Jung-Il
2024.
Effects of inclination angle on Rayleigh–Bénard convection under non-Oberbeck–Boussinesq approximation in air.
International Communications in Heat and Mass Transfer,
Vol. 151,
Issue. ,
p.
107255.
Ke, Junhao
Armfield, S.W.
and
Williamson, N.
2024.
Non-Oberbeck–Boussinesq effects on the linear stability of a vertical natural convection boundary layer.
Journal of Fluid Mechanics,
Vol. 988,
Issue. ,
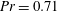 $Pr=0.71$ and contained in two-dimensional rigid cavities of finite aspect ratios. The fluid flow is governed by the low-Mach-number equations, accounting for the NOB effects due to large temperature difference involving flow compressibility and variations of fluid viscosity and thermal conductivity with temperature. The intensity of NOB effects is measured by the dimensionless temperature differential
$Pr=0.71$ and contained in two-dimensional rigid cavities of finite aspect ratios. The fluid flow is governed by the low-Mach-number equations, accounting for the NOB effects due to large temperature difference involving flow compressibility and variations of fluid viscosity and thermal conductivity with temperature. The intensity of NOB effects is measured by the dimensionless temperature differential  $\unicode[STIX]{x1D716}$. Linear stability analysis of the thermal conduction state is performed. An
$\unicode[STIX]{x1D716}$. Linear stability analysis of the thermal conduction state is performed. An 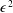 $\unicode[STIX]{x1D716}^{2}$ scaling of the leading-order corrections of critical Rayleigh number
$\unicode[STIX]{x1D716}^{2}$ scaling of the leading-order corrections of critical Rayleigh number 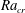 $Ra_{cr}$ and disturbance growth rate
$Ra_{cr}$ and disturbance growth rate  $\unicode[STIX]{x1D70E}$ due to NOB effects is identified, which is a consequence of an intrinsic symmetry of the system. The influences of weak NOB effects on flow instabilities are further studied by perturbation expansion of linear stability equations with regard to
$\unicode[STIX]{x1D70E}$ due to NOB effects is identified, which is a consequence of an intrinsic symmetry of the system. The influences of weak NOB effects on flow instabilities are further studied by perturbation expansion of linear stability equations with regard to  $\unicode[STIX]{x1D716}$, and then the influence of aspect ratio
$\unicode[STIX]{x1D716}$, and then the influence of aspect ratio 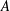 $A$ is investigated in detail. NOB effects are found to enhance (weaken) flow stability in large (narrow) cavities. Detailed contributions of compressibility, viscosity and buoyancy actions on disturbance kinetic energy growth are identified quantitatively by energy analysis. Besides, a weakly nonlinear theory is developed based on centre-manifold reduction to investigate the NOB influences on bifurcation characteristics near convection onset, and amplitude equations are constructed for both codimension-one and -two cases. Rich bifurcation regimes are observed based on amplitude equations and also confirmed by direct numerical simulation. Weakly nonlinear analysis is useful for organizing and understanding these simulation results.
$A$ is investigated in detail. NOB effects are found to enhance (weaken) flow stability in large (narrow) cavities. Detailed contributions of compressibility, viscosity and buoyancy actions on disturbance kinetic energy growth are identified quantitatively by energy analysis. Besides, a weakly nonlinear theory is developed based on centre-manifold reduction to investigate the NOB influences on bifurcation characteristics near convection onset, and amplitude equations are constructed for both codimension-one and -two cases. Rich bifurcation regimes are observed based on amplitude equations and also confirmed by direct numerical simulation. Weakly nonlinear analysis is useful for organizing and understanding these simulation results.


