Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-25T06:21:17.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear amplification of inertial-wave-driven swirl fluctuations in turbulent swirling pipe flows: a resolvent analysis approach

Published online by Cambridge University Press:  05 December 2024

J.S. Müller Open the ORCID record for J.S. Müller [Opens in a new window] ,
J.G.R. von Saldern Open the ORCID record for J.G.R. von Saldern [Opens in a new window] ,
T.L. Kaiser Open the ORCID record for T.L. Kaiser [Opens in a new window]  and
K. Oberleithner Open the ORCID record for K. Oberleithner [Opens in a new window]
J.S. Müller*
Affiliation:
Laboratory for Flow Instabilities and Dynamics, Technische Universität Berlin, Müller-Breslau-Straße 8, 10623 Berlin, Germany
J.G.R. von Saldern
Affiliation:
Laboratory for Flow Instabilities and Dynamics, Technische Universität Berlin, Müller-Breslau-Straße 8, 10623 Berlin, Germany
T.L. Kaiser
Affiliation:
Laboratory for Flow Instabilities and Dynamics, Technische Universität Berlin, Müller-Breslau-Straße 8, 10623 Berlin, Germany
K. Oberleithner
Affiliation:
Laboratory for Flow Instabilities and Dynamics, Technische Universität Berlin, Müller-Breslau-Straße 8, 10623 Berlin, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

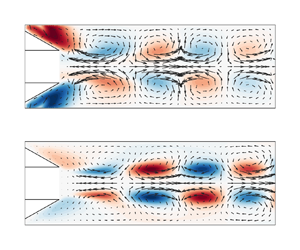
This paper investigates the amplification and propagation of swirl fluctuations in turbulent swirling flows using resolvent analysis. Swirl fluctuations have been repeatedly observed in acoustically excited swirl flows and play a significant role in triggering thermoacoustic instabilities in swirl-stabilized flames. While recent research on simplified rotating laminar base flows suggests that the linear inertial-wave mechanism is a key driver of swirl fluctuations, it remains unclear whether this applies to the fully turbulent regime and whether a linear method is sufficient for modelling. To address this issue, a turbulent swirling pipe flow is considered using large-eddy simulations and phase-locked particle image velocimetry, which are combined with mean-field resolvent analysis. A sound agreement between the empirical and physics-based modes is found in terms of shape and propagation velocity. The latter is particularly important for thermoacoustic time-lag models. The comparison with a generic rotating pipe flow shows that the observed swirl fluctuations are indeed driven by a linear inertial wave mechanism. The resolvent framework is, then, exploited to further investigate the coupling and amplification mechanisms in detail. It is discovered that the combined effects of inertia and strong shear lead to very high amplification rates of the swirl fluctuations, explaining the high potential of these structures to trigger combustion instabilities. The study further demonstrates the capability of the resolvent to reveal the driving mechanisms of flow response structures in highly complex turbulent flows, and it opens the path for efficient physics-based optimization to prevent combustion instabilities.

JFM classification

Turbulent Flows: Pipe flow Turbulent Flows: Rotating turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A91
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abreu, L.I., Tanarro, A., Cavalieri, A.V.G., Schlatter, P., Vinuesa, R., Hanifi, A. & Henningson, D.S. 2021 Spanwise-coherent hydrodynamic waves around flat plates and airfoils. J. Fluid Mech. 927, A1.CrossRefGoogle Scholar
Albayrak, A., Bezgin, D.A. & Polifke, W. 2018 Response of a swirl flame to inertial waves. Intl J. Spray Combust. Dyn. 10 (4), 277–286.CrossRefGoogle Scholar
Albayrak, A., Juniper, M.P. & Polifke, W. 2019 Propagation speed of inertial waves in cylindrical swirling flows. J. Fluid Mech. 879, 85–120.CrossRefGoogle Scholar
Aldridge, K.D. & Lumb, L.I. 1987 Inertial waves identified in the Earth's fluid outer core. Nature 325 (6103), 421–423.CrossRefGoogle Scholar
Alnaes, M.S., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., Richardson, C., Ring, J., Rognes, M.E. & Wells, G.N. 2015 The FEniCS project version 1.5. Arch. Numer. Softw. 3 (100), 9–23.Google Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.CrossRefGoogle Scholar
Beneddine, S., Sipp, D., Arnault, A., Dandois, J. & Lesshafft, L. 2016 Conditions for validity of mean flow stability analysis. J. Fluid Mech. 798, 485–504.CrossRefGoogle Scholar
Benjamin, T.B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14 (4), 593–629.CrossRefGoogle Scholar
Bluemner, R., Paschereit, C.O. & Oberleithner, K. 2019 Generation and transport of equivalence ratio fluctuations in an acoustically forced swirl burner. Combust. Flame 209, 99–116.CrossRefGoogle Scholar
Brandt, L., Sipp, D., Pralits, J.O. & Marquet, O. 2011 Effect of base-flow variation in noise amplifiers: the flat-plate boundary layer. J. Fluid Mech. 687, 503–528.CrossRefGoogle Scholar
Casel, M., Oberleithner, K., Zhang, F., Zirwes, T., Bockhorn, H., Trimis, D. & Kaiser, T.L. 2022 Resolvent-based modelling of coherent structures in a turbulent jet flame using a passive flame approach. Combust. Flame 236, 111695.CrossRefGoogle Scholar
Chomaz, J.M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Colin, O. & Rudgyard, M. 2000 Development of high-order Taylor–Galerkin schemes for LES. J. Comput. Phys. 162 (2), 338–371.CrossRefGoogle Scholar
Fan, Y., Kozul, M., Li, W. & Sandberg, R.D. 2024 Eddy-viscosity-improved resolvent analysis of compressible turbulent boundary layers. J. Fluid Mech. 983, A46.CrossRefGoogle Scholar
Farrell, B.F. & Ioannou, P.J. 2001 Accurate low-dimensional approximation of the linear dynamics of fluid flow. J. Atmos. Sci. 58 (18), 2771–2789.2.0.CO;2>CrossRefGoogle Scholar
Gallaire, F. & Chomaz, J.M. 2003 Instability mechanisms in swirling flows. Phys. Fluids 15 (9), 2622–2639.CrossRefGoogle Scholar
Golubev, V.V. & Atassi, H.M. 1998 Acoustic-vorticity waves in swirling flows. J. Sound Vib. 209 (2), 203–222.CrossRefGoogle Scholar
Greenspan, H.P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hussain, A.K. 1983 Coherent structures - reality and myth. Phys. Fluids 26 (10), 2816–2850.CrossRefGoogle Scholar
Ivanov, P.B. & Papaloizou, J.C. 2010 Inertial waves in rotating bodies: a WKBJ formalism for inertial modes and a comparison with numerical results. Mon. Not. R. Astron. Soc. 407 (3), 1609–1630.CrossRefGoogle Scholar
Ivanova, E.M., Noll, B.E. & Aigner, M. 2013 A numerical study on the turbulent Schmidt numbers in a jet in crossflow. Trans. ASME J. Engng Gas Turbines Power 135 (1), 1–10.CrossRefGoogle Scholar
Jovanović, M.R. & Bamieh, B. 2005 Componentwise energy amplification in channel flows. J. Fluid Mech. 534, 145–183.CrossRefGoogle Scholar
Juniper, M.P. & Sujith, R.I. 2018 Sensitivity and nonlinearity of thermoacoustic oscillations. Annu. Rev. Fluid Mech. 50, 661–689.CrossRefGoogle Scholar
Kaiser, T.L., Demange, S., Müller, J.S., Knechtel, S. & Oberleithner, K. 2023 a FELiCS: a versatile linearized solver addressing dynamics in multi-physics flows. In AIAA Aviation 2023 Forum,p. 3434. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Kaiser, T.L., Lesshafft, L. & Oberleithner, K. 2019 Prediction of the flow response of a turbulent flame to acoustic pertubations based on mean flow resolvent analysis. J. Eng. Gas Turbine. Power 141 (11), 111021.CrossRefGoogle Scholar
Kaiser, T.L., Varillon, G., Polifke, W., Zhang, F., Zirwes, T., Bockhorn, H. & Oberleithner, K. 2023 b Modelling the response of a turbulent jet flame to acoustic forcing in a linearized framework using an active flame approach. Combust. Flame 253, 112778.CrossRefGoogle Scholar
Kerrebrock, J.L. 1977 Small disturbances in turbomachine annuli with swirl. AIAA J. 15 (6), 794–803.CrossRefGoogle Scholar
Khorrami, M.R., Malik, M.R. & Ash, R.L. 1989 Application of spectral collocation techniques to the stability of swirling flows. J. Comput. Phys. 81 (1), 206–229.CrossRefGoogle Scholar
Komarek, T. & Polifke, W. 2010 Impact of swirl fluctuations on the flame response of a perfectly premixed swirl burner. Trans. ASME: J. Engng Gas Turbines Power 132 (6), 1–7.Google Scholar
Kuhn, P., Müller, J.S., Oberleithner, K., Knechtel, S. & Soria, J. 2022 Influence of eddy viscosity on linear modeling of self-similar coherent structures in the jet far field. In AIAA SciTech Forum 2022, p. 0460. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Lehoucq, R.B., Sorensen, D.C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Leuckel, W. 1967 Swirl Intensities, Swirl Types and Energy Losses of Different Swirl Generating Devices. International Flame Research Foundation.Google Scholar
Marquet, O., Lombardi, M., Chomaz, J.M., Sipp, D. & Jacquin, L. 2009 Direct and adjoint global modes of a recirculation bubble: lift-up and convective non-normalities. J. Fluid Mech. 622, 1–21.CrossRefGoogle Scholar
McKeon, B.J. & Sharma, A.S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Morra, P., Semeraro, O., Henningson, D.S. & Cossu, C. 2019 On the relevance of Reynolds stresses in resolvent analyses of turbulent wall-bounded flows. J. Fluid Mech. 867, 969–984.CrossRefGoogle Scholar
Müller, J.S., Lückoff, F., Kaiser, T.L., Paschereit, C.O. & Oberleithner, K. 2022 Modal decomposition and linear modeling of swirl fluctuations in the mixing section of a model combustor based on particle image velocimetry data. Trans. ASME J. Engng Gas Turbines Power 144 (1), 1–10.CrossRefGoogle Scholar
Nicoud, F., Toda, H.B., Cabrit, O., Bose, S. & Lee, J. 2011 Using singular values to build a subgrid-scale model for large eddy simulations. Phys. Fluids 23 (8), 085106.CrossRefGoogle Scholar
Palies, P., Durox, D., Schuller, T. & Candel, S. 2011 a Acoustic-convective mode conversion in an aerofoil cascade. J. Fluid Mech. 672, 545–569.CrossRefGoogle Scholar
Palies, P., Durox, D., Schuller, T. & Candel, S. 2011 b Experimental study on the effect of swirler geometry and swirl number on flame describing functions. Combust. Sci. Technol. 183 (7), 704–717.CrossRefGoogle Scholar
Palies, P., Schuller, T., Durox, D., Gicquel, L.Y. & Candel, S. 2011 c Acoustically perturbed turbulent premixed swirling flames. Phys. Fluids 23 (3), 037101.CrossRefGoogle Scholar
Pickering, E., Rigas, G., Nogueira, P.A., Cavalieri, A.V., Schmidt, O.T. & Colonius, T. 2020 Lift-up, Kelvin–Helmholtz and Orr mechanisms in turbulent jets. J. Fluid Mech. 896, A2.CrossRefGoogle Scholar
Pickering, E., Rigas, G., Schmidt, O.T., Sipp, D. & Colonius, T. 2021 Optimal eddy viscosity for resolvent-based models of coherent structures in turbulent jets. J. Fluid Mech. 917, A29.CrossRefGoogle Scholar
Poinsot, T.J. & Lele, S.K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101 (1), 104–129.CrossRefGoogle Scholar
Qadri, U.A. & Schmid, P.J. 2017 Frequency selection mechanisms in the flow of a laminar boundary layer over a shallow cavity. Phys. Rev. Fluids 2 (1), 1–18.CrossRefGoogle Scholar
Reau, N. & Tumin, A. 2002 Harmonic perturbations in turbulent wakes. AIAA J. 40 (3), 526–530.CrossRefGoogle Scholar
Renac, F., Sipp, D. & Jacquin, L. 2007 Criticality of compressible rotating flows. Phys. Fluids 19 (1), 018101.CrossRefGoogle Scholar
Reynolds, W.C. & Hussain, A.K.M.F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (02), 263–288.CrossRefGoogle Scholar
Rukes, L., Paschereit, C.O. & Oberleithner, K. 2016 An assessment of turbulence models for linear hydrodynamic stability analysis of strongly swirling jets. Eur. J. Mech. (B/Fluids) 59, 205–218.CrossRefGoogle Scholar
Schmidt, O.T., Towne, A., Rigas, G., Colonius, T. & Brès, G.A. 2018 Spectral analysis of jet turbulence. J. Fluid Mech. 855, 953–982.CrossRefGoogle Scholar
Selle, L., Nicoud, F. & Poinsot, T. 2004 Actual impedance of nonreflecting boundary conditions: implications for computation of resonators. AIAA J. 42 (5), 958–964.CrossRefGoogle Scholar
Sipp, D. & Marquet, O. 2013 Characterization of noise amplifiers with global singular modes: the case of the leading-edge flat-plate boundary layer. Theor. Comput. Fluid Dyn. 27 (5), 617–635.CrossRefGoogle Scholar
Symon, S., Illingworth, S.J. & Marusic, I. 2021 Energy transfer in turbulent channel flows and implications for resolvent modelling. J. Fluid Mech. 911, A3.CrossRefGoogle Scholar
Symon, S., Madhusudanan, A., Illingworth, S.J. & Marusic, I. 2023 Use of eddy viscosity in resolvent analysis of turbulent channel flow. Phys. Rev. Fluids 8 (6), 064601.CrossRefGoogle Scholar
Symon, S., Rosenberg, K., Dawson, S.T. & McKeon, B.J. 2018 Non-normality and classification of amplification mechanisms in stability and resolvent analysis. Phys. Rev. Fluids 3 (5), 1–33.CrossRefGoogle Scholar
Symon, S., Sipp, D. & McKeon, B.J. 2019 A tale of two airfoils: resolvent-based modelling of an oscillator vs. an amplifier from an experimental mean. J. Fluid Mech. 881, 51–83.CrossRefGoogle Scholar
Tam, C.K. & Auriault, L. 1998 The wave modes in ducted swirling flows. J. Fluid Mech. 371, 1–20.CrossRefGoogle Scholar
Tammisola, O. & Juniper, M.P. 2016 Coherent structures in a swirl injector at $Re = 4800$ by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.CrossRefGoogle Scholar
Turton, S.E., Tuckerman, L.S. & Barkley, D. 2015 Prediction of frequencies in thermosolutal convection from mean flows. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 91 (4), 1–10.CrossRefGoogle ScholarPubMed
Wang, S. & Rusak, Z. 1996 On the stability of an axisymmetric rotating flow in a pipe. Phys. Fluids 8 (4), 1007–1016.CrossRefGoogle Scholar