Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-06T06:09:41.557Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-scale motions in turbulent boundary layers subjected to adverse pressure gradients

Published online by Cambridge University Press:  25 November 2016

Jae Hwa Lee
Jae Hwa Lee*
Affiliation:
School of Mechanical and Nuclear Engineering, UNIST, 50 UNIST-gil, Eonyang-eup, Ulsan 44919, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is known that large-scale streamwise velocity-fluctuating structures (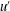$u^{\prime }$) are frequently observed in the log region of a zero pressure gradient turbulent boundary layer, and that these motions significantly influence near-wall small-scale 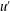$u^{\prime }$-structures by modulating the amplitude (Hutchins & Marusic, J. Fluid Mech., vol. 579, 2007, pp. 1–28; Mathis et al., J. Fluid Mech., vol. 628, 2009, pp. 311–337). In the present study, we provide evidence that the spatial organization of large-scale structures in the log region is significantly influenced by the strength of adverse pressure gradients in turbulent boundary layers based on a direct numerical simulation dataset. For a mild adverse pressure gradient boundary layer flow, groups of hairpin vortices are coherently aligned in the streamwise direction to form hairpin vortex packets, and streamwise merging events of the induced large-scale 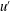$u^{\prime }$-structures create a larger streamwise length scale of structures than that for a zero pressure gradient boundary layer flow. As the pressure gradient strength increases further, however, the formation of hairpin packets is continuously suppressed, and large-scale motions are consequently not concatenated to create a longer motion, resulting in a significant reduction of the streamwise coherence of large-scale structures in the log layer. Although energy spectrum maps for 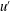$u^{\prime }$-structures show that the large-scale energy is continuously intensified above the log layer with an increase in the pressure gradient, amplitude modulation of the near-wall small-scale motions is dominantly induced by log region large-scale structures for adverse pressure gradient flows. Conditional averaged flow fields with large-scale Q2 and Q4 events indicate that large-scale counter-rotating roll modes play an important role in organizing the flows under the pressure gradients, and the large-scale roll modes associated with Q4 events are more enhanced in the outer layer than those associated with Q2 events, reducing the streamwise coherence of the vortices in a packet.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 810 , 10 January 2017 , pp. 323 - 361
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Re 𝜏 = 640. Trans. ASME J. Fluids Engng 126, 835–843.CrossRefGoogle Scholar
Adrian, R. J. 1996 Stochastic estimation of the structure of turbulent fields. In Eddy Structure Identification (ed. Bonnet, J. P.), pp. 145–196. Springer.CrossRefGoogle Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.CrossRefGoogle Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. A 365, 665–681.CrossRefGoogle ScholarPubMed
Baltzer, J. R., Adrian, R. J. & Wu, X. 2013 Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236–279.Google Scholar
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27, 2221–2228.Google Scholar
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer layer interactions in turbulent boundary layers: a refined measure of the large-scale amplitude modulation mechanism. Phys. Fluids 23, 061701.Google Scholar
Bradshaw, P. 1967 The turbulence structure of equilibrium boundary layers. J. Fluid Mech. 29, 628–645.CrossRefGoogle Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.CrossRefGoogle Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Dennis, J. C. D. & Nickels, T. B. 2011a Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2011b Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.CrossRefGoogle Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.CrossRefGoogle Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.Google Scholar
Hoyas, S. & Jimenez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18, 011702.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google ScholarPubMed
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wider outer motions. J. Fluid Mech. 723, 264–288.Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Jodai, Y. & Elsinga, G. E. 2016 Experimental observation of hairpin auto-generation events in a turbulent boundary layer. J. Fluid Mech. 795, 611–633.CrossRefGoogle Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kim, K., Baek, S.-J. & Sung, H. J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38, 125–138.CrossRefGoogle Scholar
Krogstad, P.-Å. & Skåre, P. E. 1995 Influence of a strong adverse pressure gradient on the turbulent structure in a boundary layer. Phys. Fluids 7, 2014–2024.CrossRefGoogle Scholar
Lee, J., Kim, J. H. & Lee, J. H. 2016 Scale growth of structures in the turbulent boundary layer with a rod-roughened wall. Phys. Fluids 28, 015104.Google Scholar
Lee, J., Lee, J. H., Choi, J.-I. & Sung, H. J. 2014 Spatial organization of large- and very-large-scale motions in a turbulent channel flow. J. Fluid Mech. 749, 818–840.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2008 Effects of an adverse pressure gradient on a turbulent boundary layer. Intl J. Heat Fluid Flow 29, 568–578.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2009 Structures in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 639, 101–131.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.CrossRefGoogle Scholar
Lu, S. S. & Willmarth, W. W. 1973 Measurement of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481–511.CrossRefGoogle Scholar
Lund, T. S., Wu, X. & Squires, K. D. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140, 233–258.Google Scholar
Marquillie, M., Ehrenstein, U. & Laval, J.-P. 2011 Instability of streaks in wall turbulence with adverse pressure gradient. J. Fluid Mech. 681, 205–240.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mellor, G. L. & Gibson, D. M. 1966 Equilibrium turbulent boundary layers. J. Fluid Mech. 24, 225–253.Google Scholar
Monty, J. P., Harun, Z. & Marusic, I. 2011 A parameter study of adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 32, 568–578.Google Scholar
Na, Y. & Moin, P. 1998 The structure of wall-pressure fluctuations in turbulent boundary layers with adverse pressure gradient and separation. J. Fluid Mech. 377, 347–373.Google Scholar
Nagano, Y., Tagawa, M. & Tsuji, T. 1993 Effects of adverse pressure gradients on mean flows and turbulence statistics in a boundary layer. In Turbulent Shear Flows (ed. Durst, F., Friedrich, R., Launder, B. E., Schmidt, F. W., Schumann, U. & Whitelaw, J. H.), vol. 8, pp. 7–21. Springer.Google Scholar
Rahgozar, S. & Maciel, Y. 2011 Low- and high-speed structures in the outer region of an adverse-pressure-gradient turbulent boundary layer. Exp. Therm. Fluid Sci. 35, 1575–1587.CrossRefGoogle Scholar
Schlatter, P. & Őrlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.CrossRefGoogle Scholar
Skåre, P. E. & Krogstad, P.-Å. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.CrossRefGoogle Scholar
Skote, M., Henkes, R. A. W. M. & Henningson, D. S. 1998 Direct numerical simulation of self-similar turbulent boundary layers in adverse pressure gradient. Flow Turbul. Combust. 60, 47–85.Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to R 𝜃 = 1410. J. Fluid Mech. 187, 61–98.Google Scholar
Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524, 249–262.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Wallace, J. M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48, 131–158.CrossRefGoogle Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a 30R long turbulent pipe flow at R + = 685: large- and very large-scale motions. J. Fluid Mech. 698, 235–281.CrossRefGoogle Scholar
Wu, X. & Moin, P. 2010 Transitional and turbulent boundary layer with heat transfer. Phys. Fluids 22, 085105.CrossRefGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices. J. Fluid Mech. 387, 353–396.Google Scholar