Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T07:22:47.903Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-scale motions in a plane wall jet

Published online by Cambridge University Press:  19 August 2019

Ebenezer P. Gnanamanickam Open the ORCID record for Ebenezer P. Gnanamanickam [Opens in a new window] ,
Shibani Bhatt Open the ORCID record for Shibani Bhatt [Opens in a new window] ,
Sravan Artham Open the ORCID record for Sravan Artham [Opens in a new window]  and
Zheng Zhang Open the ORCID record for Zheng Zhang [Opens in a new window]
Ebenezer P. Gnanamanickam*
Affiliation:
Department of Aerospace Engineering, Embry-Riddle Aeronautical University, FL 32114, USA
Shibani Bhatt
Affiliation:
Department of Aerospace Engineering, Embry-Riddle Aeronautical University, FL 32114, USA
Sravan Artham
Affiliation:
Department of Aerospace Engineering, Embry-Riddle Aeronautical University, FL 32114, USA
Zheng Zhang
Affiliation:
Department of Aerospace Engineering, Embry-Riddle Aeronautical University, FL 32114, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The plane wall jet (PWJ) is a wall-bounded flow in which a wall shear layer develops in the presence of extremely energetic flow structures of the outer free-shear layer. The structure of a PWJ, developing in still air, was studied with the focus on the large scales in the flow. Wall-normal hot-wire anemometry (HWA) measurements along with double-frame particle image velocimetry (PIV) measurements (wall-normal–streamwise plane) were carried out at streamwise distances up to 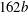$162b$, where 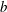$b$ is the slot width of the PWJ exit. The nominal PWJ Reynolds number based on exit parameters was 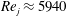$Re_{j}\approx 5940$. Comparisons with a zero-pressure-gradient boundary layer (ZPGBL) at nominally matched friction Reynolds number 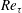$Re_{\unicode[STIX]{x1D70F}}$ were also carried out as appropriate, to highlight key features of the PWJ structure. Consistent with previous work, the PWJ showed a dependence of the peak turbulent stresses on the jet exit Reynolds number. The turbulent production showed a peak corresponding to the near-wall cycle similar to the peak seen in the ZPGBL. However, another turbulent production peak was observed in the outer free-shear layer that was an order of magnitude larger than the inner one. Along with the change in sign of the viscous and Reynolds shear stresses, the PWJ was shown to have a region of very low turbulent production between these two peaks. The dissipation rate increased over the PWJ layer with a peak also in the outer region. Visualizations of the flow and two-point correlations reveal that the most energetic large-scale structures within a PWJ are vortical motions in the wall-normal–streamwise plane similar to those structures seen in free-shear layers. These structures are referred to as J (for jet) type structures. In addition two-point correlations reveal the existence of large-scale structures in the wall region which have a signature similar to those structures seen in canonical boundary layers. These structures are referred to as W (for wall) type structures. Instantaneous PIV realizations and flow visualizations reveal that these W type large-scale features are consistent with the paradigm of hairpin vortex packets in the wall region. The J type structures were seen to intrude well into the wall region while the W type structures were also seen to extend into the outer shear layer. Further, these large-scale structures were shown to modulate the amplitude of the finer scales of the flow.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 877 , 25 October 2019 , pp. 239 - 281
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abrahamsson, H., Johansson, B. & Löfdahl, L. 1994 A turbulent plane two-dimensional wall-jet in a quiescent surrounding. Eur. J. Mech. (B/Fluids) 13, 533–556.Google Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.10.1063/1.2717527Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.10.1017/S0022112000001580Google Scholar
Ahlman, D., Brethouwer, G. & Johansson, A. V. 2007 Direct numerical simulation of a plane turbulent wall-jet including scalar mixing. Phys. Fluids 19 (6), 065102.10.1063/1.2732460Google Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.10.1017/S0022112006000607Google Scholar
Baars, W. J., Talluru, K. M., Hutchins, N. & Marušić, I. 2015 Wavelet analysis of wall turbulence to study large-scale modulation of small scales. Exp. Fluids 56 (10), 188.10.1007/s00348-015-2058-8Google Scholar
Baidya, R.2016 Multi-component velocity measurements in turbulent boundary layers. PhD thesis, The University of Melbourne.Google Scholar
Bailey, S. C. C. & Smits, A. J. 2010 Experimental investigation of the structure of large- and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 651, 339–356.10.1017/S0022112009993983Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.10.1098/rsta.2006.1940Google Scholar
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27 (9), 2221–2228.10.1063/1.864901Google Scholar
Banyassady, R. & Piomelli, U. 2014 Turbulent plane wall jets over smooth and rough surfaces. J. Turbul. 15 (3), 186–207.10.1080/14685248.2014.888492Google Scholar
Banyassady, R. & Piomelli, U. 2015 Interaction of inner and outer layers in plane and radial wall jets. J. Turbul. 16 (5), 460–483.10.1080/14685248.2015.1008008Google Scholar
Bradshaw, B. A. & Gee, M. T. 1960 Turbulent wall jets with and without an external stream. NPL Bull. 3252, 51.Google Scholar
Browand, F. K. 1986 The structure of the turbulent mixing layer. Physica D 18 (1), 135–148.10.1016/0167-2789(86)90168-5Google Scholar
Brown, G. L. & Thomas, A. S. W. 1977 Large structure in a turbulent boundary layer. Phys. Fluids 20 (10), S243–S252.10.1063/1.861737Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.Google Scholar
Christensen, K. T.2001 Experimental investigation of acceleration and velocity fields in turbulent channel flow. PhD thesis, University of Illinois at Urbana-Champaign.Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.10.1017/S0022112001003512Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.10.1017/S0022112010002995Google Scholar
De Graaff, D. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.10.1017/S0022112000001713Google Scholar
Dejoan, A. & Leschziner, M. A. 2005 Large eddy simulation of a plane turbulent wall jet. Phys. Fluids 17 (2), 025102.10.1063/1.1833413Google Scholar
Dejoan, A. & Leschziner, M. A. 2006 Separating the effects of wall blocking and near-wall shear in the interaction between the wall and the free shear layer in a wall jet. Phys. Fluids 18 (6), 065110.10.1063/1.2212991Google Scholar
Dejoan, A. & Leschziner, M. A. 2007 On the near-wall structure in reverse-flow and post-reattachment recovery regions of separated flow and its equivalence to the structure in wall and free-surface jets. J. Turbul. 8, N14.10.1080/14685240701199783Google Scholar
Dogan, E., Hanson, R. E. & Ganapathisubramani, B. 2016 Interactions of large-scale free-stream turbulence with turbulent boundary layers. J. Fluid Mech. 802, 79–107.10.1017/jfm.2016.435Google Scholar
Dunn, M.2010 An experimental study of a plane turbulent wall jet using particle image velocimetry. Master’s thesis, University of Saskatchewan.Google Scholar
Duvvuri, S. & McKeon, B. J. 2015 Triadic scale interactions in a turbulent boundary layer. J. Fluid Mech. 767, R4.10.1017/jfm.2015.79Google Scholar
Eriksson, J. G., Karlsson, R. I. & Persson, J. 1998 An experimental study of a two-dimensional plane turbulent wall jet. Exp. Fluids 25 (1), 50–60.10.1007/s003480050207Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marušić, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.10.1017/jfm.2012.398Google Scholar
George, W. K., Abrahamsson, H., Eriksson, J., Karlsson, R. I., Löfdahl, L. & Wosnik, M. 2000 A similarity theory for the turbulent plane wall jet without external stream. J. Fluid Mech. 425, 367–411.10.1017/S002211200000224XGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.10.1017/S0022112006008871Google Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2011 Interactions within the turbulent boundary layer at high Reynolds number. J. Fluid Mech. 666, 573–604.10.1017/S0022112010004544Google Scholar
Hammond, G. P. 1982 Complete velocity profile and ‘optimum’ skin friction formulas for the plane wall-jet. Trans. ASME J. Fluids Engng 104, 59–65.10.1115/1.3240855Google Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marušić, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.10.1017/jfm.2012.531Google Scholar
Hearst, R. J., Dogan, E. & Ganapathisubramani, B. 2018 Robust features of a turbulent boundary layer subjected to high-intensity free-stream turbulence. J. Fluid Mech. 851, 416–435.10.1017/jfm.2018.511Google Scholar
Hutchins, N. & Choi, K.-S. 2002 Robust features of a turbulent boundary layer subjected to high-intensity free-stream turbulence. Prog. Aerosp. Sci. 38 (4–5), 421–446.10.1016/S0376-0421(02)00027-1Google Scholar
Hutchins, N. & Marušić, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.10.1017/S0022112006003946Google Scholar
Hutchins, N. & Marušić, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.10.1098/rsta.2006.1942Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marušić, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.10.1017/S0022112010006245Google Scholar
Hutchins, N., Nickels, T. B., Marušić, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.10.1017/S0022112009007721Google Scholar
Irwin, H. P. A. H. 1973 Measurements in a self-preserving plane wall jet in a positive pressure gradient. J. Fluid Mech. 61 (1), 33–63.10.1017/S0022112073000558Google Scholar
Jacobi, I. & McKeon, B. J. 2013 Phase relationships between large and small scales in the turbulent boundary layer. Exp. Fluids 54 (3), 1481.10.1007/s00348-013-1481-yGoogle Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.10.1146/annurev-fluid-120710-101039Google Scholar
Karlsson, R. I., Eriksson, J. & Persson, J.1993a An experimental study of a two-dimensional plane turbulent wall jet. Tech. Rep. Report VU-S 93:B36. Vattenfall Utveckling AB, lvkarleby, Sweden.Google Scholar
Karlsson, R. I., Eriksson, J. & Persson, J. 1993b LDV measurements in a plane wall jet in a large enclosure. In Laser Techniques and Applications in Fluid Mechanics: Proceedings of the 6th International Symposium, Lisbon, Portugal, 20–23, July 1992.Google Scholar
Katz, Y., Horev, E. & Wygnanski, I. 1992 The forced turbulent wall jet. J. Fluid Mech. 242, 577–609.10.1017/S0022112092002507Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.10.1017/S0022112067001740Google Scholar
Kulandaivelu, V.2011 Evolution and structure of zero pressure gradient turbulent boundary layer. PhD thesis, University of Melbourne.Google Scholar
Launder, B. E. & Rodi, W. 1981 The turbulent wall jet. Prog. Aerosp. Sci. 19, 81–128.10.1016/0376-0421(79)90002-2Google Scholar
Launder, B. E. & Rodi, W. 1983 The turbulent wall jet measurements and modeling. Annu. Rev. Fluid Mech. 15 (1), 429–459.10.1146/annurev.fl.15.010183.002241Google Scholar
Lee, J. H. & Sung, H. J. 2013 Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids 25 (4), 045103.10.1063/1.4802048Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.10.1017/jfm.2015.268Google Scholar
Loucks, R. B. & Wallace, J. M. 2012 Velocity and velocity gradient based properties of a turbulent plane mixing layer. J. Fluid Mech. 699, 280–319.10.1017/jfm.2012.103Google Scholar
Marušić, I. & Heuer, W. D. C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99 (11), 114504.10.1103/PhysRevLett.99.114504Google Scholar
Marušić, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.10.1063/1.3453711Google Scholar
Mathis, R., Hutchins, N. & Marušić, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.10.1017/S0022112009006946Google Scholar
Mathis, R., Hutchins, N. & Marušić, I. 2011a A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.10.1017/jfm.2011.216Google Scholar
Mathis, R., Marušić, I., Hutchins, N. & Sreenivasan, K. R. 2011b The relationship between the velocity skewness and the amplitude modulation of the small scale by the large scale in turbulent boundary layers. Phys. Fluids 23 (12), 121702.10.1063/1.3671738Google Scholar
Mathis, R., Monty, J. P., Hutchins, N. & Marušić, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21 (11), 111703.10.1063/1.3267726Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marušić, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.10.1017/S0022112009007423Google Scholar
Naqavi, I. Z., Tyacke, J. C. & Tucker, P. G. 2018 Direct numerical simulation of a wall jet: flow physics. J. Fluid Mech. 852, 507–542.10.1017/jfm.2018.503Google Scholar
Narasimha, R., Narayan, K. Y. & Parthasarathy, S. P. 1973 Parametric analysis of turbulent wall jets in still air. Aeronaut. J. 77, 335–359.Google Scholar
Nugroho, B., Hutchins, N. & Monty, J. P. 2013 Large-scale spanwise periodicity in a turbulent boundary layer induced by highly ordered and directional surface roughness. Intl J. Heat Fluid Flow 41, 90–102.10.1016/j.ijheatfluidflow.2013.04.003Google Scholar
Pathikonda, G. & Christensen, K. T. 2017 Inner-outer interactions in a turbulent boundary layer overlying complex roughness. Phys. Rev. Fluids 2, 044603.10.1103/PhysRevFluids.2.044603Google Scholar
Perot, B. & Moin, P. 1995 Shear-free turbulent boundary layers. Part 1. Physical insights into near-wall turbulence. J. Fluid Mech. 295, 199–227.10.1017/S0022112095001935Google Scholar
Pope, S. B. 2001 Turbulent Flows. IOP Publishing.Google Scholar
Rauleder, J. & Leishman, J. G. 2014 Flow environment and organized turbulence structures near a plane below a rotor. AIAA J. 52 (1), 146–161.10.2514/1.J052315Google Scholar
Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6 (2), 903–923.10.1063/1.868325Google Scholar
Rostamy, N., Bergstrom, D. J., Sumner, D. & Bugg, J. D. 2011a The effect of surface roughness on the turbulence structure of a plane wall jet. Phys. Fluids 23 (8), 2043–2050.10.1063/1.3614478Google Scholar
Rostamy, N., Bergstrom, D. J., Sumner, D. & Bugg, J. D. 2011b An experimental study of a turbulent wall jet on smooth and transitionally rough surfaces. J. Fluids Engng 133 (11), 111207.Google Scholar
Samie, M., Marušić, I., Hutchins, N., Fu, M. K., Fan, Y., Hultmark, M. & Smits, A. J. 2018 Fully resolved measurements of turbulent boundary layer flows up to Re 𝜏 = 20 000. J. Fluid Mech. 851, 391–415.10.1017/jfm.2018.508Google Scholar
Schlatter, P. & Orlu, R. 2010 Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22 (5), 1–4.10.1063/1.3432488Google Scholar
Schneider, M. E. & Goldstein, R. J. 1994 Laser Doppler measurement of turbulence parameters in a two-dimensional plane wall jet. Phys. Fluids 6 (9), 3116–3129.10.1063/1.868136Google Scholar
Schober, M. & Fernholz, H.-H. 2000 Turbulence control in wall jets. Eur. J. Mech. (B/Fluids) 19 (4), 503–528.10.1016/S0997-7546(00)00131-XGoogle Scholar
Sharp, N. S., Neuscamman, S. & Warhaft, Z. 2009 Effects of large-scale free stream turbulence on a turbulent boundary layer. Phys. Fluids 21 (9), 095105.10.1063/1.3225146Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25 (10), 105102.10.1063/1.4823831Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 26 (10), 105109.10.1063/1.4899259Google Scholar
Smith, B.2008 Wall jet boundary layer flows over smooth and rough surfaces. PhD thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA.Google Scholar
Smits, A. J., McKeon, B. J. & Marušić, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.10.1146/annurev-fluid-122109-160753Google Scholar
Tachie, M., Balachandar, R. & Bergstrom, D. 2002 Scaling the inner region of turbulent plane wall jets. Exp. Fluids 33 (2), 351–354.10.1007/s00348-002-0451-6Google Scholar
Tachie, M. F., Balachandar, R. & Bergstrom, D. J. 2004 Roughness effects on turbulent plane wall jets in an open channel. Exp. Fluids 37 (2), 281–292.10.1007/s00348-004-0816-0Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marušić, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.10.1017/jfm.2014.132Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tutkun, M., George, W. K., Delville, J., Stanislas, M., Johansson, P. B. V., Foucaut, J.-M. & Coudert, S. 2009 Two-point correlations in high Reynolds number flat plate turbulent boundary layers. J. Turbul. 10, N21.10.1080/14685240902878045Google Scholar
Venås, B., Abrahamsson, H., Krogstad, P. Å & Löfdahl, L. 1999 Pulsed hot-wire measurements in two- and three-dimensional wall jets. Exp. Fluids 27 (3), 210–218.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough-and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.10.1017/S0022112007008518Google Scholar
Wu, Y. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.10.1017/S0022112010000960Google Scholar
Wygnanski, I., Katz, Y. & Horev, E. 1992 On the applicability of various scaling laws to the turbulent wall jet. J. Fluid Mech. 234, 669–690.10.1017/S002211209200096XGoogle Scholar
Zhou, M. D., Heine, C. & Wygnanski, I. 1993 The forced turbulent wall jet in an external stream. In 3rd Shear Flow Conference, Orlando, FL. AIAA Paper 93-3250. AIAA.Google Scholar
Zhou, M. D., Heine, C. & Wygnanski, I. 1996 The effects of excitation on the coherent and random motion in a plane wall jet. J. Fluid Mech. 310, 1–37.10.1017/S0022112096001711Google Scholar

Gnanamanickam et al. supplementary movie 1

Large-scale temporal evolution of the flow. Here, nominal values of the relevant scales at $x/b=137$ have been used to carry out non-dimensionalization. Also shown are the nominal locations of the outer length scale $\delta$ and the location of the maximum velocity $z_m$ at $x/b=137$.

Download Gnanamanickam et al. supplementary movie 1(Video)
Video 31.7 MB

Gnanamanickam et al. supplementary movie 2

Identical to Movie 1 but with two zoomed-in views of the near-wall region, highlighting specific instantaneous flow structures. Here, nominal values of the relevant scales at $x/b=137$ have been used to carry out non-dimensionalization. Also shown are the nominal locations of the outer length scale $\delta$ and the location of the maximum velocity $z_m$ at $x/b=137$.

Download Gnanamanickam et al. supplementary movie 2(Video)
Video 18.1 MB