Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Huang, Shi-Di
and
Xia, Ke-Qing
2016.
Effects of geometric confinement in quasi-2-D turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 794,
Issue. ,
p.
639.
Castillo-Castellanos, Andres
Sergent, Anne
and
Rossi, Maurice
2016.
Reversal cycle in square Rayleigh–Bénard cells in turbulent regime.
Journal of Fluid Mechanics,
Vol. 808,
Issue. ,
p.
614.
Xi, Heng-Dong
Zhang, Yi-Bao
Hao, Jian-Tao
and
Xia, Ke-Qing
2016.
Higher-order flow modes in turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 805,
Issue. ,
p.
31.
Xia, Shu-Ning
Wan, Zhen-Hua
Liu, Shuang
Wang, Qi
and
Sun, De-Jun
2016.
Flow reversals in Rayleigh–Bénard convection with non-Oberbeck–Boussinesq effects.
Journal of Fluid Mechanics,
Vol. 798,
Issue. ,
p.
628.
Zhang, Yang
Huang, Yong-Xiang
Jiang, Nan
Liu, Yu-Lu
Lu, Zhi-Ming
Qiu, Xiang
and
Zhou, Quan
2017.
Statistics of velocity and temperature fluctuations in two-dimensional Rayleigh-Bénard convection.
Physical Review E,
Vol. 96,
Issue. 2,
Mannattil, Manu
Pandey, Ambrish
Verma, Mahendra K.
and
Chakraborty, Sagar
2017.
On the applicability of low-dimensional models for convective flow reversals at extreme Prandtl numbers.
The European Physical Journal B,
Vol. 90,
Issue. 12,
Podvin, Bérengère
and
Sergent, Anne
2017.
Precursor for wind reversal in a square Rayleigh-Bénard cell.
Physical Review E,
Vol. 95,
Issue. 1,
Fauve, Stéphan
Herault, Johann
Michel, Guillaume
and
Pétrélis, François
2017.
Instabilities on a turbulent background.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2017,
Issue. 6,
p.
064001.
Podvin, Bérengère
and
Fraigneau, Yann
2017.
A few thoughts on proper orthogonal decomposition in turbulence.
Physics of Fluids,
Vol. 29,
Issue. 2,
Giannakis, Dimitrios
Kolchinskaya, Anastasiya
Krasnov, Dmitry
and
Schumacher, Jörg
2018.
Koopman analysis of the long-term evolution in a turbulent convection cell.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
735.
De, A.K.
Eswaran, V.
and
Mishra, P.K.
2018.
Dynamics of plumes in turbulent Rayleigh–Bénard convection.
European Journal of Mechanics - B/Fluids,
Vol. 72,
Issue. ,
p.
164.
Pandey, Ambrish
Verma, Mahendra K.
and
Barma, Mustansir
2018.
Reversals in infinite-Prandtl-number Rayleigh-Bénard convection.
Physical Review E,
Vol. 98,
Issue. 2,
Wang, Qi
Xia, Shu-Ning
Wang, Bo-Fu
Sun, De-Jun
Zhou, Quan
and
Wan, Zhen-Hua
2018.
Flow reversals in two-dimensional thermal convection in tilted cells.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
355.
Rao, Anirudh N.
Minelli, Guglielmo
Zhang, Jie
Basara, Branislav
and
Krajnović, Siniša
2018.
Investigation of the near-wake flow topology of a simplified heavy vehicle using PANS simulations.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 183,
Issue. ,
p.
243.
Xiao, Yue
Tao, Jianjun
Ma, Xue
and
Xiong, Xiangming
2018.
Oscillating convection and reversal flow in connected cavities.
Physical Review E,
Vol. 98,
Issue. 6,
Takeuchi, Shintaro
Miyamori, Yuri
Gu, Jingchen
and
Kajishima, Takeo
2019.
Flow reversals in particle-dispersed natural convection in a two-dimensional enclosed square domain.
Physical Review Fluids,
Vol. 4,
Issue. 8,
Faranda, D.
Podvin, B.
and
Sergent, A.
2019.
On reversals in 2D turbulent Rayleigh-Bénard convection: Insights from embedding theory and comparison with proper orthogonal decomposition analysis.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 29,
Issue. 3,
Soucasse, Laurent
Podvin, Bérengère
Rivière, Philippe
and
Soufiani, Anouar
2019.
Proper orthogonal decomposition analysis and modelling of large-scale flow reorientations in a cubic Rayleigh–Bénard cell.
Journal of Fluid Mechanics,
Vol. 881,
Issue. ,
p.
23.
Castillo-Castellanos, Andrés
Sergent, Anne
Podvin, Bérengère
and
Rossi, Maurice
2019.
Cessation and reversals of large-scale structures in square Rayleigh–Bénard cells.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
922.
Chen, Xin
Huang, Shi-Di
Xia, Ke-Qing
and
Xi, Heng-Dong
2019.
Emergence of substructures inside the large-scale circulation induces transition in flow reversals in turbulent thermal convection.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
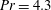 $\mathit{Pr}=4.3$
) at a turbulent Rayleigh number of
$\mathit{Pr}=4.3$
) at a turbulent Rayleigh number of
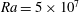 $\mathit{Ra}=5\times 10^{7}$
. We focus on the structures and dynamics of the large-scale intermittent flow. Two quasi-stable flow patterns are identified: one consists of a main diagonal roll with two corner rolls; and the other of two horizontally stacked rolls. These stable flow structures are associated with two types of events, which involve corner flow growth and pattern rotation: reversals, when the main roll rapidly switches signs; and cessations, when it disappears for longer periods. Proper orthogonal decomposition (POD) is applied independently to the velocity field and to the temperature field. In both cases, three principal modes were identified: a single-roll, large-scale circulation; a quadrupolar flow; and a double-roll, symmetry-breaking mode. The large-scale circulation is the kinetic mode with the highest energy. The most energetic temperature mode is associated with the mean temperature and corresponds to a velocity field of quadrupolar nature. The vertical heat flux is concentrated in these two modes. The reversal process is characterized by sharp fluctuations in the amplitudes of all modes. Analysis of the interaction coefficients between the spatial modes leads us to propose a three-dimensional model, based on the interaction of the large-scale circulation, the quadrupolar flow and horizontal rolls. The main dynamics and time scales of reversals and cessations are reproduced by the model in the presence of noise.
$\mathit{Ra}=5\times 10^{7}$
. We focus on the structures and dynamics of the large-scale intermittent flow. Two quasi-stable flow patterns are identified: one consists of a main diagonal roll with two corner rolls; and the other of two horizontally stacked rolls. These stable flow structures are associated with two types of events, which involve corner flow growth and pattern rotation: reversals, when the main roll rapidly switches signs; and cessations, when it disappears for longer periods. Proper orthogonal decomposition (POD) is applied independently to the velocity field and to the temperature field. In both cases, three principal modes were identified: a single-roll, large-scale circulation; a quadrupolar flow; and a double-roll, symmetry-breaking mode. The large-scale circulation is the kinetic mode with the highest energy. The most energetic temperature mode is associated with the mean temperature and corresponds to a velocity field of quadrupolar nature. The vertical heat flux is concentrated in these two modes. The reversal process is characterized by sharp fluctuations in the amplitudes of all modes. Analysis of the interaction coefficients between the spatial modes leads us to propose a three-dimensional model, based on the interaction of the large-scale circulation, the quadrupolar flow and horizontal rolls. The main dynamics and time scales of reversals and cessations are reproduced by the model in the presence of noise.


