Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T14:50:33.440Z Has data issue: false hasContentIssue false
  • English
  • Français

A large-eddy simulation on a deep-stalled aerofoil with a wavy leading edge

Published online by Cambridge University Press:  17 January 2017

Rafael Pérez-Torró  and
Jae Wook Kim
Rafael Pérez-Torró
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
Jae Wook Kim*
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

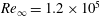A numerical investigation on the stalled flow characteristics of a NACA0021 aerofoil with a sinusoidal wavy leading edge (WLE) at chord-based Reynolds number $Re_{\infty }=1.2\times 10^{5}$ and angle of attack 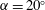$\unicode[STIX]{x1D6FC}=20^{\circ }$ is presented in this paper. It is observed that laminar separation bubbles (LSBs) form at the trough areas of the WLE in a collocated fashion rather than uniformly/periodically distributed over the span. It is found that the distribution of LSBs and their influence on the aerodynamic forces is strongly dependent on the spanwise domain size of the simulation, i.e. the wavenumber of the WLE used. The creation of a pair of counter-rotating streamwise vortices from the WLE and their evolution as an interface/buffer between the LSBs and the adjacent fully separated shear layers are discussed in detail. The current simulation results confirm that an increased lift and a decreased drag are achieved by using the WLEs compared to the straight leading edge (SLE) case, as observed in previous experiments. Additionally, the WLE cases exhibit a significantly reduced level of unsteady fluctuations in aerodynamic forces at the frequency of periodic vortex shedding. The beneficial aerodynamic characteristics of the WLE cases are attributed to the following three major events observed in the current simulations: (i) the appearance of a large low-pressure zone near the leading edge created by the LSBs; (ii) the reattachment of flow behind the LSBs resulting in a decreased volume of the rear wake; and, (iii) the deterioration of von-Kármán (periodic) vortex shedding due to the breakdown of spanwise coherent structures.

JFM classification

Flow Control: Flow Control Wakes/Jets: Separated flows Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 813 , 25 February 2017 , pp. 23 - 52
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cabral, B. & Leedom, L. C. 1993 Imaging vector fields using line integral convolution. In Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques, pp. 263–270. ACM.CrossRefGoogle Scholar
Custodio, D.2007 The effect of humpback whale-like leading edge protuberances on hydrofoil performance. Master of Science thesis, Worcester Polytechnic Institute.Google Scholar
Dropkin, A., Custodio, D., Henoch, C. W. & Johari, H. 2012 Computation of flow field around an airfoil with leading-edge protuberances. J. Aircraft 49 (5), 1345–1355.CrossRefGoogle Scholar
Favier, J., Pinelli, A. & Piomelli, U. 2012 Control of the separated flow around an airfoil using a wavy leading edge inspired by humpback whale flippers. C. R. Méc. 340 (1–2), 107–114.Google Scholar
Fish, F. E. & Battle, J. M. 1995 Hydrodynamic design of the humpback whale flipper. J. Morphol. 225 (1), 51–60.Google Scholar
Garmann, D. J., Visbal, M. R. & Orkwis, P. D. 2013 Comparative study of implicit and subgrid-scale model large-eddy simulation techniques for low-Reynolds number airfoil applications. Intl J. Numer. Meth. Heat Fluid Flow 71 (12), 1546–1565.Google Scholar
Georgiadis, N. J., Rizzetta, D. P. & Fureby, C. 2010 Large-eddy simulation: current capabilities, recommended practices, and future research. AIAA J. 48 (8), 1772–1784.Google Scholar
Guerreiro, J. L. E. & Sousa, J. M. M. 2012 Low-Reynolds-number effects in passive stall control using sinusoidal leading edges. AIAA J. 50 (2), 461–469.Google Scholar
Hansen, K. L., Kelso, R. M. & Dally, B. D. 2011 Performance variations of leading-edge tubercles for distinct airfoil profiles. AIAA J. 49, 185–194.Google Scholar
Hansen, K. L., Rostamzadeh, N., Kelso, R. M. & Dally, B. B. 2016 Evolution of the streamwise vortices generated between leading edge tubercles. J. Fluid Mech. 788, 730–766.Google Scholar
Jacobs, E. N.1932 The aerodynamic characteristics of eight very thick airfoils from tests in the variable density wind tunnel. NACA Tech. Rep. 391, pp. 545–556.Google Scholar
Johari, H., Henoch, C., Custodio, D. & Levshin, L. 2007 Effects of leading-edge protuberances on airfoil performance. AIAA J. 45, 2634–2642.Google Scholar
Kim, J. W. 2007 Optimised boundary compact finite difference schemes for computational aeroacoustics. J. Comput. Phys. 225, 995–1019.Google Scholar
Kim, J. W. 2010 High-order compact filters with variable cut-off wavenumber and stable boundary treatment. Comput. Fluids 39, 1168–1182.CrossRefGoogle Scholar
Kim, J. W. 2013 Quasi-disjoint pentadiagonal matrix systems for the parallelization of compact finite-difference schemes and filters. J. Comput. Phys. 241, 168–194.Google Scholar
Kim, J. W. & Haeri, S. 2015 An advanced synthetic eddy method for the computation of aerofoil–turbulence interaction noise. J. Comput. Phys. 287, 1–17.Google Scholar
Kim, J. W., Haeri, S. & Joseph, P. 2016 On the reduction of aerofoil–turbulence interaction noise associated with wavy leading edges. J. Fluid Mech. 792, 526–552.Google Scholar
Kim, J. W., Lau, A. S. H. & Sandham, N. D. 2010 Proposed boundary conditions for gust–airfoil interaction noise. AIAA J. 48 (11), 2705–2710.Google Scholar
Kim, J. W. & Lee, D. J. 2000 Generalized characteristic boundary conditions for computational aeroacoustics. AIAA J. 38 (11), 2040–2049.Google Scholar
Kim, J. W. & Lee, D. J. 2004 Generalized characteristic boundary conditions for computational aeroacoustics. Part 2. AIAA J. 42 (1), 47–55.Google Scholar
Kim, J. W. & Morris, P. J. 2002 Computation of subsonic inviscid flow past a cone using high-order schemes. AIAA J. 40 (10), 1961–1968.Google Scholar
Lau, A. S. H., Haeri, S. & Kim, J. W. 2013 The effect of wavy leading edges on aerofoil–gust interaction noise. J. Sound Vib. 25, 6234–6253.Google Scholar
Lienhard, J. H.1966 Synopsis of lift, drag, and vortex frequency data for rigid circular cylinders. Bulletin 300. Technical Extension Service, Washington State University, pp. 1–32.Google Scholar
Miklosovic, D. S., Murray, M. M. & Howle, L. E. 2007 Experimental evaluation of sinusoidal leading edges. J. Aircraft 44 (4), 1404–1408.Google Scholar
Miklosovic, D. S., Murray, M. M., Howle, L. E. & Fish, F. E. 2004 Leading-edge tubercles delay stall on humpback whale flippers. Phys. Fluids 16, 39–42.Google Scholar
Narayanan, S., Chaitanya, P., Haeri, S., Joseph, P., Kim, J. W. & Polacsek, C. 2015 Airfoil noise reductions through leading edge serrations. Phys. Fluids 27 (2), 025109.Google Scholar
Ozen, C. A. & Rockwell, D. 2010 Control of vortical structures on a flapping wing via a sinusoidal leading-edge. Phys. Fluids 22 (2), 021701.CrossRefGoogle Scholar
Pedro, H. T. C. & Kobayashi, M. H. 2008 Numerical study of stall delay on humpback whale flippers. In 46th AIAA Aerospace Sciences Meeting and Exhibit. AIAA.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19, 125–155.Google Scholar
Perry, A. E. & Hornung, H. C. 1984 Some aspects of three-dimensional separation. Part II: vortex skeletons. Z. Flugwiss. Weltraumforsch. 8, 155–160.Google Scholar
Rostamzadeh, N., Hansen, K. L., Kelso, R. M. & Dally, B. B. 2014 The formation mechanism and impact of streamwise vortices on NACA 0021 airfoil’s performance with undulating leading edge modification. Phys. Fluids 26 (10), 107101.Google Scholar
Skillen, A., Revell, A., Pinelli, A., Piomelli, U. & Favier, J. 2015 Flow over a wing with leading-edge undulations. AIAA J. 53 (2), 464–472.Google Scholar
Stack, J.1931 Tests in the variable density wind tunnel to investigate the effects of scale and turbulence on airfoil characteristics. Tech. Rep. National Advisory Committee for Aeronautics. Langley Aeronautical Lab.Google Scholar
Watmuff, J. H. 1999 Evolution of a wave packet into vortex loops in a laminar separation bubble. J. Fluid Mech. 397, 119–169.Google Scholar
Weber, P. W., Howle, L. E., Murray, M. M. & Miklosovic, D. S. 2011 Computational evaluation of the performance of lifting surfaces with leading-edge protuberances. J. Aircraft 48 (2), 591–600.CrossRefGoogle Scholar
Yarusevych, S., Sullivan, P. E. & Kawall, J. G. 2009 On vortex shedding from an airfoil in low-Reynolds-number flows. J. Fluid Mech. 632, 245–271.Google Scholar
Yoon, H. S., Hung, P. A., Jung, J. H. & Kim, M. C. 2011 Effect of the wavy leading edge on hydrodynamic characteristics for flow around low aspect ratio wing. Comput. Fluids 49, 276–289.Google Scholar
Zhang, M. M., Wang, G. F. & Xu, J. Z. 2013 Aerodynamic control of low-Reynolds-number airfoil with leading-edge protuberances. AIAA J. 51 (8), 1960–1971.Google Scholar