Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T11:25:01.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-eddy simulation of laminar transonic buffet

Published online by Cambridge University Press:  04 July 2018

Julien Dandois Open the ORCID record for Julien Dandois [Opens in a new window] ,
Ivan Mary  and
Vincent Brion
Julien Dandois*
Affiliation:
DAAA, ONERA, Université Paris Saclay, 8 rue des Vertugadins, 92190 Meudon, France
Ivan Mary
Affiliation:
DAAA, ONERA, Université Paris Saclay, 8 rue des Vertugadins, 92190 Meudon, France
Vincent Brion
Affiliation:
DAAA, ONERA, Université Paris Saclay, 8 rue des Vertugadins, 92190 Meudon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A large-eddy simulation of laminar transonic buffet on an airfoil at a Mach number 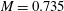$M=0.735$, an angle of attack 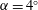$\unicode[STIX]{x1D6FC}=4^{\circ }$, a Reynolds number 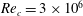$Re_{c}=3\times 10^{6}$ has been carried out. The boundary layer is laminar up to the shock foot and laminar/turbulent transition occurs in the separation bubble at the shock foot. Contrary to the turbulent case for which wall pressure spectra are characterised by well-marked peaks at low frequencies (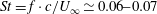$St=f\cdot c/U_{\infty }\simeq 0.06{-}0.07$, where 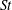$St$ is the Strouhal number, 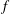$f$ the shock oscillation frequency, $c$ the chord length and 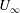$U_{\infty }$ the free-stream velocity), in the laminar case, there are also well-marked peaks but at a much higher frequency (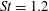$St=1.2$). The shock oscillation amplitude is also lower: 6 % of chord and limited to the shock foot area in the laminar case instead of 20 % with a whole shock oscillation and intermittent boundary layer separation and reattachment in the turbulent case. The analysis of the phase-averaged fields allowed linking of the frequency of the laminar transonic buffet to a separation bubble breathing phenomenon associated with a vortex shedding mechanism. These vortices are convected at 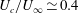$U_{c}/U_{\infty }\simeq 0.4$ (where 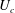$U_{c}$ is the convection velocity). The main finding of the present paper is that the higher frequency of the shock oscillation in the laminar regime is due to a different mechanism than in the turbulent one: laminar transonic buffet is due to a separation bubble breathing phenomenon occurring at the shock foot.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Shock waves Turbulent Flows: Turbulent transition
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 156 - 178
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agostini, L., Larchevêque, L., Dupont, P., Debiève, J. F. & Dussauge, J.-P. 2012 Zones of influence and shock motion in a shock/boundary-layer interaction. AIAA J. 50 (6), 1377–1387.Google Scholar
Alam, M. & Sandham, N. D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 410, 1–28.Google Scholar
Beneddine, S., Sipp, D., Arnault, A., Dandois, J. & Lesshafft, L. 2016 Conditions for validity of mean flow stability analysis. J. Fluid Mech. 798, 485–504.Google Scholar
Benoit, B. & Legrain, I.1987 Buffeting prediction for transport aircraft applications based on unsteady pressure measurement. In 5th AIAA Applied Aerodynamics Conference. AIAA Paper 87-2356.Google Scholar
Brion, V., Dandois, J., Abart, J.-C. & Paillart, P. 2017 Experimental analysis of the shock dynamics on a transonic laminar airfoil. EUCASS Prog. Flight Phys. 9, 365–386.Google Scholar
Bur, R., Brion, V. & Molton, P. 2014 An overview of recent experimental studies conducted in ONERA S3Ch transonic wind tunnel. In 29th Congress of the International Council of the Aeronautical Sciences, St Petersburg, Russia. ICAS.Google Scholar
Bur, R. & Garnier, E. 2016 Transition effect on a shock-wave/boundary layer interaction. In ECCOMAS Congress 2016, 5–10 June 2016, Crete Island, Greece. ECCOMAS.Google Scholar
Crouch, J. D., Garbaruk, A., Magidov, D. & Jacquin, L. 2009a Global structure of buffeting flow on transonic airfoils. In IUTAM Symposium on Unsteady Separated Flows and their Control, IUTAM Bookseries (ed. Braza, M. & Hourigan, K.), vol. 14, pp. 297–306. Springer.Google Scholar
Crouch, J. D., Garbaruk, A., Magidov, D. & Travin, A. 2009b Origin and structure of transonic buffet on airfoils. J. Fluid Mech. 628, 357–369.Google Scholar
Dandois, J., Garnier, E. & Sagaut, P. 2007 Numerical simulation of active separation control by a synthetic jet. J. Fluid Mech. 574, 25–58.Google Scholar
Davidson, T. S. & Babinsky, H.2016 Influence of transition on the flow downstream of normal shock wave-boundary layer interactions. In 54th AIAA Aerospace Sciences Meeting. AIAA Paper 2016-0044.Google Scholar
Dor, J. B., Mignosi, A., Seraudie, A. & Benoit, B. 1989 Wind tunnel studies of natural shock wave separation instabilities for transonic airfoil tests. In Symposium Transsonicum III, pp. 417–427. Springer.Google Scholar
Dupont, P., Haddad, C. & Debiève, J. F. 2006 Space and time organization in a shock induced boundary layer. J. Fluid Mech. 559, 255–277.Google Scholar
Dussauge, J.-P., Dupont, P. & Debiève, J.-F. 2006 Unsteadiness in shock wave boundary layer interactions with separation. Aerosol Sci. Technol. 10, 85–91.Google Scholar
Edwards, J. R. & Liou, M. S. 1998 Low-diffusion flux-splitting methods for flows at all speeds. AIAA J. 36, 1610–1617.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–394.Google Scholar
Hammond, D. A. & Redekopp, L. G. 1998 Local and global instability properties of separation bubbles. Eur. J. Mech. (B/Fluids) 17, 317–328.Google Scholar
Huerre, P. & Rossi, M. 1991 Stability of velocity profiles with reverse flow. In Instability, ICASE-Workshop, Berlin (ed. Hussaini, M. Y., Kumar, A. & Streett, C. L.). Springer.Google Scholar
Huerre, P. & Rossi, M. 1998 Hydrodynamic instabilities in open flows. In Hydrodynamics and Nonlinear Instabilities (ed. Godrèche, C. & Manneville, P.). Cambridge University Press.Google Scholar
Jacquin, L., Molton, P., Deck, S., Maury, B. & Soulevant, D. 2009 Experimental study of shock oscillation over a transonic supercritical profile. AIAA J. 47 (9), 1985–1994.Google Scholar
Kouchi, T., Yamaguchi, S., Koike, S., Nakajima, T., Sato, M., Kanda, H. & Yanase, S. 2016 Wavelet analysis of transonic buffet on a twodimensional airfoil with vortex generators. Exp. Fluids 57, 166.Google Scholar
Larchevêque, L.2016 Low- and medium- frequency unsteadinesses in a transitional shock–boundary reflection with separation. In 54th AIAA Aerospace Sciences Meeting. AIAA Paper 2016-1833.Google Scholar
Laurent, C., Mary, I., Gleize, V., Lerat, A. & Arnal, D. 2012 DNS database of a transitional separation bubble on a flat plate and application to rans modeling validation. Comput. Fluids 61, 21–30.Google Scholar
Lee, B. H. K. 1990 Oscillatory shock motion caused by transonic shock boundary-layer interaction. AIAA J. 28 (5), 942–945.Google Scholar
Lee, B. H. K. 2001 Self-sustained shock oscillations on airfoils at transonic speeds. Prog. Aerosp. Sci. 37 (2), 147–196.Google Scholar
Lee, B. H. K. & Tang, F. C.1988 An experimental study of transonic buffet of a supercritical airfoil with trailing edge flap. National Research Council of Canada, AN-54. NRC.Google Scholar
Mary, I. & Sagaut, P. 2002 LES of a flow around an airfoil near stall. AIAA J. 40, 1139–1145.Google Scholar
Marquillie, M. & Ehrenstein, U. 2003 On the onset of nonlinear oscillations in a separating boundary-layer flow. J. Fluid Mech. 490, 169–188.Google Scholar
McDevitt, J. B. & Okuno, A. F.1985 Static and dynamic pressure measurements on a NACA 0012 airfoil in the ames high Reynolds number facility. NASA TP-2485.Google Scholar
Memmolo, A., Bernardini, M. & Pirozzoli, S. 2016 Scrutiny of buffet mechanisms in transonic flow. In 51st 3AF International Conference on Applied Aerodynamics, Strasbourg, France. 3AF.Google Scholar
Owen, P. R. & Klanfer, L. 1953 On the laminar boundary layer separation from the leading edge of a thin aerofoil. In ARC Conf. Proc. 220. ARC.Google Scholar
Pearcey, H. H.1958 A method for the prediction of the onset of buffeting and other separation effects fromwind tunnel tests on rigid models. AGARD TR-223. AGARD.Google Scholar
Péchier, M., Guillen, P. & Gayzac, R. 2001 Magnus effect over finned projectiles. J. Spacecr. Rockets 38, 542–549.Google Scholar
Rist, U. 2004 Instability and transition mechanisms in laminar separation bubbles. In RTO-AVT-VKI Lecture Series. Von Karman Institute.Google Scholar
Sansica, A., Sandham, N. D. & Hu, Z. 2014 Forced response of a laminar shock-induced separation bubble. Phys. Fluids 26, 093601.Google Scholar
Sansica, A., Sandham, N. D. & Hu, Z. 2016 Instability and low-frequency unsteadiness in a shock-induced laminar separation bubble. J. Fluid Mech. 798, 5–26.Google Scholar
Sartor, F., Mettot, C. & Sipp, D. 2014 Stability, receptivity, and sensitivity analyses of buffeting transonic flow over a profile. AIAA J. 53 (7), 1980–1993.Google Scholar
Touber, E. & Sandham, N. D. 2011 Low-order stochastic modelling of low-frequency motions in reflected shock-wave/boundary-layer interaction. J. Fluid Mech. 671, 417–465.Google Scholar
Vreman, A. W.1995 Direct and large eddy simulation of the compressible turbulent mixing layer. PhD thesis, University of Twente.Google Scholar
Wu, M. & Martin, M. P. 2008 Analysis of shock motion in shockwave and turbulent boundary layer interaction using direct numerical simulation data. J. Fluid Mech. 594, 71–83.Google Scholar
Yang, Z. & Voke, P. R. 2001 Large-eddy simulation of boundary-layer separation and transition at a change of surface curvature. J. Fluid Mech. 439, 305–333.Google Scholar
Zhao, Z., Ren, X., Gao, C., Xiong, J., Liu, F. & Luo, S.2013 Experimental study of shock wave oscillation on SC(2)-0714 airfoil. In 51st AIAA Aerospace Sciences Meeting. AIAA 2013-0537.Google Scholar
Supplementary material: Image

Dandois et al. supplementary movie 1

Contour map of the streamwise velocity

Download Dandois et al. supplementary movie 1(Image)
Image 3.4 MB
Supplementary material: Image

Dandois et al. supplementary movie 2

Contour map of the normalised spectral mode of the streamwise velocity at the buffet frequency obtained by POD filtering

Download Dandois et al. supplementary movie 2(Image)
Image 3.3 MB