Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-06T12:09:26.723Z Has data issue: false hasContentIssue false
  • English
  • Français

Laminar–turbulent transition induced by a discrete roughness element in a supersonic boundary layer

Published online by Cambridge University Press:  29 October 2013

N. De Tullio Open the ORCID record for N. De Tullio [Opens in a new window] ,
P. Paredes ,
N. D. Sandham  and
V. Theofilis
N. De Tullio*
Affiliation:
Aeronautics and Astronautics, Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
P. Paredes
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, Plaza Cardenal Cisneros 3, E-28040 Madrid, Spain
N. D. Sandham
Affiliation:
Aeronautics and Astronautics, Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
V. Theofilis
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, Plaza Cardenal Cisneros 3, E-28040 Madrid, Spain
*
†Present address: Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear instability and breakdown to turbulence induced by an isolated roughness element in a boundary layer at Mach $2. 5$, over an isothermal flat plate with laminar adiabatic wall temperature, have been analysed by means of direct numerical simulations, aided by spatial BiGlobal and three-dimensional parabolized (PSE-3D) stability analyses. It is important to understand transition in this flow regime since the process can be slower than in incompressible flow and is crucial to prediction of local heat loads on next-generation flight vehicles. The results show that the roughness element, with a height of the order of the boundary layer displacement thickness, generates a highly unstable wake, which is composed of a low-velocity streak surrounded by a three-dimensional high-shear layer and is able to sustain the rapid growth of a number of instability modes. The most unstable of these modes are associated with varicose or sinuous deformations of the low-velocity streak; they are a consequence of the instability developing in the three-dimensional shear layer as a whole (the varicose mode) or in the lateral shear layers (the sinuous mode). The most unstable wake mode is of the varicose type and grows on average 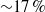${\sim }17\hspace{0.167em} \% $ faster than the most unstable sinuous mode and 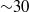${\sim }30$ times faster than the most unstable boundary layer mode occurring in the absence of a roughness element. Due to the high growth-rates registered in the presence of the roughness element, an amplification factor of 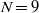$N= 9$ is reached within 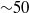${\sim }50$ roughness heights from the roughness trailing edge. The independently performed Navier–Stokes, spatial BiGlobal and PSE-3D stability results are in excellent agreement with each other, validating the use of simplified theories for roughness-induced transition involving wake instabilities. Following the linear stages of the laminar–turbulent transition process, the roll-up of the three-dimensional shear layer leads to the formation of a wedge of turbulence, which spreads laterally at a rate similar to that observed in the case of compressible turbulent spots for the same Mach number.

JFM classification

Compressible Flows: Compressible boundary layers Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 735 , 25 November 2013 , pp. 613 - 646
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfredsson, P. H. & Matsubara, M. 1996 Streaky structures in transition. In Transitional Boundary Layers in Aeronautics (ed. Henkes, R. & van Ingen, J.), pp. 374–386. Elsevier.Google Scholar
Amestoy, P. R., Duff, I. S., Koster, J. & L’Excellent, J.-Y. 2001 A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Applics 1, 15–41.CrossRefGoogle Scholar
Amestoy, P. R., Guermouche, A., L’Excellent, J.-Y. & Pralet, S. 2006 Hybrid scheduling for the parallel solution of linear systems. Parallel Comput. 2, 136–156.CrossRefGoogle Scholar
Andersson, P., Berggren, M. & Henningson, D. S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11 (1), 134–150.CrossRefGoogle Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. S. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.CrossRefGoogle Scholar
Asai, M., Minagawa, M. & Nishioka, M. 2002 The instability and breakdown of a near-wall low-speed streak. J. Fluid Mech. 455, 289–314.CrossRefGoogle Scholar
Balakumar, P. 2008 Boundary layer receptivity due to roughness and freestream sound for supersonic flows over axisymmetric cones. AIAA Paper 2008-4399.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2012 Compressibility effects on roughness-induced boundary layer transition. Intl J. Heat Fluid Flow 35, 45–51.CrossRefGoogle Scholar
Bertolotti, F. P. & Herbert, T. 1991 Analysis of the linear stability of compressible boundary layers using the PSE. Theor. Comput. Fluid Dyn. 3 (2), 117–124.CrossRefGoogle Scholar
Bertolotti, F. P., Herbert, T. & Spalart, P. 1992 Linear and nonlinear stability of the Blasius boundary layer. J. Fluid Mech. 242, 441–474.CrossRefGoogle Scholar
Bonfigli, G. & Kloker, M. 2007 Secondary instability of crossflow vortices: validation of the stability theory by direct numerical simulation. J. Fluid Mech. 583, 229–272.CrossRefGoogle Scholar
Brandt, L. & de Lange, H. C. 2008 Streak interactions and breakdown in boundary layer flows. Phys. Fluids 20, 024107.CrossRefGoogle Scholar
Bridges, T. J. & Morris, P. J. 1984 Differential eigenvalue problems in which the parameter appears nonlinearly. J. Comput. Phys. 55, 437–460.CrossRefGoogle Scholar
Broadhurst, M. & Sherwin, S. 2008 The parabolised stability equations for 3D-flows: implementation and numerical stability. Appl. Numer. Maths 58 (7), 1017–1029.CrossRefGoogle Scholar
Broadhurst, M., Theofilis, V. & Sherwin, S. 2006 Spectral element stability analysis of vortical flows. In IUTAM Symposium on Laminar–Turbulent Transition (ed. Govindarajan, R.), pp. 153–158. Springer.CrossRefGoogle Scholar
Carpenter, M. H., Nordstrom, J. & Gottlieb, D. 1999 A stable and conservative interface treatment of arbitrary spatial accuracy. J. Comput. Phys. 148, 341–365.CrossRefGoogle Scholar
Chang, C. L., Malik, M. R., Erlebacher, G. & Hussaini, M. Y. 1991 Compressible stability of growing boundary layers using parabolized stability equations. AIAA Paper 91-1636.CrossRefGoogle Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2 (5), 765–777.CrossRefGoogle Scholar
Choudhari, M., Li, F., Chang, C. L., Norris, A. & Edwards, J. 2013 Wake instabilities behind discrete roughness elements in high speed boundary layers. AIAA Paper 2013-0081.CrossRefGoogle Scholar
Choudhari, M., Li, F., Minwei, W., Chang, C. L. & Edwards, J. 2010 Laminar–turbulent transition behind discrete roughness elements in a high-speed boundary layer. AIAA Paper 2010-1575.CrossRefGoogle Scholar
Choudhari, M. & Street, C. L. 1992 A finite Reynolds-number approach for the prediction of boundary-layer receptivity in localized regions. Phys. Fluids A 4 (11), 2495–2514.CrossRefGoogle Scholar
Corke, T. C., Bar-Server, A. & Morkovin, M. V. 1986 Experiments on transition enhancement by distributed roughness. Phys. Fluids 29 (10), 3199–3213.CrossRefGoogle Scholar
Crouch, J. D. 1992 Localized receptivity of boundary layers. Phys. Fluids A 4 (7), 1408–1414.CrossRefGoogle Scholar
De Tullio, N. & Sandham, N. D. 2010 Direct numerical simulation of breakdown to turbulence in a Mach 6 boundary layer over a porous surface. Phys. Fluids 22, 094105.CrossRefGoogle Scholar
De Tullio, N. & Sandham, N. D. 2012 Direct numerical simulations of roughness receptivity and transitional shock-wave/boundary-layer interactions. RTO-MP-AVT-200. Art. 22, NATO.Google Scholar
Eckert, E. R. G. 1955 Engineering relations for friction and heat transfer to surfaces in high velocity flow. J. Aero. Sci. 22 (8), 585–587.Google Scholar
Fiala, A., Hillier, R., Mallinson, S. G. & Wijesinghe, H. S. 2006 Heat transfer measurement of turbulent spots in a hypersonic blunt-body boundary layer. J. Fluid Mech. 555, 81–111.CrossRefGoogle Scholar
Fischer, M. C. 1972 Spreading of a turbulent disturbance. AIAA J. 10 (7), 957–959.CrossRefGoogle Scholar
Fujii, K. 2006 Experiment of the two-dimensional roughness effect on hypersonic boundary-layer transition. J. Spacecr. Rockets 43 (4), 731–738.CrossRefGoogle Scholar
Galionis, I. & Hall, P. 2005 Spatial stability of the incompressible corner flow. Theor. Comp. Fluid Dyn. 19, 77–113.CrossRefGoogle Scholar
Gaster, M., Grosch, C. E. & Jackson, T. L. 1994 The velocity field created by a shallow bump in a boundary layer. Phys. Fluids 6 (9), 3079–3085.CrossRefGoogle Scholar
Goldstein, M. E. 1985 Scattering of acoustic waves into Tollmien–Schlichting waves by small streamwise variations in surface geometry. J. Fluid Mech. 154, 509–529.CrossRefGoogle Scholar
Groskopf, G., Kloker, M. J. & Marxen, O. 2009 Bi-global crossplane stability analysis of high-speed boundary-layer flows with discrete roughness. In IUTAM Symposium on Laminar–Turbulent Transition (ed. Henningson, D. & Schlatter, P.), pp. 171–176. Springer.Google Scholar
Herbert, T. 1994 Parabolized stability equations. AGARD Rep. 793. Special Course on Progress in Transition Modelling, pp. 4(1)–4(34).Google Scholar
Herbert, T. 1997 Parabolized stability equations. Annu. Rev. Fluid Mech. 29, 245–283.CrossRefGoogle Scholar
Hermanns, M. & Hernández, J. A. 2008 Stable high-order finite-difference methods based on non-uniform grid point distributions. Intl J. Numer. Meth. Fluids 56, 233–255.CrossRefGoogle Scholar
Horvath, T. J., Berri, S. A. & Merski, N. R. 2004 Hypersonic boundary/shear layer transition for blunt to slender configurations: a NASA Langley experimental perspective. Tech. Rep. RTO-MP-AVT-111 (22), NATO.Google Scholar
Hultgren, L. S. & Gustavsson, H. 1981 Algebraic growth of disturbances in a laminar boundary layer. Phys. Fluids 24, 1000.CrossRefGoogle Scholar
Jacobs, R. G. & Durbin, P. A. 2001 Simulations of bypass transition. J. Fluid Mech. 428, 185–212.CrossRefGoogle Scholar
Jones, L. E. 2008 Numerical study of the flow around an airfoil at low Reynolds number. PhD thesis, School of Engineering Sciences, University of Southampton.Google Scholar
Joslin, R. D. & Grosch, C. E. 1995 Growth characteristics downstream of a shallow bump: computation and experiment. Phys. Fluids 7 (12), 3042–3047.CrossRefGoogle Scholar
Kegerise, M., King, R., Owens, L., Choudhari, M., Li, F., Chang, C. L. & Norris, A. 2012 An experimental and numerical study of roughness-induced instabilities in a Mach 3.5 boundary layer. RTO-MP-AVT-200. Art. 29, NATO.Google Scholar
Kegerise, M. A., Owens, L. R. & Rudolf, A. K. 2010 High-speed boundary-layer transition induced by an isolated roughness element. AIAA Paper 2010-4999.CrossRefGoogle Scholar
Klebanoff, P. S. & Tidstrom, K. D. 1972 Mechanism by which a two-dimensional roughness element induces boundary layer transition. Phys. Fluids 15 (7), 1173–1188.CrossRefGoogle Scholar
Krishnan, L. & Sandham, N. D. 2006 Effect of Mach number on the structure of turbulent spots. J. Fluid Mech. 566, 225–234.CrossRefGoogle Scholar
Landahl, M. T. 1975 Wave breakdown and turbulence. SIAM J. Appl. Maths 28 (4), 735–756.CrossRefGoogle Scholar
Li, F. & Malik, M. R. 1997 Spectral analysis of parabolized stability equations. Comput. Fluids 26 (3), 279–297.CrossRefGoogle Scholar
Li, Q. 2003 Numerical study of the Mach number effect in compressible wall-bounded turbulence. PhD thesis, School of Engineering Sciences, University of Southampton.Google Scholar
Mack, L. M. 1969 Boundary layer stability theory. JPL Report 900-277, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, USA.Google Scholar
Marxen, O., Iaccarino, G. & Shaqfeh, S. G. 2010 Disturbance evolution in a Mach 4.8 boundary layer with two-dimensional roughness-induced separation and shock. J. Fluid Mech. 648, 435–469.CrossRefGoogle Scholar
Mughal, M. S. 2006 Stability analysis of complex wing geometries: parabolised stability equations in generalized non-orthogonal coordinates. AIAA Paper 2006-3222.CrossRefGoogle Scholar
Muppidi, S. & Mahesh, K. 2012 Direct numerical simulations of roughness-induced transition in supersonic boundary layers. J. Fluid Mech. 693, 28–56.CrossRefGoogle Scholar
Owens, L. R., Kegerise, M. A. & Wilkinson, S. P. 2011 Off-body boundary-layer measurement techniques development for supersonic low-disturbance flows. AIAA Paper 2011-0284.CrossRefGoogle Scholar
Paredes, P., Hermanns, M., Le Clainche, S. & Theofilis, V. 2013 Order 104 speedup in global linear instability analysis using matrix formation. Comput. Meth. Appl. Mech. Engng 253, 287–304.CrossRefGoogle Scholar
Paredes, P., Theofilis, V., Rodríguez, D. & Tendero, J. A. 2011 The PSE-3D instability analysis methodology for flows depending strongly on two and weakly on the third spatial dimension. AIAA Paper 2011-3752.CrossRefGoogle Scholar
Pirozzoli, S., Grasso, F. & Gatski, T. B. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at $M= 2. 5$ . Phys. Fluids 16 (3), 530–545.CrossRefGoogle Scholar
Reda, D. C. 2002 Review and synthesis of roughness-dominated transition correlations for reentry vehicles. J. Spacecr. Rockets 39 (2), 161–167.CrossRefGoogle Scholar
Reddy, S. C., Schmid, P. J., Baggett, J. S. & Henningson, D. S. 2001 Simulations of bypass transition. J. Fluid Mech. 428, 185–212.Google Scholar
Redford, J. A., Sandham, N. D. & Roberts, G. T. 2010 Compressibility effects on boundary-layer transition induced by an isolated roughness element. AIAA J. 48 (12), 2818–2830.CrossRefGoogle Scholar
Redford, J. A., Sandham, N. D. & Roberts, G. T. 2012 Numerical simulations of turbulent spots in supersonic boundary layers: effects of Mach number and wall temperature. Prog. Aerosp. Sci. 52, 67–79.CrossRefGoogle Scholar
Reshotko, E. 2001 Transient growth: a factor in bypass transition. Phys. Fluids 13 (5), 1067–1075.CrossRefGoogle Scholar
Reshotko, E. & Tumin, A. 2004 Role of transient growth on roughness-induced transition. AIAA J. 42 (4), 766–770.CrossRefGoogle Scholar
Rizzetta, D. P. & Visbal, M. R. 2007 Direct numerical simulations of flow past an array of distributed roughness elements. AIAA J. 45 (8), 1967–1976.CrossRefGoogle Scholar
Ruban, A. I. 1984 On Tollmien–Schlichting wave generation by sound. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 5, 44–52.Google Scholar
Saad, Y. 1980 Variations of Arnoldi’s method for computing eigenelements of large unsymmetric matrices. Linear Algebr. Applics. 34, 269–295.CrossRefGoogle Scholar
Saad, Y. 1994 SPARSKIT: a basic tool kit for sparse matrix computations, version 2, http://www-users.cs.umn.edu/~saad/software/SPARSKIT/index.html.Google Scholar
Sandham, N. D., Li, Q. & Yee, H. C. 2002 Entropy splitting for high-order numerical simulation of compressible turbulence. J. Comput. Phys. 178, 307–322.CrossRefGoogle Scholar
Schneider, S. P. 2008 Effects of roughness on hypersonic boundary-layer transition. J. Spacecr. Rockets 45 (2), 193–209.CrossRefGoogle Scholar
Smith, A. M. O. & Gamberoni, N. 1956 Transition, pressure gradient and stability theory. Rep. ES-26388, Douglas Aircraft Co., El Segundo, California.Google Scholar
Swearingen, J. D. & Blackwelder, R. F. 1987 The growth and breakdown of streamwise vortices in the presence of a wall. J. Fluid Mech. 182, 255–290.CrossRefGoogle Scholar
Tani, I. & Sato, H. 1956 Boundary-layer transition by roughness element. J. Phys. Soc. Japan 11 (12), 1284–1291.CrossRefGoogle Scholar
Theofilis, V. 1995 Spatial stability of incompressible attachment-line flow. Theor. Comp. Fluid Dyn. 7 (3), 159–171.CrossRefGoogle Scholar
Theofilis, V. 2003 Advances in global linear instability of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 39 (4), 249–315.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.CrossRefGoogle Scholar
Thomson, K. W. 1987 Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 68, 1–24.CrossRefGoogle Scholar
Thomson, K. W. 1990 Time-dependent boundary conditions for hyperbolic systems. Part 2. J. Comput. Phys. 89, 439–461.CrossRefGoogle Scholar
Tumin, A. & Reshotko, E. 2005 Receptivity of a boundary-layer flow to a three-dimensional hump at finite Reynolds numbers. Phys. Fluids 17, 094101.CrossRefGoogle Scholar
Van Ingen, J. L. 1956 A suggested semi-empirical method for the calculation of boundary layer transition region. Rep. UTH-74, Department of Aerospace Engineering, Delft University of Technology.Google Scholar
Welch, P. D. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time-averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. AU-15, 70–73.CrossRefGoogle Scholar
Wheaton, B. M. & Schneider, S. P. 2012 Roughness-induced instability in a hypersonic laminar boundary layer. AIAA J. 5 (6), 1245–1256.CrossRefGoogle Scholar
Wheaton, B. M. & Schneider, S. P. 2013 Instability and transition due to near-critical roughness in a hypersonic laminar boundary layer. AIAA Paper 2013-0084.CrossRefGoogle Scholar
White, F. M 2005 Viscous Fluid Flow, 3rd edn. McGraw-Hill.Google Scholar
Wilkinson, J. H. 1965 The Algebraic Eigenvalue Problem. Clarendon.Google Scholar
Wray, A. A. 1990 Minimal storage time advancement schemes for spectral methods. Rep. M.S. 202 A-1, NASA Ames Research Centre.Google Scholar
Wu, X. & Choudhari, M. 2003 Linear and nonlinear instabilities of a Blasius boundary layer perturbed by streamwise vortices. Part 2. Intermittent instability induced by long-wavelength Klebanoff modes. J. Fluid Mech. 483, 249–286.CrossRefGoogle Scholar
Yao, Y., Shang, Z., Castagna, J., Johnstone, R., Jones, L. E., Redford, J. A., Sandberg, R. D., Sandham, N. D., Suponitsky, V. & De Tullio, N. 2009 Re-engineering a DNS code for high-performance computation of turbulent flows. AIAA Paper 2009-566.CrossRefGoogle Scholar