Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-06T10:38:48.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Laminar-to-turbulent transition of pipe flows through puffs and slugs

Published online by Cambridge University Press:  16 October 2008

MINA NISHI ,
BÜLENT ÜNSAL ,
FRANZ DURST  and
GAUTAM BISWAS
MINA NISHI
Affiliation:
Institute of Fluid Mechanics, Friedrich–Alexander Universität Erlangen–Nürnberg, Cauerstrasse 4, D–91058 Erlangen, [email protected]
BÜLENT ÜNSAL
Affiliation:
Institute of Fluid Mechanics, Friedrich–Alexander Universität Erlangen–Nürnberg, Cauerstrasse 4, D–91058 Erlangen, [email protected]
FRANZ DURST
Affiliation:
Institute of Fluid Mechanics, Friedrich–Alexander Universität Erlangen–Nürnberg, Cauerstrasse 4, D–91058 Erlangen, [email protected]
GAUTAM BISWAS
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Kanpur, Kanpur – 208016, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Laminar-to-turbulent transition of pipe flows occurs, for sufficiently high Reynolds numbers, in the form of slugs. These are initiated by disturbances in the entrance region of a pipe flow, and grow in length in the axial direction as they move downstream. Sequences of slugs merge at some distance from the pipe inlet to finally form the state of fully developed turbulent pipe flow. This formation process is generally known, but the randomness in time of naturally occurring slug formation does not permit detailed study of slug flows. For this reason, a special test facility was developed and built for detailed investigation of deterministically generated slugs in pipe flows. It is also employed to generate the puff flows at lower Reynolds numbers. The results reveal a high degree of reproducibility with which the triggering device is able to produce puffs. With increasing Reynolds number, ‘puff splitting’ is observed and the split puffs develop into slugs. Thereafter, the laminar-to-turbulent transition occurs in the same way as found for slug flows. The ring-type obstacle height, h, required to trigger fully developed laminar flows to form first slugs or puffs is determined to show its dependence on the Reynolds number, Re = DU/ν (where D is the pipe diameter, U is the mean velocity in the axial direction and ν is the kinematic viscosity of the fluid). When correctly normalized, h+ turns out to be independent of Reτ (where h+ = hUτ/ν, Reτ = DUτ/ν and 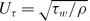; τw is the wall shear stress and ρ is the density of the fluid).

Type
Papers
Information
Journal of Fluid Mechanics , Volume 614 , 10 November 2008 , pp. 425 - 446
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bandyopadhyay, P. R. 1986 Aspects of equilibrium puff in transitional pipe flow. J. Fluid Mech. 163, 439–458.CrossRefGoogle Scholar
Darbyshire, A. G. & Mullin, T. 1995 Transition to turbulence in constant-mass-flux pipe flow. J. Fluid Mech. 289, 83–114.Google Scholar
Draad, A. A., Kuiken, G. & Nieuwstadt, F. T. M. 1998 Laminar-turbulent transition in pipe flow for newtonian and non-newtonian fluids. J. Fluid Mech. 377, 267–312.CrossRefGoogle Scholar
Durst, F., Heim, U., Ünsal, B. & Kullik, G. 2003 Mass flow rate control system for time–dependent laminar and turbulent flow investigations. Meas. Sci. Technol. 14, 893–902.Google Scholar
Durst, F., Ray, S., Unsal, B. & Bayoumi, O. A. 2005 The development lengths of laminar pipe and channel flows. J. Fluids Engng 127, 1154–1160.CrossRefGoogle Scholar
Durst, F. & Ünsal, B. 2006 Forced laminar to turbulent transition of pipe flows. J. Fluid Mech. 560, 449–464.CrossRefGoogle Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulent transition pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.CrossRefGoogle Scholar
Faisst, H. & Eckhardt, B. 2004 Sensitive dependence on initial conditions in transition to turbulence in pipe flow. J. Fluid Mech. 504, 343–352.Google Scholar
Hof, B., Juel, A. & Mullin, T. 2003 Scaling of the turbulence transition threshold in a pipe. Phys. Rev. Lett. 91, 244502, 1–4.Google Scholar
Jovanović, J. & Pashtrapanska, M. 2004 On the criterion for the determination transition onset and breakdown to turbulence in wall-bounded flows. J. Fluids Engng 126, 626–633.CrossRefGoogle Scholar
Kerswell, R. R. 2005 Recent progress in understanding the transition to turbulent in a pipe. Nonlinearity 18, R17–R44.Google Scholar
Lindgren, E. R. 1969 Propagation velocity of turbulent slugs and streaks in transition pipe flow. Phys. Fluids 12, 418–425.CrossRefGoogle Scholar
Mullin, T. & Peixinho, J. 2006 Transition to turbulence in pipe flow. J. Low. Temp. Phys. 145, 75–89.CrossRefGoogle Scholar
Peixinho, J. & Mullin, T. 2006 Decay of turbulence in pipe flow. Phys. Rev. Lett. 96, 094501. 1–4.Google Scholar
Peixinho, J. & Mullin, T. 2007 Finite-amplitude threshoulds for transition in pipe flow. J. Fluid Mech. 582, 169–178.CrossRefGoogle Scholar
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct of sinuous, and the law of resistance in parallel channels. Philos. Trans. R. Soc. Lond. A 174, 935–982.Google Scholar
Rotta, J. 1956 Experimenteller beitrag zur entstehung turbulenter strömung im rohr. Ing-Arch. 24, 258–281.CrossRefGoogle Scholar
Rubin, Y., Wygnanski, I. J. & Haritonidis, J. H. 1980 Further observations on transition in pipe. In Proc. IUTAM Symp. Stuttgart, FRG, pp. 19–26. Springer.Google Scholar
Trefethen, L., Chapman, S., Henningson, D., Meseguer, A., Mullin, T. & Nieuwstadt, F. 2000 Threshold amplitudes for transition to turbulence in a pipe. !http://arXiv.org/abs/physics/0007092.Google Scholar
Van Doorne, C. W. H., Hof, B., Nieuwstadt, F. T. M., Westerweel, J. & Wieneke, B. 2007 Investigation of turbulent puffs in pipe flow with time-resolved stereoscopic PIV. Exps. Fluids 42, 259–279.CrossRefGoogle Scholar
Willis, A. P. & Kerswell, R. R. 2007 Critical behavior in the relaminarization of localized turbulence in pipe flow. Phys. Rev. Lett. 98, 014501, 1–4.Google Scholar
Wygnanski, I. J. & Champagne, F. H. 1973 On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59, 281–351.CrossRefGoogle Scholar
Wygnanski, I. J., Sokolov, M. & Friedman, D. 1975 On transition in a pipe. Part 2. The equilibrium puff. J. Fluid Mech. 69, 283–304.Google Scholar