Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T06:45:08.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Laminarization mechanisms and extreme-amplitude states in rapidly rotating plane channel flow

Published online by Cambridge University Press:  30 July 2013

Stefan Wallin ,
Olof Grundestam  and
Arne V. Johansson
Stefan Wallin*
Affiliation:
Information and Aeronautical Systems, Swedish Defence Research Agency (FOI), SE-164 90 Stockholm, Sweden Linné Flow Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
Olof Grundestam
Affiliation:
Information and Aeronautical Systems, Swedish Defence Research Agency (FOI), SE-164 90 Stockholm, Sweden Linné Flow Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
Arne V. Johansson
Affiliation:
Linné Flow Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

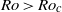Fully developed plane channel flow rotating in the spanwise direction has been studied analytically and numerically. Linear stability analysis reveals that all cross-flow modes are stable for supercritical rotation numbers, $Ro\gt R{o}_{c} $, where $R{o}_{c} $ will approach 3 from below for increasing Reynolds number. Plane Tollmien–Schlichting (TS) waves are independent of rotation and always linearly unstable for supercritical Reynolds numbers. Direct numerical simulation (DNS) of the laminarization process reveals that the turbulence is damped when 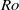$Ro$ approaches 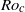$R{o}_{c} $. Hence, the laminarization is dominated by linear mechanisms. The flow becomes periodic for supercritical Reynolds numbers and rotation rates, i.e. when 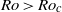$Ro\gt R{o}_{c} $ and 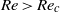$Re\gt R{e}_{c} $. At such rotation rates, all oblique (cross-flow) modes are damped and when the disturbance amplitude becomes small enough, the TS modes start to grow exponentially. Secondary instabilities are initially blocked by the rotation since all cross-flow modes are linearly stable and the breakdown to turbulence will be strongly delayed. Hence, the TS waves will reach extremely high amplitudes, much higher than for typical turbulent fluctuations. Eventually, the extreme-amplitude state with TS-like waves will break down to turbulence and the flow will laminarize due to the influence of the rapid rotation, thus completing the cycle that will then be repeated. This flow is strongly dominated by linear mechanisms, which is remarkable considering the extremely high amplitudes involved in the processes of laminarization of the turbulence at 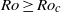$Ro\geq R{o}_{c} $ and the growth of the unstable TS waves.

JFM classification

Instability: Instability Turbulent Flows: Rotating turbulence Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 193 - 219
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfredsson, P. H. & Persson, H. 1989 Instabilities in channel flow with system rotation. J. Fluid Mech. 202, 543–557.Google Scholar
Bagheri, S. & Hanifi, A. 2007 The stabilizing effect of streaks on Tollmien–Schlichting and oblique waves: a parametric study. Phys. Fluids 19, 078103.Google Scholar
Bardina, J., Ferziger, J. H. & Reynolds, W. C. 1983 Improved turbulence models based on large-eddy simulation of homogeneous incompressible turbulent flows. Stanford University Tech. Rep. TF-19.Google Scholar
Bech, K. H. & Andersson, H. I. 1997 Turbulent plane Couette flow subject to strong system rotation. J. Fluid Mech. 347, 289–314.Google Scholar
Bradshaw, P. 1969 The analogy between streamline curvature and buoyancy in turbulent shear flow. J. Fluid Mech. 36, 177–191.Google Scholar
Brethouwer, G. 2005 The effect of rotation on rapidly sheared homogeneous turbulence and passive scalar transport. Linear theory and direct numerical simulation. J. Fluid Mech. 542, 305–342.Google Scholar
Brethouwer, G., Duguet, Y. & Schlatter, P. 2012 Turbulent-laminar coexistence in wall flows with Coriolis, buoyancy or Lorentz forces. J. Fluid Mech. 704, 137–172.Google Scholar
Brethouwer, G., Schlatter, P. & Johansson, A. V. 2011 Turbulence, instabilities and passive scalars in rotating channel flow. J. Phys.: Conf. Ser. 318, 032025.Google Scholar
Fransson, J. H. M., Brandt, L., Talamelli, A. & Cossu, C. 2005 Experimental study of the stabilization of Tollmien–Schlichting waves by finite amplitude streaks. Phys. Fluids 17, 054110.CrossRefGoogle Scholar
Grundestam, O., Wallin, S. & Johansson, A. V. 2008 Direct numerical simulations of rotating turbulent channel flow. J. Fluid Mech. 177–199.Google Scholar
Hamba, F. 2006 The mechanism of zero mean absolute vorticity state in rotating channel flow. Phys. Fluids 18, 125104.Google Scholar
Henningson, D. S., Lundbladh, A. & Johansson, A. V. 1993 A mechanism for bypass transition from localized disturbances in wall-bounded shear flows. J. Fluid Mech. 250, 169–207.Google Scholar
Jimenez, J. 1990 Transition to turbulence in two-dimensional Poiseuille flow. J. Fluid Mech. 218, 265–297.Google Scholar
Johnston, J. P., Halleen, R. M. & Lezius, D. K. 1972 Effects of spanwise system rotation on the structure of two-dimensional fully developed turbulent channel flow. J. Fluid Mech. 56, 533–559.Google Scholar
Krasnov, D., Rossi, M., Zikanov, O. & Boeck, T. 2008 Optimal growth and transition to turbulence in channel flow with spanwise magnetic field. J. Fluid Mech. 596, 73–101.Google Scholar
Kristoffersen, R. & Andersson, H. I. 1993 Direct simulations of low-Reynolds number turbulent flow in a rotating channel. J. Fluid Mech. 256, 163–197.Google Scholar
Lakin, W. D., Ng, B. S. & Reid, W. H. 1978 Approximations to the eigenvalue relation for the Orr–Sommerfeld problem. Phil. Trans. R. Soc. Lond. A 289, 347.Google Scholar
Lamballais, E., Lesieur, M. & Métais, O. 1996 Effects of spanwise rotation on the vorticity stretching in transitional and turbulent channel flow. Intl. J. Heat Fluid Flow 17, 324–332.Google Scholar
Lezius, D. K. & Johnston, J. P. 1976 Roll-cell instabilities in rotating laminar and turbulent channel flows. J. Fluid Mech. 77, 153–175.Google Scholar
Lin, C. C. 1955 The Theory of Hydrodynamic Stability. Cambridge University Press.Google Scholar
Lundblad, A., Henningson, D. S. & Johansson, A. V. 1992 An efficient spectral integration method for the solution of the Navier–Stokes equations. Tech. Rep. FOI, FFA, SE-16490, Stockholm, Sweden, 1992-28.Google Scholar
Nagata, M. 1998 Tertiary solutions and their stability in rotating plane Couette flow. J. Fluid Mech. 358, 357–378.Google Scholar
Nakabashi, K. & Kitoh, O. 1996 Low Reynolds number fully developed two-dimensional turbulent channel flow with system rotation. J. Fluid Mech. 315, 1–29.Google Scholar
Orszag, S. A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 659–703.Google Scholar
Salhi, A. & Cambon, C. 1997 An analysis of rotating shear flow using linear theory and dns and les results. J. Fluid Mech. 347, 171–195.Google Scholar
Tanaka, M., Kida, S., Yanase, S. & Kawahara, G. 2000 Zero-absolute-vorticity state in a rotating turbulent shear flow. Phys. Fluids 12 (8), 1979–1985.Google Scholar
Tsukahara, T., Tillmark, N. & Alfredsson, P. H. 2010 Flow regimes in a plane Couette flow with system rotation. J. Fluid Mech. 648, 5–33.CrossRefGoogle Scholar
Wall, D. P. & Nagata, M. 2006 Nonlinear secondary flow through a rotating channel. J. Fluid Mech. 564, 25–55.Google Scholar
Weideman, J. A. C & Reddy, S. C. 2000 A MATLAB differentiation matrix suite. ACM Trans. Math. Softw. 26 (4), 465–519.Google Scholar
Wu, H. & Kasagi, N. 2004 Effects of arbitrary directional system rotation on turbulent channel flow. Phys. Fluids 16 (4), 979–990.Google Scholar
Yanase, S., Tanaka, M., Kida, S. & Kawahara, G. 2004 Generation and sustenance mechanisms of coherent vortical structures in rotating shear turbulence of zero-mean-absolute vorticity. Fluid Dyn. Res. 35, 237–254.Google Scholar