Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T05:51:10.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Laminar separation bubble development on an airfoil emitting tonal noise

Published online by Cambridge University Press:  02 September 2015

S. Pröbsting  and
S. Yarusevych
S. Pröbsting
Affiliation:
Department of Aerodynamics, Wind Energy, Flight Performance, and Propulsion, Delft University of Technology, Delft 2629HS, The Netherlands
S. Yarusevych*
Affiliation:
Department of Mechanical and Mechatronics Engineering, University of Waterloo, Waterloo, N2L 3G1, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The subject of this experimental study is the feedback effects due to tonal noise emission in a laminar separation bubble (LSB) formed on the suction side of an airfoil in low Reynolds number flows. Experiments were performed on a NACA 0012 airfoil for a range of chord-based Reynolds numbers 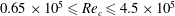$0.65\times 10^{5}\leqslant \mathit{Re}_{c}\leqslant 4.5\times 10^{5}$ at angle of attack 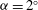${\it\alpha}=2^{\circ }$, where laminar boundary layer separation is encountered on both sides of the airfoil. Simultaneous time-resolved, two-component particle image velocimetry (PIV) measurements, unsteady surface pressure and far-field acoustic pressure measurements were employed to characterize flow development and acoustic emissions. Amplification of disturbances in separated shear layers on both the suction and pressure sides of the airfoil leads to shear layer roll-up and shedding of vortices from separation bubbles. When the vortices do not break up upstream of the trailing edge, the passage of these structures over the trailing edge generates tonal noise. Acoustic feedback between the trailing edge noise source and the upstream separation bubble narrows the frequency band of amplified disturbances, effectively locking onto a particular frequency. Acoustic excitation further results in notable changes to the overall separation bubble characteristics. Roll-up vortices forming on the pressure side, where the bubble is located closer to the trailing edge, are shown to define the characteristic frequency of pressure fluctuations, thereby affecting the disturbance spectrum on the suction side. However, when the bubble on the pressure side is suppressed via boundary layer tripping, a weaker feedback effect is also observed on the suction side. The results give a detailed quantitative description of the observed phenomenon and provide a new outlook on the role of coherent structures in separation bubble dynamics and trailing edge noise generation.

JFM classification

Acoustics: Aeroacoustics Boundary Layers: Boundary layer separation Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 780 , 10 October 2015 , pp. 167 - 191
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. & Sandham, N. D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 410, 223–250.CrossRefGoogle Scholar
Amiet, R. K. 1976 Noise due to turbulent flow past a trailing edge. J. Sound Vib. 47 (3), 387–393.Google Scholar
Arbey, H. & Bataille, J. 1983 Noise generated by airfoil profiles placed in a uniform laminar flow. J. Fluid Mech. 134, 33–47.Google Scholar
Arcondoulis, E. J. G., Doolan, C. J. & Zander, A. C. 2009 Airfoil noise measurements at various angles of attack and low Reynolds number. In Proceedings of ACOUSTICS 2009, Adelaide, Australia, 23–25 November. Australian Acoustical Society.Google Scholar
Arcondoulis, E. J. G., Doolan, C. J., Zander, A. C. & Brooks, L. A. 2013 An experimental investigation of airfoil tonal noise caused by an acoustic feedback loop. In Proceedings of ACOUSTICS 2013, Victor Harbor, Australia, 17–20 November. Australian Acoustical Society.Google Scholar
Atassi, H. M.1984 Feedback in separated flows over symmetric airfoils. Tech. Rep. TM-83758. AGARD.Google Scholar
Boutilier, M. S. H. & Yarusevych, S. 2012a Effects of end plates and blockage on low-Reynolds-number flows over airfoils. AIAA J. 50 (7), 1547–1559.Google Scholar
Boutilier, M. S. H. & Yarusevych, S. 2012b Parametric study of separation and transition characteristics over an airfoil at low Reynolds numbers. Exp. Fluids 52, 1491–1506.Google Scholar
Boutilier, M. S. H. & Yarusevych, S. 2012c Separated shear layer transition over an airfoil at a low Reynolds number. Phys. Fluids 24, 084105.Google Scholar
Brinkerhoff, J. R. & Yaras, M. I. 2011 Interaction of viscous and inviscid instability modes in separation-bubble transition. Phys. Fluids 23, 124102.CrossRefGoogle Scholar
Brooks, T. F., Marcolini, M. A. & Pope, D. S. 1986 Airfoil trailing-edge flow measurements. AIAA J. 24 (8), 1245–1251.Google Scholar
Burgmann, S., Brücker, C. & Schröder, W. 2006 Scanning PIV measurements of a laminar separation bubble. Exp. Fluids 41, 319–326.Google Scholar
Burgmann, S. & Schröder, W. 2008 Investigation of the vortex induced unsteadiness of a separation bubble via time-resolved and scanning PIV measurements. Exp. Fluids 45, 675–691.Google Scholar
Carmichael, B. H.1981 Low Reynolds number airfoil survey. NASA Tech. Rep. Contract Report No. 165803, Vol. I.Google Scholar
Chong, T. P. & Joseph, P. F. 2012 ‘Ladder’ structure in tonal noise generated by laminar flow around an airfoil. J. Acoust. Soc. Am. 131 (6), EL461–EL467.Google Scholar
Collins, F. G. & Zelenevitz, J. 1975 Influence of sound upon separated flow over wings. AIAA J. 13 (3), 408–410.Google Scholar
Desquesnes, G., Terracol, M. & Sagaut, P. 2007 Numerical investigation of the tone noise mechanism over laminar airfoils. J. Fluid Mech. 591, 155–182.Google Scholar
Dovgal, A., Kozlov, V. & Michalke, A. 1994 Laminar boundary layer separation: instability and associated phenomena. Prog. Aerosp. Sci. 30, 61–94.CrossRefGoogle Scholar
Gerakopulos, R. & Yarusevych, S. 2012 Novel time-resolved pressure measurements on an airfoil at a low Reynolds number. AIAA J. 50, 1189–1200.Google Scholar
Golubev, V. V., Nguyen, L., Mankbadi, R. R., Roger, M. & Visbal, M. R. 2014 On flow-acoustic resonant interactions in transitional airfoils. Intl J. Aeroacoust. 13 (11), 1–38.Google Scholar
Hain, R., Kähler, C. J. & Radespiel, R. 2009 Dynamics of laminar separation bubbles at low-Reynolds-number aerofoils. J. Fluid Mech. 630, 129–153.Google Scholar
Howe, M. S. 1998 Acoustics of Fluid–Structure Interactions. Cambridge University Press.Google Scholar
Inasawa, A., Kamijo, T. & Asai, M. 2010 Generation mechanism of trailing-edge noise of airfoil at low Reynolds numbers. In Proceedings of the 13th Asian Congress of Fluid Mechanics, 17–21 December, Dhaka, Bangladesh, pp. 125–128. Bangladesh Society of Mechanical Engineers.Google Scholar
Jones, L. E. & Sandberg, R. D. 2011 Numerical analysis of tonal airfoil self-noise and acoustic feedback-loops. J. Sound Vib. 330, 6137–6152.Google Scholar
Jones, L. E., Sandberg, R. D. & Sandham, N. D. 2008 Direct numerical simulations of forced and unforced separation bubbles on an airfoil at incidence. J. Fluid Mech. 602, 175–207.Google Scholar
Jones, L. E., Sandberg, R. D. & Sandham, N. D. 2010 Stability and receptivity characteristics of a laminar separation bubble on an aerofoil. J. Fluid Mech. 648, 257–296.Google Scholar
Kingan, M. J. & Pearse, J. R. 2009 Laminar boundary layer instability noise produced by an aerofoil. J. Sound Vib. 322, 808–828.CrossRefGoogle Scholar
Lang, M., Rist, U. & Wagner, S. 2004 Investigations on controlled transition development in a laminar separation bubble by means of LDA and PIV. Exp. Fluids 36, 43–52.Google Scholar
Lissaman, P. B. S. 1983 Low-Reynolds-number airfoils. Annu. Rev. Fluid Mech. 15, 223–239.CrossRefGoogle Scholar
Marxen, O. & Henningson, D. S. 2011 The effect of small-amplitude convective disturbances on the size and bursting of a laminar separation bubble. J. Fluid Mech. 671, 1–33.Google Scholar
Marxen, O., Kotapati, R. B., Mittal, R. & Zaki, T. 2015 Stability analysis of separated shear flows subject to control by zero-net-mass-flux jet. Phys. Fluids 27, 024107.Google Scholar
Marxen, O., Lang, M. & Rist, U. 2013 Vortex formation and vortex breakup in a laminar separation bubble. J. Fluid Mech. 728, 58–90.Google Scholar
Marxen, O. & Rist, U. 2010 Mean flow deformation in a laminar separation bubble: separation and stability characteristics. J. Fluid Mech. 660, 37–54.Google Scholar
Mueller, T. J.1985 Low Reynolds number vehicles. Tech. Rep. Report 288. AGARD.Google Scholar
Mueller, T. J. & DeLaurier, J. D. 2003 Aerodynamics of small vehicles. Annu. Rev. Fluid Mech. 35, 98–111.Google Scholar
Nash, E. C., Lowson, M. V. & McAlpine, A. 1999 Boundary layer instability noise on airfoils. J. Fluid Mech. 382, 27–61.Google Scholar
Nishioka, M., Asai, M. & Yoshida, S. 1990 Control of flow separation by acoustic excitation. AIAA J. 28 (11), 1909–1915.Google Scholar
Ol, M. V., McAuliffe, B. R., Hanff, E. S., Scholz, U. & Kähler, C. J.2005 Comparison of laminar separation bubble measurements on a low Reynolds number airfoil in three facilities. In 35th AIAA Fluid Mechanics Conference and Exhibit. AIAA Paper 2005–51049.CrossRefGoogle Scholar
Fosas de Pando, M., Schmid, P. J. & Sipp, D. 2014 A global analysis of tonal noise in flows around aerofoils. J. Fluid Mech. 754, 5–38.Google Scholar
Paterson, R. W., Vogt, P., Fink, M. R. & Munch, C. 1973 Vortex noise of isolated airfoils. J. Aircraft 10 (5), 296–302.Google Scholar
Plogmann, B., Herrig, A. & Würz, W. 2013 Experimental investigations of a trailing edge noise feedback mechanism on a NACA 0012 airfoil. Exp. Fluids 54, 1480, 1–14.Google Scholar
Pröbsting, S., Scarano, F. & Morris, S. C. 2015 Regimes of tonal noise on an airfoil at moderate Reynolds number. J. Fluid Mech. (in press); doi:10.1017/jfm.2015.475.Google Scholar
Pröbsting, S., Serpieri, J. & Scarano, F. 2014 Experimental investigation of aerofoil tonal noise generation. J. Fluid Mech. 747, 656–687.Google Scholar
Raffel, M., Willert, C., Wereley, S. & Kompenhans, J. 2007 Particle Image Velocimetry, 2nd edn. Springer.Google Scholar
Scarano, F. 2003 Theory of non-isotropic spatial resolution in PIV. Exp. Fluids 35, 268–277.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory, 8th edn. Springer.Google Scholar
Schumacher, K. L., Doolan, C. J. & Kelso, R. M. 2014 The effect of a cavity on airfoil tones. J. Sound Vib. 333, 1913–1931.CrossRefGoogle Scholar
Takagi, S. & Konishi, Y. 2010 Frequency selection mechanism of airfoil trailing-edge noise. J. Aircraft 47 (4), 1111–1116.Google Scholar
Tam, C. K. W. 1974 Discrete tones of isolated airfoils. J. Acoust. Soc. Am. 55 (6), 1173–1177.CrossRefGoogle Scholar
Torrence, C. & Compo, G. 1998 A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79 (1), 61–78.Google Scholar
Watmuff, J. H. 1999 Evolution of a wave packet into vortex loops in a laminar separation bubble. J. Fluid Mech. 397, 119–169.Google Scholar
Welch, P. D. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15, 70–73.Google Scholar
Wolf, E., Kähler, C. J., Troolin, D. R., Kykal, C. & Lai, W. 2010 Time-resolved volumetric particle tracking velocimetry of large-scale vortex structures from the reattachment region of a laminar separation bubble to the wake. Exp. Fluids 50, 977–988.Google Scholar
Yarusevych, S., Sullivan, P. E. & Kawall, J. G. 2007 Effect of acoustic excitation amplitude on airfoil boundary layer and wake development. AIAA J. 45 (4), 760–771.Google Scholar
Yarusevych, S., Sullivan, P. E. & Kawall, J. G. 2009 On vortex shedding from an airfoil in low-Reynolds-number flows. J. Fluid Mech. 632, 245–271.Google Scholar
Zaman, K. B. M. Q. & McKinzie, D. J. 1991 Control of laminar separation over airfoils by acoustic excitation. AIAA J. 29 (7), 1075–1083.Google Scholar