Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T20:09:24.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Lagrangian acceleration measurements in convective thermal turbulence

Published online by Cambridge University Press:  06 January 2012

Rui Ni ,
Shi-Di Huang  and
Ke-Qing Xia
Rui Ni
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Shi-Di Huang
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Ke-Qing Xia*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report the first experimental study of Lagrangian acceleration in turbulent Rayleigh–Bénard convection, using particle tracking velocimetry. A method has been developed to quantitatively evaluate and eliminate the uncertainties induced by temperature and refraction index fluctuations caused by the thermal plumes. It is found that the acceleration p.d.f. exhibits a stretched exponential form and that the probability for large magnitude of acceleration in the lateral direction is higher than those in the vertical directions, which can be attributed to the vortical motion of the thermal plumes. The local acceleration variance 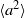was obtained for various values of the three control parameters: the Rayleigh number 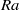(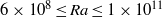), the Prandtl number 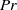( 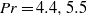and 6.1) and the system size 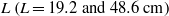. These were then compared with the theoretically predicted dependence on these parameters for buoyancy-dominated turbulent flows and for homogeneous and isotropic turbulence, respectively. It is found that 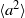in the central region is dominated by contributions from the turbulent background rather than from the buoyancy force, and the Heisenberg–Yaglom relation holds in this region. From this, we obtain the first experimental results of the constant 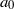of the acceleration variance in the micro-scale Reynolds number range 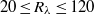, which fills a gap in this constant in the lower 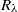end from the experimental side, and provides possible constraints for its high 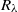behaviour if a certain fitting function is attempted. In addition, acceleration correlation functions were obtained for different 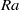. It is found that the zero crossing time of acceleration correlation functions is at 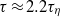( 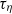is the Kolmogorov time scale) over the range of 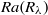spanned in our experiments, which is the same as the simulation results in isotropic turbulence, and the exponential decay time 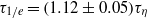, which is larger than 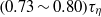found experimentally for other types of turbulent flows with larger .

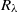JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 692 , 10 February 2012 , pp. 395 - 419
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Adrian, R. J. & Yao, C.-S. 1985 Pulsed laser technique application to liquid and gaseous flows and the scattering power of seed materials. Appl. Opt. 24, 44–52.CrossRefGoogle ScholarPubMed
2.Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
3.Ahlers, G. & Xu, X. 2001 Prandtl-number dependence of heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 86, 3320.CrossRefGoogle ScholarPubMed
4.Calzavarini, E., Lohse, D., Toschi, F. & Tripiccione, R. 2005 Rayleigh and Prandtl number scaling in the bulk Rayleigh–Bénard convection. Phys. Fluids 17, 055107.CrossRefGoogle Scholar
5.Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L. P., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1.CrossRefGoogle Scholar
6.Emran, M.-S. & Schumacher, J. 2010 Lagrangian tracer dynamics in a closed cylindrical turbulent convection cell. Phys. Rev. E 82, 016303.CrossRefGoogle Scholar
7.Falkovich, G., Fouxon, A. & Stepanov, M. G. 2002 Acceleration of rain initiation by cloud turbulence. Nature 419, 151–154.CrossRefGoogle ScholarPubMed
8.Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical samples with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.CrossRefGoogle Scholar
9.Gasteuil, Y., Shew, W. L., Gibert, M., Chillá, F., Castaing, B. & Pinton, J.-F. 2007 Lagrangian temperature, velocity, and local heat flux measurement in Rayleigh–Bénard convection. Phys. Rev. Lett. 99, 234302.CrossRefGoogle ScholarPubMed
10.Gotoh, T. & Fukayama, D. 2001 Pressure spectrum in homogeneous turbulence. Phys. Rev. Lett. 86, 3775.CrossRefGoogle ScholarPubMed
11.Heisenberg, W. 1948 Zur statistichen Theorie der Turbulenz. Z. Phys. 124, 628–657.CrossRefGoogle Scholar
12.Kostinski, A. B. & Shaw, R. A. 2005 Fluctuations and luck in droplet growth by coalescence. Bull. Am. Meteorol. Soc. 86, 235–244.CrossRefGoogle Scholar
13.La Porta, A., Voth, G. A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2001 Fluid particle accelerations in fully developed turbulence. Nature 409, 1017–1019.CrossRefGoogle ScholarPubMed
14.Lohse, D. & Toschi, F. 2003 Ultimate state of thermal convection. Phys. Rev. Lett. 90, 034502.CrossRefGoogle ScholarPubMed
15.Lohse, D. & Xia, K.-Q 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
16.Lüthi, B. 2003 Some aspects of strain, vorticity, and material element dynamics as measured with 3D particle tracking velocimetry in a turbulent flow. PhD thesis, Technische Wissenschaften ETH Zürich.Google Scholar
17.Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics. MIT Press.Google Scholar
18.Mordant, N., Crawford, A. M. & Bodenschatz, E. 2004a Experimental Lagrangian acceleration probability density function measurement. Physica D 193, 245–251.CrossRefGoogle Scholar
19.Mordant, N., Crawford, A. M. & Bodenschatz, E. 2004b Three-dimensional structure of the Lagrangian acceleration in turbulent flows. Phys. Rev. Lett. 93, 214501.CrossRefGoogle ScholarPubMed
20.Mordant, N., Lévêque, E. & Pinton, J.-F. 2004c Experimental and numerical study of the Lagrangian dynamics of high Reynolds turbulence. Phys. Rev. Lett. 6, 116.Google Scholar
21.Mordant, N., Metz, P., Michel, O. & Pinton, J.-F. 2001 Measurement of Lagrangian velocity in fully developed turbulence. Phys. Rev. Lett. 87, 214501.CrossRefGoogle ScholarPubMed
22.Mordant, N., Metz, P., Pinton, J.-F. & Michel, O. 2005 Acoustical technique for Lagrangian velocity measurement. Rev. Sci. Instrum. 76, 025105.CrossRefGoogle Scholar
23.Mordant, N., Delour, J., Léveque, E., Arnéodo, A. & Pinton, J.-F. 2002 Long time correlations in Lagrangian dynamics: a key to intermittency in turbulence. Phys. Rev. Lett. 89, 254502.CrossRefGoogle ScholarPubMed
24.Ni, R., Huang, S.-D. & Xia, K.-Q. 2011 Local energy dissipation rate balances local heat flux in the centre of turbulent thermal convection. Phys. Rev. Lett. 107, 174503.CrossRefGoogle ScholarPubMed
25.Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.CrossRefGoogle ScholarPubMed
26.Qiu, X.-L., Shang, X.-D., Tong, P. & Xia, K.-Q. 2004 Velocity oscillations in turbulent Rayleigh–Bénard convection. Phys. Fluids 16, 412–423.CrossRefGoogle Scholar
27.Qureshi, N. M., Bourgoin, M., Bauder, C., Cartellier, A. & Gagne, Y. 2007 Turbulent transport of material particles: an experimental study of finite size effects. Phys. Rev. Lett. 99, 184502.CrossRefGoogle ScholarPubMed
28.Reade, W. C. 1998 Direct numerical simulation of turbulent aerosol coagulation. PhD thesis, The Pennsylvania State University.Google Scholar
29.Sawford, B. 2001 Turbulent relative dispersion. Annu. Rev. Fluid Mech. 33, 289–317.CrossRefGoogle Scholar
30.Sawford, B. L., Yeung, P. K., Borgas, M. S., Vedula, P., La Porta, A., Crawford, A. M. & Bodenschatz, E. 2003 Conditional and unconditional acceleration statistics in turbulence. Phy. Fluids 15, 3478.CrossRefGoogle Scholar
31.Schumacher, J. 2008 Lagrangian dispersion and heat transport in convective turbulence. Phys. Rev. Lett. 100, 134502.CrossRefGoogle ScholarPubMed
32.Shang, X.-D., Qiu, X.-L., Tong, P. & Xia, K.-Q. 2003 Measured local heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 90, 074501.CrossRefGoogle ScholarPubMed
33.Shang, X.-D, Tong, P. & Xia, K.-Q. 2008 Scaling of the local convective heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 100, 244503.CrossRefGoogle ScholarPubMed
34.Shew, W. L., Gasteuil, Y., Gibert, M., Metz, P. & Pinton, J.-F. 2007 Instrumented tracer for Lagrangian measurements in Rayleigh–Bénard convection. Rev. Sci. Instrum. 78, 065105.CrossRefGoogle ScholarPubMed
35.Shraiman, B.-I. & Siggia, E.-D. 1990 Heat transport in high-Rayleigh number convection. Phys. Rev. A 42, 3650–3653.CrossRefGoogle ScholarPubMed
36.Shraiman, B.-I. & Siggia, E.-D. 2000 Scalar turbulence. Nature 405, 639–646.CrossRefGoogle ScholarPubMed
37.Siggia, E.-D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.CrossRefGoogle Scholar
38.Sun, C., Xia, K.-Q. & Tong, P. 2005 Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72 (2), 026302.CrossRefGoogle Scholar
39.Sun, C., Zhou, Q. & Xia, K.-Q. 2006 Cascades of velocity and temperature fluctuations in buoyancy-driven thermal turbulence. Phys. Rev. Lett. 97 (14), 144504.CrossRefGoogle ScholarPubMed
40.Taylor, G. I. 1921 Diffusion by continuous movements. Proc. Lond. Math. Soc. 20, 196–211.Google Scholar
41.Vedula, P. & Yeung, P. K. 1999 Similarity scaling of acceleration and pressure statistics in numerical simulations of isotropic turbulence. Phys. Fluids 11, 1208.CrossRefGoogle Scholar
42.Virant, M. & Dracos, T. 1997 3D PTV and its application on Lagrangian motion. Meas. Sci. Technol. 8, 1539–1552.CrossRefGoogle Scholar
43.Volk, R., Mordant, N., Verhille, G. & Pinton, J.-F. 2008 Laser Doppler measurement of inertial particle and bubble accelerations in turbulence. Europhys. Lett. 81, 34002.CrossRefGoogle Scholar
44.Voth, G. A., La Porta, A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.CrossRefGoogle Scholar
45.Voth, G. A., La Porta, A., Crawford, A. M., Bodenschatz, E., Ward, C. & Alexander, J. 2001 A silicon strip detector system for high resolution particle tracking in turbulence. Rev. Sci. Instrum. 72, 4348–4353.CrossRefGoogle Scholar
46.Willneff, J. 2003 A spatio-temporal matching algorithm for 3D particle tracking velocimetry. PhD thesis, Technische Wissenschaften ETH Zürich.Google Scholar
47.Xi, H.-D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.CrossRefGoogle Scholar
48.Xi, H.-D. & Xia, K.-Q. 2008 Azimuthal motion, reorientation, cessation and reversal of the large-scale circulation in turbulent thermal convection: a comparison between aspect ratio one and one-half geometries. Phys. Rev. E 78, 036326.CrossRefGoogle Scholar
49.Xia, K.-Q. 2011 How heat transfer efficiencies in turbulent thermal convection depend on internal flow modes. J. Fluid Mech. 676, 1–4.CrossRefGoogle Scholar
50.Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.CrossRefGoogle ScholarPubMed
51.Xia, K.-Q. & Lui, S.-L. 1997 Turbulent thermal convection with an obstructed sidewall. Phys. Rev. Lett. 79, 5006.CrossRefGoogle Scholar
52.Yaglom, A. M. 1949 On the acceleration field in a turbulent flow. C. R. Akad. URSS 67 (5), 795–798.Google Scholar
53.Yeung, P.-K. 2002 Lagrangian investigations of turbulence. Annu. Rev. Fluid Mech. 34, 115142.CrossRefGoogle Scholar
54.Yeung, P. K. & Pope, S. B. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207, 531–586.CrossRefGoogle Scholar
55.Zhou, Q., Sun, C. & Xia, K.-Q. 2007 Morphological evolution of thermal plumes in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 074501.CrossRefGoogle ScholarPubMed
56.Zhou, Q., Sun, C. & Xia, K.-Q 2008 Experimental investigation of homogeneity, isotropy, and circulation of the velocity field in buoyancy-driven turbulence. J. Fluid Mech. 598, 361–372.CrossRefGoogle Scholar
57.Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.CrossRefGoogle Scholar