Published online by Cambridge University Press: 11 December 2017
A comprehensive experimental study is presented to analyse the instabilities of a magnetic fluid drop surrounded by miscible fluid confined in a Hele-Shaw cell. The experimental conditions include different magnetic fields (by varying the maximum pre-set magnetic field strengths, 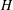 $H$, and sweep rates,
$H$, and sweep rates, 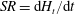 $SR=\text{d}H_{t}/\text{d}t$, where
$SR=\text{d}H_{t}/\text{d}t$, where 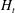 $H_{t}$ is the instant magnetic field strength), gap spans,
$H_{t}$ is the instant magnetic field strength), gap spans, 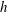 $h$, and magnetic fluid samples, and are further coupled into a modified Péclect number
$h$, and magnetic fluid samples, and are further coupled into a modified Péclect number 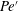 $Pe^{\prime }$ to evaluate the instabilities. Two distinct instabilities are induced by the external magnetic fields with different sweep rates: (i) a labyrinthine fingering instability, where small fingerings emerge around the initial circular interface in the early period, and (ii) secondary waves in the later period. Based on 81 sets of experimental conditions, the initial growth rate of the interfacial length,
$Pe^{\prime }$ to evaluate the instabilities. Two distinct instabilities are induced by the external magnetic fields with different sweep rates: (i) a labyrinthine fingering instability, where small fingerings emerge around the initial circular interface in the early period, and (ii) secondary waves in the later period. Based on 81 sets of experimental conditions, the initial growth rate of the interfacial length,  $\unicode[STIX]{x1D6FC}$, of the magnetic drop is found to increase linearly with
$\unicode[STIX]{x1D6FC}$, of the magnetic drop is found to increase linearly with 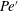 $Pe^{\prime }$, indicating that
$Pe^{\prime }$, indicating that  $\unicode[STIX]{x1D6FC}$ is proportional to the square root of the
$\unicode[STIX]{x1D6FC}$ is proportional to the square root of the 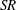 $SR$ and
$SR$ and 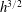 $h^{3/2}$ at the onset of the labyrinthine instability. In addition, secondary waves, which are characterised by the dimensionless wavelength
$h^{3/2}$ at the onset of the labyrinthine instability. In addition, secondary waves, which are characterised by the dimensionless wavelength 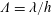 $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D706}/h$, can only be triggered when the three-dimensional magnetic microconvection is strong enough to make
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D706}/h$, can only be triggered when the three-dimensional magnetic microconvection is strong enough to make 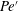 $Pe^{\prime }$ exceed a critical value, i.e.
$Pe^{\prime }$ exceed a critical value, i.e. 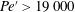 $Pe^{\prime }>19\,000$, where
$Pe^{\prime }>19\,000$, where 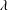 $\unicode[STIX]{x1D706}$ is the wavelength of the secondary wave. In this flow regime of high
$\unicode[STIX]{x1D706}$ is the wavelength of the secondary wave. In this flow regime of high 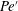 $Pe^{\prime }$, the length scale of the secondary wave instability is found to be
$Pe^{\prime }$, the length scale of the secondary wave instability is found to be 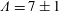 $\unicode[STIX]{x1D6EC}=7\pm 1$, corresponding to the Stokes regime; meanwhile, in the flow regime of low
$\unicode[STIX]{x1D6EC}=7\pm 1$, corresponding to the Stokes regime; meanwhile, in the flow regime of low 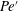 $Pe^{\prime }$, the flow corresponds to the Hele-Shaw regime introduced by Fernandez et al. (J. Fluid Mech., vol. 451, 2002, pp. 239–260).
$Pe^{\prime }$, the flow corresponds to the Hele-Shaw regime introduced by Fernandez et al. (J. Fluid Mech., vol. 451, 2002, pp. 239–260).
The first and second authors contributed equally to this work.