Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-09T06:52:23.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Kinetics and prey capture by a paddling jellyfish: three-dimensional simulation and Lagrangian coherent structure analysis

Published online by Cambridge University Press:  15 February 2021

Mazyar Dawoodian  and
Amalendu Sau Open the ORCID record for Amalendu Sau [Opens in a new window]
Mazyar Dawoodian
Affiliation:
Department of Aerospace and Software Engineering, Gyeongsang National University, Jinju660701, South Korea
Amalendu Sau*
Affiliation:
Department of Aerospace and Software Engineering, Gyeongsang National University, Jinju660701, South Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

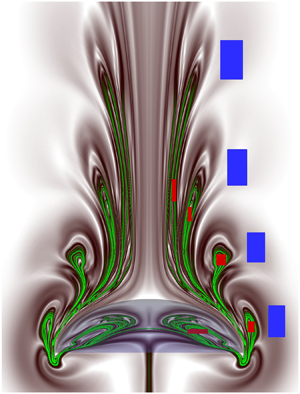
Three-dimensional simulations are performed to investigate swimming and prey capture by a paddling jellyfish. First, the three-dimensional vortex–vortex and vortex–body interactions are revealed, as the jellyfish swims forwards through several cycles of active muscle contraction followed by passive energy recapture via shape recovery. For varied transient paddling force and paddling frequency, we analyse the resultant changes of a jellyfish's swimming speed, interactive power, cost of transport and prey clearance rate. The pressure field around the periodically deformed elastic bell and the circulation generated by starting and stopping vortex rings are presented in greater detail to better understand the biophysical interactions that support swimming. Second, to reveal prey-specific interception and feeding behaviour, using a dynamical-system-based approach and modified Maxey–Riley equation, we compute the trajectories of the surrounding infinitesimal, inertial, opposite and normally escaping prey or plankton that hover around the medusa and are swept differently via the paddling-created velocity field. Accordingly, the diverse prey trajectories are obtained with varied paddling force, resonant driving of the elastic bell and for two different bell fineness ratios. These trajectories are then used to compute the finite-time Lyapunov exponent fields and identify particle Lagrangian coherent structures for various motile/strategically evasive prey, for five swimming cycles. The detected geometric separatrices unambiguously map and demarcate differently driven upstream fluid regions of a medusa and illustrate precisely from where an intercepted prey can be brought into the jellyfish bell, or safely stored in a capture region for ingestion, and from where a prey will surely escape. Hereby, for the first time, the prey-specific target regions, the physically well-defined three-dimensional capture surfaces and the generated cycle-to-cycle prey clearance rate are presented/analysed like never before, which provide a significantly advanced understanding on diverse predator–prey interactions and resultant success rate in prey capture. Several supplementary movies that show detailed fluid–structure interactions, transient entrainment of the floating prey and eventual prey confinement inside a secured capture surface are provided for two different jellyfish morphologies (fineness ratios 0.3 and 0.5) that help to better comprehend the natural prey encounter and hunting processes.

JFM classification

Biological Fluid Dynamics: Swimming/flying Biological Fluid Dynamics: Propulsion
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 912 , 10 April 2021 , A41
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acuna, J.L., Lopez-Urrutia, A. & Colin, S. 2011 Faking giants: the evolution of high prey clearance rates in jellyfishes. Science 333, 1627–1629.CrossRefGoogle ScholarPubMed
Alben, S., Miller, L.A. & Peng, J. 2013 Efficient kinematics for jet-propelled swimming. J. Fluid Mech. 733, 100–133.CrossRefGoogle Scholar
Alexander, R.M.C.N. & Bennet-Clark, H.C. 1977 Storage of elastic strain energy in muscle and other tissues. Nature 265 (5590), 114–117.CrossRefGoogle ScholarPubMed
Ali, S. & Shah, M. 2007 A Lagrangian particle dynamics approach for crowd flow segmentation and stability analysis. In IEEE Conference on Computer Vision and Pattern Recognition, p. 4270002.Google Scholar
Babiano, A., Cartwright, J.H.E., Piro, O. & Provenzale, A. 2000 Dynamics of a small neutrally buoyant sphere in a fluid and targeting in Hamiltonian systems. Phys. Rev. Lett. 84, 5764–5767.CrossRefGoogle Scholar
Colin, S.P. & Costello, J.H. 2002 Morphology, swimming performance, and propulsive mode of six co-occurring hydromedusae. J. Exp. Biol. 205, 427–437.Google ScholarPubMed
Colin, S.P., Costello, J.H., Dabiri, J.O., Villanueva, A., Blottman, J.B., Gemmell, B.J. & Priya, S. 2012 Biomimetic and live medusae reveal the mechanistic advantages of a flexible bell margin. PloS One 7 (11), e48909.CrossRefGoogle ScholarPubMed
Colin, S.P., Costello, J.H. & Kordula, H. 2006 Upstream foraging by medusae. Mar. Ecol. Prog. Ser. 327, 143–155.CrossRefGoogle Scholar
Costello, J.H. & Colin, S.P. 1995 Flow and feeding by swimming scyphomedusae. Mar. Biol. 124, 399–406.CrossRefGoogle Scholar
Dabiri, J.O., Colin, S.P., Costello, J.H. & Gharib, M. 2005 Vortex motion in the ocean: in situ visualization of jellyfish swimming and feeding flows. Phys. Fluids 17, 091108.CrossRefGoogle Scholar
Darwin, C. 1953 Note on hydrodynamics. Proc. Camb. Phil. Soc. 49, 342–354.CrossRefGoogle Scholar
Demont, M.E. & Gosline, J.M. 1988 Mechanics of jet propulsion in the hydromedusan jellyfish, Polyorchis penicillatus: I, mechanical properties of the locomotor structure. J. Expl Biol. 134, 313–332.Google Scholar
D’humieres, D., Ginzburg, I., Krefczyk, M., Lallemand, P. & Luo, L.S. 2002 Multiple relaxation time lattice Boltzmann models in three dimensions. Proc. R. Soc. Lond. A 360, 367.Google ScholarPubMed
Fields, D.M. & Yen, J. 1997 The escape behavior of marine copepods in response to a quantifiable fluid mechanical disturbance. J. Plankton Res. 19, 1289–1304.CrossRefGoogle Scholar
Floryan, D., Buren, T.V. & Smits, A.J. 2018 Efficient cruising for swimming and flying animals is dictated by fluid drag. Proc. Natl Acad. Sci. USA 115, 8116–8118.CrossRefGoogle ScholarPubMed
Ford, M.D., Costello, J.H. & Klos, E. 1997 Swimming and feeding by the scyphomedusa Chrysaora quinquecirrha. Mar. Biol. 129, 355–362.CrossRefGoogle Scholar
Franco, E., Pekarek, D.N., Peng, J. & Dabiri, J.O. 2007 Geometry of unsteady fluid transport during fluid–structure interactions. J. Fluid Mech. 589, 125–145.CrossRefGoogle Scholar
Gemmell, B.J., Colin, S.P., Costello, J.H. & Dabiri, J.O. 2015 Suction-based propulsion as a basis for efficient animal swimming. Nature Commun. 6, 8790.CrossRefGoogle ScholarPubMed
Gemmell, B.J., Costello, J.H., Colin, S.P., Stewart, C.J., Dabiri, J.O., Tafti, D. & Priya, S. 2013 Passive energy recapture in jellyfish contributes to propulsive advantage over other metazoans. Proc. Natl Acad. Sci. USA 110, 17904.CrossRefGoogle ScholarPubMed
Green, M.A., Rowley, C.W. & Haller, G. 2007 Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 572, 111–120.CrossRefGoogle Scholar
Haller, G. 2001 Lagrangian structures and the rate of strain in a partition of two-dimensional turbulence. Phys. Fluids 13, 3365–3385.CrossRefGoogle Scholar
Haller, G. 2015 Lagrangian coherent structures. Annu. Rev. Fluid Mech. 47, 137–161.CrossRefGoogle Scholar
Hamlet, C., Strychalski, W. & Miller, L. 2020 Fluid dynamics of ballistic strategies in nematocyst firing. Fluids 5, 20.CrossRefGoogle Scholar
Hansson, L.J. & Kiørboe, T. 2006 Prey-specific encounter rates and handling efficiencies as causes of prey selectivity in ambush-feeding hydromedusae. Limnol. Oceanogr. 51, 1849–1858.CrossRefGoogle Scholar
Hoover, A.P., Griffith, B.E. & Miller, L.A. 2017 Quantifying performance in the medusa mechanospace with an actively swimming three-dimensional jellyfish model. J. Fluid Mech. 813, 1112–1155.CrossRefGoogle Scholar
Hoover, A.P., Porras, A. & Miller, L.A. 2019 Pump or coast: the role of resonance and passive energy recapture in medusa swimming performance. J. Fluid Mech. 863, 1031–1061.CrossRefGoogle Scholar
Huang, W.X. & Sung, H.J. 2009 An immersed boundary method for fluid–flexible structure interaction. Comput. Meth. Appl. Mech. Engng 198, 2650–2661.CrossRefGoogle Scholar
Humphries, S. 2009 Filter feeders and plankton increase particle encounter rates through flow regime control. Proc. Natl Acad. Sci. USA 106, 1782–1787.CrossRefGoogle ScholarPubMed
Katija, K., Beaulieu, W.T., Regula, C., Colin, S.P., Costello, J.H. & Dabiri, J.O. 2011 Quantification of flows generated by the hydromedusa Aequorea victoria: a Lagrangian coherent structure analysis. Mar. Ecol. Prog. Ser. 435, 111–123.CrossRefGoogle Scholar
Katija, K. & Dabiri, J.O. 2009 A viscosity-enhanced mechanism for biogenic ocean mixing. Nature 460, 624–626.CrossRefGoogle ScholarPubMed
Kiørboe, T. 2011 How zooplankton feed: mechanisms, traits and trade-offs. Biol. Rev. 86, 311–339.CrossRefGoogle ScholarPubMed
Kiørboe, T., Andersen, A., Langlois, V.J. & Jakobsen, H.H. 2010 Unsteady motion: escape jumps in planktonic copepods, their kinematics and energetics. J. R. Soc. Interface 7, 1591–1602.CrossRefGoogle ScholarPubMed
Kiørboe, T., Jiang, H., Goncalves, R.J., Hielsen, L.T. & Wadhwa, N. 2014 Flow disturbances generated by feeding and swimming zooplankton. Proc. Natl Acad. Sci. USA 111, 11738–11743.CrossRefGoogle ScholarPubMed
Kiørboe, T., Saiz, E. & Visser, A. 1999 Hydrodynamic signal perception in the copepod Acartia tonsa. Mar. Ecol. Prog. Ser. 179, 97–111.CrossRefGoogle Scholar
Kruger, T., Kusumaatmaja, H., Kuzmin, A., Shardt, O., Silva, G. & Viggen, E.M. 2016 The Lattice Boltzmann Method – Principles and Practice. Springer.Google Scholar
Kruger, T., Varnik, F. & Raabe, D. 2011 Efficient and accurate simulations of deformable particles immersed in a fluid using a combined immersed boundary lattice Boltzmann finite element method. Comput. Maths Applics. 61, 3485–3505.CrossRefGoogle Scholar
Kuzmin, A., Guo, Z.L. & Mohamad, A.A. 2011 Simultaneous incorporation of mass and force terms in the multi-relaxation-time framework of the lattice Boltzmann schemes. Phil. Trans. R. Soc. 369, 2219–2227.CrossRefGoogle ScholarPubMed
Maxey, M.R. & Riley, J.J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.CrossRefGoogle Scholar
Mchenry, M.J. & Jed, J. 2003 The ontogenetic scaling of hydrodynamics and swimming performance in jellyfish (Aurelia aurita). J. Expl Biol. 206 (22), 4125–4137.CrossRefGoogle Scholar
Megill, W.M., Gosline, J.M. & Blake, R.W. 2005 The modulus of elasticity of fibrillin-containing elastic fibres in the mesoglea of the hydromedusa Polyorchis penicillatus. J. Expl Biol. 208, 3819–3834.CrossRefGoogle ScholarPubMed
Michaelides, E.E. 1997 Review – the transient equation of motion for particles, bubbles, and droplets. J. Trans. ASME Fluids Engng 119, 233–247.CrossRefGoogle Scholar
Miles, J.G. & Battista, N. 2019 Naut your everyday jellyfish model: exploring how tentacles and oral arms impact locomotion. Fluids 4, 169.CrossRefGoogle Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261.CrossRefGoogle Scholar
Nielsen, T.L., Asadzadeh, S.S., Dolger, J., Walther, J.H., Kiørboe, T. & Andersen, A. 2017 Hydrodynamics of microbial filter feeding. Proc. Natl Acad. Sci. USA 114, 9373–9378.CrossRefGoogle ScholarPubMed
Park, S.G., Chang, C.B., Huang, W.X. & Sung, H.J. 2014 Simulation of swimming oblate jellyfish with a paddling based locomotion. J. Fluid Mech. 748, 731–755.CrossRefGoogle Scholar
Peng, J. & Alben, S. 2012 Effects of shape and stroke parameters on the propulsion performance of an axisymmetric swimmer. Bioinspir. Biomim. 7, 016012.CrossRefGoogle ScholarPubMed
Peng, J. & Dabiri, J.O. 2009 Transport of inertial particles by Lagrangian coherent structures: application to predator–prey interaction in jellyfish feeding. J. Fluid Mech. 623, 75–84.CrossRefGoogle Scholar
Premnath, K.N. & Abraham, J. 2007 Three-dimensional multi-relaxation time (MRT) lattice-Boltzmann models for multiphase flow. J. Comput. Phys. 224, 539–569.CrossRefGoogle Scholar
Sahin, M., Mohseni, K. & Colin, S.P. 2009 The numerical comparison of flow patterns and propulsive performances for the hydromedusae Sarsia tubulosa and Aequorea victoria. J. Expl Biol. 212, 2656–2667.CrossRefGoogle ScholarPubMed
Shadden, S.C., Dabiri, J.O. & Marsden, J.E. 2006 Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 18, 047105.CrossRefGoogle Scholar
Shin, S.J., Huang, W.-X. & Sung, H.J. 2008 Assessment of regularized delta functions and feedback forcing schemes for an immersed boundary method. Intl J. Numer. Meth. Fluids 58, 263–286.CrossRefGoogle Scholar
Strickler, J.R. 1975 Swimming of planktonic Cyclops species (Copepoda, Crustacea): pattern, movements and their control. In Swimming and Flying in Nature (ed. T.Y.T. Wu, C.J. Brokaw & C. Brennan), pp. 599–613. Plenum.CrossRefGoogle Scholar
Taylor, G.K., Nudds, R.L. & Thomas, A.L.R. 2003 Flying and swimming animals cruise at a strouhal number tuned for high power efficiency. Nature 425, 707–711.CrossRefGoogle Scholar
Tsubota, K., Wada, S. & Yamaguchi, T. 2006 Simulation study on effects of hematocrit on blood flow properties using particle method. J. Biomech. Sci. Engng 1, 159–170.CrossRefGoogle Scholar
Tytell, E.D., Hsu, C.-Y., Williams, T.L., Cohen, A.H. & Fauci, L.J. 2010 Interactions between internal forces, body stiffness, and fluid environment in a neuromechanical model of lamprey swimming. Proc. Natl Acad. Sci. USA 107 (46), 19832–19837.CrossRefGoogle Scholar
Viitasalo, M., Kiørboe, T., Flinkman, J., Pedersen, L.W. & Visser, A.W. 1998 Predation vulnerability of planktonic copepods: consequences of predator foraging strategies and prey sensory abilities. Mar. Ecol. Prog. Ser. 175, 129–142.CrossRefGoogle Scholar
Wilson, M.M., Peng, J., Dabiri, J. & Eldredge, J.D. 2009 Lagrangian coherent structures in low Reynolds number swimming. J. Phys.: Condens. Matter 21, 204105.Google ScholarPubMed
Wu, J., Cheng, Y., Zhang, C. & Wei, D. 2015 Three-dimensional simulation of balloon dynamics by the immersed boundary method coupled to the multiple-relaxation-time lattice Boltzmann method. Commun. Comput. Phys. 17, 1271–1300.CrossRefGoogle Scholar
Yang, X., Zhang, X., Li, Z. & He, G.W. 2009 A smoothing technique for discrete delta functions with application to immersed boundary method in moving boundary simulations. J. Comput. Phys. 228, 7821–7836.CrossRefGoogle Scholar
Zhao, H., Freund, J.B. & Moser, R.D. 2008 A fixed-mesh method for incompressible flow–structure systems with finite solid deformations. J. Comput. Phys. 227, 3114–3140.CrossRefGoogle Scholar
Zhu, L., He, G., Wang, S., Miller, L., Zhang, X., You, Q. & Fang, S. 2011 An immersed boundary method based on the lattice Boltzmann approach in three-dimension, with application. Comput. Maths Applics. 61, 3506–3518.CrossRefGoogle Scholar
Supplementary material: File

Dawoodian and Sau supplementary movie 1

See word file for movie caption

Download Dawoodian and Sau supplementary movie 1(File)
File 7.9 MB
Supplementary material: File

Dawoodian and Sau supplementary movie 2

See word file for movie caption

Download Dawoodian and Sau supplementary movie 2(File)
File 4.4 MB
Supplementary material: File

Dawoodian and Sau supplementary movie 3

See word file fro movie caption

Download Dawoodian and Sau supplementary movie 3(File)
File 14.1 MB
Supplementary material: File

Dawoodian and Sau supplementary movie 4

See word file for movie caption

Download Dawoodian and Sau supplementary movie 4(File)
File 10.9 MB
Supplementary material: File

Dawoodian and Sau supplementary movie 5

See word file for movie caption

Download Dawoodian and Sau supplementary movie 5(File)
File 5.3 MB
Supplementary material: File

Dawoodian and Sau supplementary movie 6

See word file for movie caption

Download Dawoodian and Sau supplementary movie 6(File)
File 10.6 MB
Supplementary material: File

Dawoodian and Sau supplementary movie 7

See word file for movie caption

Download Dawoodian and Sau supplementary movie 7(File)
File 13.2 MB
Supplementary material: File

Dawoodian and Sau supplementary material

Captions for movies 1-7

Download Dawoodian and Sau supplementary material(File)
File 116.4 KB