Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T11:31:09.277Z Has data issue: false hasContentIssue false
  • English
  • Français

Intrinsic features of flow past three square prisms in side-by-side arrangement

Published online by Cambridge University Press:  15 August 2017

Qinmin Zheng  and
Md. Mahbub Alam Open the ORCID record for Md. Mahbub Alam [Opens in a new window]
Qinmin Zheng
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China
Md. Mahbub Alam*
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China Shenzhen Digital Engineering Laboratory of Offshore Equipment, Shenzhen, China
*
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An investigation on the flow around three side-by-side square prisms can provide a better understanding of complicated flow physics associated with multiple, closely spaced structures in which more than one gap flow is involved. In this paper, the flow around three side-by-side square prisms at a Reynolds number 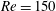$Re=150$ is studied systematically at 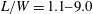$L/W=1.1{-}9.0$, where 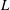$L$ is the prism centre-to-centre spacing and 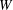$W$ is the prism width. Five distinct flow structures and their ranges are identified, viz. base-bleed flow (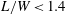$L/W<1.4$), flip-flopping flow 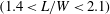$(1.4<L/W<2.1)$, symmetrically biased beat flow 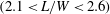$(2.1<L/W<2.6)$, non-biased beat flow 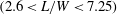$(2.6<L/W<7.25)$ and weak interaction flow 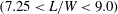$(7.25<L/W<9.0)$. Physical aspects of each flow regime, such as vortex structures, vortex dynamics, gap-flow behaviours, shedding frequencies and fluid forces, are discussed in detail. A secondary (beat) frequency other than the Strouhal frequency (primary frequency) is observed in the symmetrically biased and non-biased beat flows, associated with the beat-like modulation in 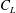$C_{L}$-peak or amplitude, where 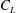$C_{L}$ is the lift force coefficient. Here we reveal the generic and intrinsic origin of the secondary frequency, establishing its connections with the phase lag between the two shear-layer sheddings from the two sides of a gap. When the two sheddings are in phase, no viscous force acts at the interface (i.e. at the centreline of the gap) of the two sheddings, resulting in the largest fluctuations in streamwise momentum, streamwise velocity and pressure; the maximum 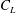$C_{L}$ amplitude thus features the in-phase shedding. Conversely, when the two sheddings are antiphase, a viscous force exists at the interface of the two sheddings and restricts the momentum fluctuation through the gap, yielding a minimum 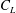$C_{L}$ amplitude. When the phase relationship between the two sheddings changes from in phase to antiphase, the extra viscous force acting at the interface becomes larger and causes the 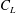$C_{L}$ amplitude to change from a maximum to a minimum.

JFM classification

Vortex Flows: Vortex dynamics Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 996 - 1033
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achenbach, E. 1968 Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to Re = 5 × 106 . J. Fluid Mech. 34, 625–639.CrossRefGoogle Scholar
Agrawal, A., Djenidi, L. & Antonia, R. A. 2006 Investigation of flow around a pair of side-by-side square cylinders using the lattice Boltzmann method. Comput. Fluids 35, 1093–1107.CrossRefGoogle Scholar
Alam, M. M., Bai, H. L. & Zhou, Y. 2016 The wake of two staggered square cylinders. J. Fluid Mech. 801, 475–507.Google Scholar
Alam, M. M., Moriya, M. & Sakamoto, H. 2003 Aerodynamic characteristics of two side-by-side circular cylinders and application of wavelet analysis on the switching phenomenon. J. Fluids Struct. 18, 325–346.CrossRefGoogle Scholar
Alam, M. M. & Zhou, Y. 2007 Flow around two side-by-side closely spaced circular cylinders. J. Fluids Struct. 23, 799–805.Google Scholar
Alam, M. M. & Zhou, Y. 2013 Intrinsic features of flow around two side-by-side square cylinders. Phys. Fluids 25, 085106.Google Scholar
Alam, M. M., Zhou, Y. & Wang, X. W. 2011 The wake of two side-by-side square cylinders. J. Fluid Mech. 669, 432–471.Google Scholar
Bearman, P. W. 1967 On vortex street wakes. J. Fluid Mech. 28, 625–641.Google Scholar
Chatterjee, D., Biswas, G. & Amiroudine, S. 2010 Numerical simulation of flow past row of square cylinders for various separation ratios. Comput. Fluids 39, 49–59.Google Scholar
Griffin, O. M. 1978 A universal Strouhal number for the ‘locking-on’ of vortex shedding to the vibrations of bluff cylinders. J. Fluid Mech. 85, 591–606.CrossRefGoogle Scholar
Inoue, O. & Suzuki, Y. 2007 Beat of sound generated by flow past three side-by-side square cylinders. Phys. Fluids 19, 48102.Google Scholar
Issa, R. I. 1986 Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.Google Scholar
Kolar, V., Lyn, D. A. & Rodi, W. 1997 Ensemble-averaged measurements in the turbulent near wake of two side-by-side square cylinders. J. Fluid Mech. 346, 201–237.CrossRefGoogle Scholar
Kumada, M., Hiwada, M., Ito, M. & Mabuchi, I. 1984 Wake interference between three circular cylinders arranged side by side normal to a flow. Trans. JSME 50, 1699–1707.Google Scholar
Kumar, S. R., Sharma, A. & Agrawal, A. 2008 Simulation of flow around a row of square cylinders. J. Fluid Mech. 606, 369–397.Google Scholar
Lee, B. E. 1975 The effect of turbulence on the surface pressure field of a square prism. J. Fluid Mech. 69, 263–282.CrossRefGoogle Scholar
Le Gal, P., Peschard, I., Chauve, M. P. & Takeda, Y. 1996 Collective behavior of wakes downstream a row of cylinders. Phys. Fluids 8, 2097–2106.Google Scholar
Mizushima, J. & Hatsuda, G. 2014 Nonlinear interactions between the two wakes behind a pair of square cylinders. J. Fluid Mech. 759, 295–320.Google Scholar
Okajima, A. 1982 Strouhal numbers of rectangular cylinders. J. Fluid Mech. 123, 379–398.Google Scholar
Park, D. & Yang, K. 2016 Flow instabilities in the wake of a rounded square cylinder. J. Fluid Mech. 793, 915–932.Google Scholar
Prasanth, T. K. & Mittal, S. 2008 Vortex-induced vibrations of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 594, 463–491.Google Scholar
Richter, A. & Naudascher, E. 1976 Fluctuating forces on a rigid circular cylinder in confined flow. J. Fluid Mech. 78, 561–576.CrossRefGoogle Scholar
Roshko, A.1954. On the drag and shedding frequency of two-dimensional bluff bodies. NACA Tech. Notes.Google Scholar
Saha, A. K., Biswas, G. & Muralidhar, K. 2003 Three-dimensional study of flow past a square cylinder at low Reynolds numbers. Intl J. Heat Fluid Flow 24, 54–66.CrossRefGoogle Scholar
Sewatkar, C. M., Patel, R., Sharma, A. & Agrawal, A. 2012 Flow around six in-line square cylinders. J. Fluid Mech. 710, 195–233.CrossRefGoogle Scholar
Sewatkar, C. M., Sharma, A. & Agrawal, A. 2009 On the effect of Reynolds number for flow around a row of square cylinders. Phys. Fluids 21, 083602.Google Scholar
Sewatkar, C. M., Sharma, A. & Agrawal, A. 2011 Simulation of flow across a row of transversely oscillating square cylinders. J. Fluid Mech. 680, 361–397.CrossRefGoogle Scholar
Sharma, A. & Eswaran, V. 2004 Heat and fluid flow across a square cylinder in the two-dimensional laminar flow regime. Numer. Heat Transfer A 45, 247–269.Google Scholar
Sohankar, A. 2006 Flow over a bluff body from moderate to high Reynolds numbers using large eddy simulation. Comput. Fluids 35, 1154–1168.Google Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1999 Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 11, 288–306.Google Scholar
Sumner, D., Price, S. J. & Paidoussis, M. P. 2000 Flow-pattern identification for two staggered circular cylinders in cross-flow. J. Fluid Mech. 411, 263–303.Google Scholar
Tong, F., Cheng, L., Zhao, M. & An, H. 2015 Oscillatory flow regimes around four cylinders in a square arrangement under small KC and Re conditions. J. Fluid Mech. 769, 298–336.Google Scholar
Versteeg, H. K. & Malalasekera, W. 2007 An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Pearson Education.Google Scholar
West, G. S. & Apelt, C. J. 1982 The effects of tunnel blockage and aspect ratio on the mean flow past a circular cylinder with Reynolds numbers between 104 and 105 . J. Fluid Mech. 114, 361–377.Google Scholar
Yoon, D., Yang, K. & Choi, C. 2010 Flow past a square cylinder with an angle of incidence. Phys. Fluids 22, 43603.Google Scholar
Zdravkovich, M. M. 1997 Flow around Circular Cylinders, vol. 1: Fundamentals. Oxford University Press.Google Scholar