The stability of open-channel flows (or film flows) has been extensively investigated for the case of impermeable smooth walls. In contrast, despite its relevance in many geophysical and industrial flows, the case that considers a permeable rather than an impermeable wall is almost unexplored. In the present work, a linear stability analysis of a film falling over a permeable and inclined wall is developed and discussed. The focus is on the mutual interaction between three modes of instability, namely, the well-known free-surface and hydrodynamic (i.e. shear) modes, which are commonly observed in open-channel flows over impermeable walls, plus a new one associated with the flow within the permeable wall (i.e. the porous mode). The flow in this porous region is modelled by the volume-averaged Navier–Stokes equations and, at the wall interface, the surface and subsurface flow are coupled through a stress-jump condition, which allows one to obtain a continuous velocity profile throughout the whole flow domain. The generalized eigenvalue problem is then solved via a novel spectral Galerkin method, and the whole spectrum of eigenvalues is presented and physically interpreted. The results show that, in order to perform an analysis with a full coupling between surface and subsurface flow, the convective terms in the volume-averaged equations have to be retained. In previous studies, this aspect has never been considered. For each kind of instability, the critical Reynolds number (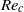${\mathit{Re}}_{c} $) is reported for a wide range of bed slopes (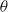$\theta $) and permeabilities (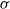$\sigma $). The results show that the free-surface mode follows the behaviour that was theoretically predicted by Benjamin and Yih for impermeable walls and is independent of wall permeability. In contrast, the shear mode shows a high dependence on 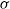$\sigma $: at 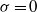$\sigma = 0$ the behaviour of 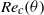${\mathit{Re}}_{c} (\theta )$ recovers the well-known non-monotonic behaviour of the impermeable-wall case, with a minimum at 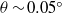$\theta \sim 0. 05\textdegree $. However, with an increase in wall permeability, 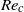${\mathit{Re}}_{c} $ gradually decreases and eventually recovers a monotonic decreasing behaviour. At high values of 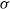$\sigma $, the porous mode of instability also occurs. A physical interpretation of the results is presented on the basis of the interplay between the free-surface-induced perturbation of pressure, the increment of straining due to shear with the increase in slope, and the shear stress condition at the free surface. Finally, the paper investigates the extent to which Squire’s theorem is applicable to the problem presented herein.