Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T16:59:05.659Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction of two axisymmetric bodies falling in tandem at moderate Reynolds numbers

Published online by Cambridge University Press:  19 September 2014

Nicolas Brosse  and
Patricia Ern
Nicolas Brosse
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT; F-31400 Toulouse, France
Patricia Ern*
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT; F-31400 Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study considers the interaction of two identical solid axisymmetric bodies (of diameter 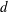$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}d$ and thickness 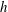$h$) freely falling in a fluid at rest. We determine the domains of existence of the different interaction behaviour of the two bodies (i.e. attraction, repulsion and indifference) as a function of their initial relative position. We then investigate in detail the case of bodies falling in tandem, for both rectilinear and periodic paths, and the associated attraction behaviour. For all the Reynolds numbers and aspect ratios of the bodies (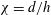$\chi = d/h$) investigated, the trailing body catches up with the leading body. We provide a quantitative description of the kinematics leading to the regrouping of the bodies and analyse its relationship with the wake of the leading body. In the case of rectilinear paths, a dynamical model that takes into account the axial evolution of the wake of the leading body is proposed to reproduce the acceleration observed for the trailing body until a vertical separation distance between the bodies of 1.5 diameters. In parallel, direct numerical simulations (DNS) of the flow about two fixed bodies in tandem in an oncoming flow are carried out, providing a good estimation of the motion of the bodies for separation distances larger than 5 diameters. For periodic paths, the kinematics leading to the regrouping of the bodies is slower than for rectilinear paths. However, in this case, the interaction also leads to significant changes in the characteristics of the oscillatory motion and is strongly dependent on the aspect ratio of the bodies. To explain the observed differences, we consider the effect of the transverse inhomogeneity of the wake of the leading body on the oscillatory motion of the trailing disk.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 208 - 230
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auguste, F.2010 Instabilités de sillage générées derrière un corps solide cylindrique, fixe ou mobile dans un fluide visqueux. PhD thesis, Université Paul Sabatier, Toulouse, France.Google Scholar
Auguste, F., Magnaudet, J. & Fabre, D. 2013 Falling styles of disks. J. Fluid Mech. 719, 388–405.CrossRefGoogle Scholar
Brosse, N. & Ern, P. 2011 Paths of stable configurations resulting from the interaction of two disks falling in tandem. J. Fluids Struct. 27 (5–6), 817–823.CrossRefGoogle Scholar
Carmo, B. S. & Meneghini, J. R. 2006 Numerical investigation of the flow around two circular cylinders in tandem. J. Fluids Struct. 22 (6–7), 979–988.CrossRefGoogle Scholar
Ern, P. & Brosse, N. 2014 Interaction of two axisymmetric bodies falling side by side at moderate Reynolds numbers. J. Fluid Mech. 741, R6.CrossRefGoogle Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of freely rising or falling bodies. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Fernandes, P. C., Ern, P., Risso, F. & Magnaudet, J. 2005 On the zigzag dynamics of freely moving axisymmetric bodies. Phys. Fluids 17 (9), 098107.CrossRefGoogle Scholar
Fernandes, P. C., Ern, P., Risso, F. & Magnaudet, J. 2008 Dynamics of axisymmetric bodies rising along a zigzag path. J. Fluid Mech. 606, 209–223.CrossRefGoogle Scholar
Fernandes, P. C., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely rising axisymmetric bodies. J. Fluid Mech. 573, 479–502.CrossRefGoogle Scholar
Fortes, A. F., Joseph, D. D. & Lundgren, T. S. 1987 Nonlinear mechanics of fluidization of beds of spherical particles. J. Fluid Mech. 177, 467–483.CrossRefGoogle Scholar
Hallez, Y. & Legendre, D. 2011 Interaction between two spherical bubbles rising in a viscous liquid. J. Fluid Mech. 673, 406–431.CrossRefGoogle Scholar
Hu, H. H., Joseph, D. D. & Crochet, M. J. 1992 Direct simulation of fluid particle motions. Theor. Comput. Fluid Dyn. 3, 285–306.CrossRefGoogle Scholar
Jayaweera, K. O. L. F. & Mason, B. J. 1965 The behaviour of freely falling cylinders and cones in a viscous fluid. J. Fluid Mech. 33, 709–720.CrossRefGoogle Scholar
Jayaweera, K. O. L. F., Mason, B. J. & Slack, G. W. 1964 The behaviour of clusters of spheres falling in a viscous fluid. Part 1. Experiment. J. Fluid Mech. 20 (1), 121–128.CrossRefGoogle Scholar
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
Kok, J. B. W. 1993a Dynamics of pair of gas bubbles moving through liquid. Part 1: theory. Eur. J. Mech. B/Fluids 12, 515–540.Google Scholar
Kok, J. B. W. 1993b Dynamics of pair of gas bubbles moving through liquid. Part 2: experiment. Eur. J. Mech. B/Fluids 12, 541–560.Google Scholar
Legendre, D. & Magnaudet, J. 1998 The lift force on a spherical bubble in a viscous linear shear flow. J. Fluid Mech. 368, 81–126.CrossRefGoogle Scholar
Magnaudet, J.1997 The forces acting on bubbles and rigid particles. In ASME Fluids Engng Division Summer Meeting (FEDSM’97), pp. 1–9.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.CrossRefGoogle Scholar
Meneghini, J. R., Saltara, F., Siqueira, C. L. R. & Ferrari, J. A. 2001 Numerical simulation of flow interferance between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 15 (2), 327–350.CrossRefGoogle Scholar
Mittal, S., Kumar, V. & Raghuvanshi, A. 1997 Unsteady incompressible flows past two cylinders in tandem and staggered arrangements. Intl J. Numer. Meth. Fluids 25 (11), 1315–1344.Google Scholar
Mizushima, J. & Norihisa, S. 2005 Instability and transition of flow past two tandem circular cylinders. Phys. Fluids 17 (10), 104107.CrossRefGoogle Scholar
Moore, D. W. 1963 The boundary layer on a spherical gas bubble. J. Fluid Mech. 16 (2), 161–176.CrossRefGoogle Scholar
Natarajan, R. & Acrivos, A. 1993 The instability of the steady flow past spheres and disks. J. Fluid Mech. 254, 323–344.CrossRefGoogle Scholar
Tsuji, Y., Morikawa, Y. & Terashima, Y. 1982 Fluid-dynamic interaction between two spheres. Intl J. Multiphase Flow 8 (1), 71–82.CrossRefGoogle Scholar
Tsuji, T., Narutomi, R., Yokomine, T., Ebara, S. & Shimizu, A. 2003 Unsteady three-dimensional simulation of interactions between flow and two particles. Intl J. Multiphase Flow 29 (9), 1431–1450.CrossRefGoogle Scholar
Yuan, H. & Prosperetti, A. 1994 On the in-line motion of two spherical bubbles in a viscous fluid. J. Fluid Mech. 278, 325–349.CrossRefGoogle Scholar
Zhu, C., Liang, S. C. & Fan, L. S. 1994 Particle wake effects on the drag force of an interactive particle. Intl J. Multiphase Flow 20 (1), 117–129.CrossRefGoogle Scholar

Brosse and Ern supplementary movie

The movie illustrates the interaction of two thick disks (diameter/thickness = 3) falling in tandem at a Reynolds number close to 100. Two fluorescent dyes were used to visualize the wake of the bodies. The camera is moving vertically at the velocity of the leading body (which is falling at 19 mm/s). We observe that the trailing body accelerates thanks to the entrainment provided by the wake of the leading body and catches up with the leading body. Then, the disks separate laterally and eventually fall side by side.

Download Brosse and Ern supplementary movie(Video)
Video 4.5 MB

Brosse and Ern supplementary movie

The movie illustrates the interaction of two thin disks (diameter/thickness = 10) falling in tandem at a Reynolds number close to 80. Two fluorescent dyes were used to visualize the wake of the bodies. The camera is moving vertically at the velocity of the leading body (which is falling at 11 mm/s). We observe that the trailing body accelerates thanks to the entrainment provided by the wake of the leading body and catches up with the leading body. The wakes of the disks merge in a single wake and the bodies continue their fall together adopting a stable Y-configuration.

Download Brosse and Ern supplementary movie(Video)
Video 5.1 MB