Article contents
Interaction of instability waves and a three-dimensional roughness element in a boundary layer
Published online by Cambridge University Press: 06 July 2017
Abstract
The influence of a single roughness element on the evolution of two-dimensional (2-D) Tollmien–Schlichting (TS) waves is investigated experimentally. Experiments are carried out in a region of zero pressure gradient of an airfoil section. Downstream from the disturbance source, TS waves interact with a cylindrical roughness element with a slowly oscillating height. The oscillation frequency of the roughness was approximately 1500 times lower than the wave frequency and approximately 250 times slower than the characteristic time of flow passing the region of transition development. Therefore, the roughness behaved as a quasi-steady disturbance. The set-up enabled us to perform hot-wire measurements phase locked to the waves and to the roughness movement. Experimental results show a scattering of the 2-D waves into oblique ones and a relatively weak distortion of the mean flow for roughness heights as large as 0.2 times the boundary layer displacement thickness (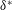 $\unicode[STIX]{x1D6FF}^{\ast }$). Transfer functions for TS wave scattering at the roughness are obtained. Results show an unexpected coincidence in shape with acoustic receptivity functions found in Würz et al. (J. Fluid Mech., vol. 478, 2003, pp. 135–163) for the problem of excitation of TS waves by scattering of acoustic waves at surface roughness. In the present work, the ratio between the incoming 2-D wave amplitude to the amplitude of the scattered oblique waves scaled linearly with the roughness height only for very shallow roughness. For roughness elements higher than
$\unicode[STIX]{x1D6FF}^{\ast }$). Transfer functions for TS wave scattering at the roughness are obtained. Results show an unexpected coincidence in shape with acoustic receptivity functions found in Würz et al. (J. Fluid Mech., vol. 478, 2003, pp. 135–163) for the problem of excitation of TS waves by scattering of acoustic waves at surface roughness. In the present work, the ratio between the incoming 2-D wave amplitude to the amplitude of the scattered oblique waves scaled linearly with the roughness height only for very shallow roughness. For roughness elements higher than 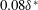 $0.08\unicode[STIX]{x1D6FF}^{\ast }$ and below
$0.08\unicode[STIX]{x1D6FF}^{\ast }$ and below 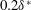 $0.2\unicode[STIX]{x1D6FF}^{\ast }$, the wave scattering exhibited a quadratic variation with respect to the roughness height. In addition, this feature did not vary significantly with respect to TS wave frequency. An analysis of the weakly nonlinear interactions triggered by the roughness element is also carried out, assisted by numerical solution of nonlinear parabolized stability equations, performed for a two-dimensional Blasius boundary layer. A comparison between experiments and simulations reveals that the weakly nonlinear interactions observed are not substantially affected by mean flow distortions that could be produced in the wake of the small and medium sized roughness elements (
$0.2\unicode[STIX]{x1D6FF}^{\ast }$, the wave scattering exhibited a quadratic variation with respect to the roughness height. In addition, this feature did not vary significantly with respect to TS wave frequency. An analysis of the weakly nonlinear interactions triggered by the roughness element is also carried out, assisted by numerical solution of nonlinear parabolized stability equations, performed for a two-dimensional Blasius boundary layer. A comparison between experiments and simulations reveals that the weakly nonlinear interactions observed are not substantially affected by mean flow distortions that could be produced in the wake of the small and medium sized roughness elements (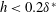 $h<0.2\unicode[STIX]{x1D6FF}^{\ast }$). From a practical perspective, results suggest that scattering coefficients might be employed to include the effect of isolated and medium sized roughness elements in transition prediction tools developed for smooth surfaces.
$h<0.2\unicode[STIX]{x1D6FF}^{\ast }$). From a practical perspective, results suggest that scattering coefficients might be employed to include the effect of isolated and medium sized roughness elements in transition prediction tools developed for smooth surfaces.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 9
- Cited by



