Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-06T07:12:50.381Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction of a vortex ring with a single bubble: bubble and vorticity dynamics

Published online by Cambridge University Press:  29 May 2015

Narsing K. Jha  and
R. N. Govardhan
Narsing K. Jha
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560012, India
R. N. Govardhan*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The interaction of a single bubble with a single vortex ring in water has been studied experimentally. Measurements of both the bubble dynamics and vorticity dynamics have been done to help understand the two-way coupled problem. The circulation strength of the vortex ring (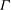${\it\Gamma}$) has been systematically varied, while keeping the bubble diameter (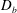$D_{b}$) constant, with the bubble volume to vortex core volume ratio (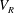$V_{R}$) also kept fixed at about 0.1. The other important parameter in the problem is a Weber number based on the vortex ring strength 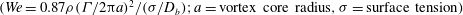$(\mathit{We}=0.87{\it\rho}({\it\Gamma}/2{\rm\pi}a)^{2}/({\it\sigma}/D_{b});a=\text{vortex core radius},{\it\sigma}=\text{surface tension})$, which is varied over a large range, 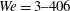$\mathit{We}=3{-}406$. The interaction between the bubble and ring for each of the 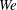$\mathit{We}$ cases broadly falls into four stages. Stage I is before capture of the bubble by the ring where the bubble is drawn into the low-pressure vortex core, while in stage II the bubble is stretched in the azimuthal direction within the ring and gradually broken up into a number of smaller bubbles. Following this, in stage III the bubble break-up is complete and the resulting smaller bubbles slowly move around the core, and finally in stage IV the bubbles escape. Apart from the effect of the ring on the bubble, the bubble is also shown to significantly affect the vortex ring, especially at low 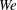$\mathit{We}$ (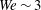$\mathit{We}\sim 3$). In these low-$\mathit{We}$ cases, the convection speed drops significantly compared to the base case without a bubble, while the core appears to fragment with a resultant large decrease in enstrophy by about 50 %. In the higher-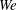$\mathit{We}$ cases (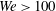$\mathit{We}>100$), there are some differences in convection speed and enstrophy, but the effects are relatively small. The most dramatic effects of the bubble on the ring are found for thicker core rings at low 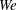$\mathit{We}$ (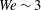$\mathit{We}\sim 3$) with the vortex ring almost stopping after interacting with the bubble, and the core fragmenting into two parts. The present idealized experiments exhibit many phenomena also seen in bubbly turbulent flows such as reduction in enstrophy, suppression of structures, enhancement of energy at small scales and reduction in energy at large scales. These similarities suggest that results from the present experiments can be helpful in better understanding interactions of bubbles with eddies in turbulent flows.

JFM classification

Flow Control: Drag reduction Multiphase and Particle-laden Flows: Gas/liquid flow Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 773 , 25 June 2015 , pp. 460 - 497
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Arndt, R. E. A., Arakeri, V. H. & Higuchi, H. 1991 Some observations of tip-vortex cavitation. J. Fluid Mech. 229, 269–289.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
van den Berg, T. H., Luther, S. & Lohse, D. 2006 Energy spectra in microbubbly turbulence. Phys. Fluids 18, 038103.Google Scholar
Brücker, C. 1999 Structure and dynamics of the wake of bubbles and its relevance for bubble interaction. Phys. Fluids 11, 1781–1796.Google Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 14–188.CrossRefGoogle Scholar
Ceccio, S. L. 2010 Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 42, 183–203.Google Scholar
Chahine, G. L. 1995 Bubble interactions with vortices. In Fluid Vortices (ed. Green, S.), Fluid Mechanics and Its Applications, vol. 30, pp. 783–828. Springer Science & Business Media.Google Scholar
Choi, J. & Ceccio, S. L. 2007 Dynamics and noise emission of vortex cavitation bubbles. J. Fluid Mech. 575, 1–26.Google Scholar
Choi, J., Hsiao, C. T., Chahine, G. L. & Ceccio, S. L. 2009 Growth, oscillation and collapse of vortex cavitation bubbles. J. Fluid Mech. 624, 255–279.Google Scholar
Cihonski, A. J., Finn, J. R. & Apte, S. V. 2013 Volume displacement effects during bubble entrainment in a travelling vortex ring. J. Fluid Mech. 721, 225–267.Google Scholar
Dabiri, J. O., Bose, S., Gemmell, B. J., Colin, S. P. & Costello, J. H. 2013 An algorithm to estimate unsteady and quasi-steady pressure fields from velocity field measurements. J. Expl Biol. 217, 092767.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.Google Scholar
Dixit, H. N. & Govindarajan, R. 2011 Stability of a vortex in radial density stratification: role of wave interactions. J. Fluid Mech. 679, 582–615.Google Scholar
Dritschel, D. G. 1986 The nonlinear evolution of rotating configurations of uniform vorticity. J. Fluid Mech. 172, 157–182.Google Scholar
Ferrante, A. & Elghobashi, S. 2004 On the physical mechanisms of drag reduction in a spatially developing turbulent boundary layer laden with microbubbles. J. Fluid Mech. 503, 345–355.Google Scholar
Ferrante, A. & Elghobashi, S. 2007 On the effects of microbubbles on Taylor–Green vortex flow. J. Fluid Mech. 572, 145–177.CrossRefGoogle Scholar
Fukumoto, Y. & Moffatt, H. K. 2000 Motion and expansion of a viscous vortex ring. Part 1. A higher-order asymptotic formula for the velocity. J. Fluid Mech. 417, 1–45.Google Scholar
Gan, L., Dawson, J. R. & Nickels, T. B. 2012 On the drag of turbulent vortex rings. J. Fluid Mech. 709, 85–105.Google Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.Google Scholar
Gils, D. P. M. V., Guzman, D. N., Sun, C. & Lohse, D. 2013 The importance of bubble deformability for strong drag reduction in bubbly turbulent Taylor–Couette flow. J. Fluid Mech. 722, 317–347.Google Scholar
Glezer, A. 1988 The formation of vortex rings. Phys. Fluids 31 (12), 3532–3542.Google Scholar
Govindarajan, R. & Sahu, K. C. 2014 Instabilities in viscosity-stratified flow. Annu. Rev. Fluid Mech. 46, 331–353.Google Scholar
Haberman, W. L. & Morton, R. K.1953 An experimental investigation of the drag and shape of air bubbles rising in various liquids. David W. Taylor Model Basin Rep. 802.Google Scholar
Herpin, S., Stanislas, M., Foucaut, J. M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.Google Scholar
Hinze, J. O. 1955 Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1, 289–295.Google Scholar
Jacob, B., Olivieri, A., Miozzi, M., Campana, E. F. & Piva, R. 2010 Drag reduction by microbubbles in a turbulent boundary layer. Phys. Fluids 22, 115104.Google Scholar
Kolmogorov, A. N. 1949 On the breakage of drops in a turbulent flow. Dokl. Akad. Nauk SSSR 66, 825–828.Google Scholar
Leweke, T. & Williamson, C. H. K. 1998 Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85–119.Google Scholar
Lu, J., Fernández, A. & Tryggvason, G. 2005 The effect of bubbles on the wall drag in a turbulent channel flow. Phys. Fluids 17, 095102.CrossRefGoogle Scholar
Madavan, N. K., Deutsch, S. & Merkle, C. L. 1985 Measurements of local skin friction in a microbubble-modified turbulent boundary layer. J. Fluid Mech. 156, 237–256.CrossRefGoogle Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.CrossRefGoogle Scholar
Martínez-Bazán, C., Montañés, J. L. & Lasheras, J. C. 1999 On the breakup of an air bubble injected into a fully developed turbulent flow. Part 2. Size PDF of the resulting daughter bubbles. J. Fluid Mech. 401, 183–207.CrossRefGoogle Scholar
Mazzitelli, I. M., Lohse, D. & Toschi, F. 2003 On the relevance of the lift force in bubbly turbulence. J. Fluid Mech. 488, 283–313.Google Scholar
Mougin, G. & Magnaudet, J. 2001 Path instability of a rising bubble. Phys. Rev. Lett. 88, 01450.Google Scholar
Murai, Y. 2014 Frictional drag reduction by bubble injection. Exp. Fluids 55, 1–28.CrossRefGoogle Scholar
Norbury, J. 1973 A family of steady vortex rings. J. Fluid Mech. 57, 417–431.CrossRefGoogle Scholar
O’Farrell, C. & Dabiri, J. O. 2012 Perturbation response and pinch-off of vortex rings and dipoles. J. Fluid Mech. 704, 280–300.Google Scholar
Oweis, G. F., Van der Hout, I. E., Iyer, C., Tryggvason, G. & Ceccio, S. L. 2005 Capture and inception of bubbles near line vortices. Phys. Fluids 17, 022105.CrossRefGoogle Scholar
Revuelta, A. 2010 On the interaction of a bubble and a vortex ring at high Reynolds numbers. Eur. J. Mech. (B/Fluids) 29, 119–126.Google Scholar
Risso, F. & Fabre, J. 1998 Oscillations and breakup of a bubble immersed in a turbulent field. J. Fluid Mech. 372, 323–355.CrossRefGoogle Scholar
Sanders, W. C., Winkel, E. S., Dowling, D. R., Perlin, M. & Ceccio, S. L. 2006 Bubble friction drag reduction in a high-Reynolds-number flat-plate turbulent boundary layer. J. Fluid Mech. 552, 353–380.Google Scholar
Shinnar, R. 1961 On the behaviour of liquid dispersions in mixing vessels. J. Fluid Mech. 10, 259–275.Google Scholar
Sridhar, G. & Katz, J. 1995 Drag and lift forces on microscopic bubbles entrained by a vortex. Phys. Fluids 7, 389–399.Google Scholar
Sridhar, G. & Katz, J. 1999 Effect of entrained bubbles on the structure of vortex rings. J. Fluid Mech. 397, 171–202.Google Scholar
Thorpe, S. A. 1992 Bubble clouds and the dynamics of the upper ocean. Q. J. R. Meteorol. Soc. 118, 1–22.Google Scholar
Uchiyama, T. & Kusamichi, S. 2013 Interaction of bubbles with vortex ring launched into bubble plume. Adv. Chem. Engng Sci. 3, 207–217.CrossRefGoogle Scholar
Widnall, S. E., Bliss, D. B. & Tsai, C. Y. 1974 The instability of short waves on a vortex ring. J. Fluid Mech. 66, 35–47.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar