Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T11:51:14.148Z Has data issue: false hasContentIssue false
  • English
  • Français

Intensification of non-uniformity in convergent near-conical hypersonic flow

Published online by Cambridge University Press:  22 November 2021

Junze Ji ,
Zhufei Li Open the ORCID record for Zhufei Li [Opens in a new window] ,
Enlai Zhang Open the ORCID record for Enlai Zhang [Opens in a new window] ,
Dongxian Si  and
Jiming Yang
Junze Ji
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
Zhufei Li*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
Enlai Zhang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
Dongxian Si
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
Jiming Yang*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

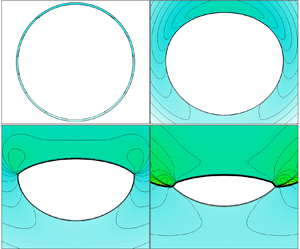
The inevitable formation of a Mach disk at the central axis of a convergent conical shock wave may suffer from fundamental changes when the flow deviates from the axisymmetric condition. In this paper, the behaviours of near-conical shocks, which are generated by a circular ring wedge of $10^{\circ }$ at typical angles of attack (AoAs), are investigated at a free stream Mach number of 6 in a shock tunnel. To reveal the characteristics and mechanism of the flow, numerical analyses are carried out under the same conditions. The results indicate that when the flow deviates from axial symmetry, the circumferential non-uniformity is remarkably intensified as the shock converges downstream. The converging centre shifts against the inclination of the incoming flow and moves to the leeward side. For a sufficiently small AoA, the formation of a Mach disk remains similar to that in the axisymmetric case, although the Mach disk shrinks in size and is slightly flattened. As the circumferential non-uniformity of the shock increases at an AoA of approximately $3^{\circ }$, a pair of kinks separate the shock surface into two discontinuous segments with the stronger shock segment on the windward side and the weaker shock segment on the leeward side. When the AoA increases further, the shrinkage of the Mach disk continuously occurs, and the Mach disk is eventually replaced by a regular reflection. The discontinuity of a convergent shock with flattening on the separated shock segments and the insufficient strength increase during the subsequent convergence are responsible for the appearance of regular reflection.

JFM classification

Compressible Flows: Shock waves Compressible Flows: Hypersonic Flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 931 , 25 January 2022 , A8
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ben-Dor, G. 2007 Shock Wave Reflection Phenomena, 2nd edn. Springer.Google Scholar
Ben-Dor, G. & Takayama, K. 1986 The dynamics of the transition from Mach to regular reflection over concave cylinders. Israel J. Technol. 23 (3), 71–74.Google Scholar
Ferri, A. 1946 Application of the method of characteristics to supersonic rotational flow. NACA Tech. Rep. 841. National Advisory Committee for Aeronautics.Google Scholar
Filippi, A.A. & Skews, B.W. 2017 Supersonic flow fields resulting from axisymmetric internal surface curvature. J. Fluid Mech. 831, 271–288.CrossRefGoogle Scholar
Filippi, A.A. & Skews, B.W. 2018 Streamlines behind curved shock waves in axisymmetric flow fields. Shock Waves 28 (4), 785–793.CrossRefGoogle Scholar
Courant, R. & Friedrichs, K.O. 1948 Supersonic Flow and Shock Waves. Springer.Google Scholar
Gounko, Y.P. 2017 Patterns of steady axisymmetric supersonic compression flows with a Mach disk. Shock Waves 27 (3), 495–506.CrossRefGoogle Scholar
Isakova, N.P., Kraiko, A.N., Pyankov, K.S. & Tillyayeva, N.I. 2012 The amplification of weak shock waves in axisymmetric supersonic flow and their reflection from an axis of symmetry. J. Appl. Math. Mech. 76 (4), 451–465.CrossRefGoogle Scholar
Li, H., Chpoun, A. & Ben-Dor, G. 1999 Analytical and experimental investigations of the reflection of asymmetric shock waves in steady flows. J. Fluid Mech. 390, 25–43.CrossRefGoogle Scholar
Li, Z.-F., Gao, W.-Z., Jiang, H.-L. & Yang, J.-M. 2013 Unsteady behaviors of a hypersonic inlet caused by throttling in shock tunnel. AIAA J. 51 (10), 2485–2492.CrossRefGoogle Scholar
Liou, M.-S. 1996 A sequel to AUSM: AUSM$^+$. J. Comput. Phys. 129 (2), 364–382.CrossRefGoogle Scholar
Mölder, S. 1967 Internal, axisymmetric, conical flow. AIAA J. 5 (7), 1252–1255.CrossRefGoogle Scholar
Mölder, S., Gulamhussein, A., Timofeev, E. & Voinovich, P. 1997 Focusing of conical shocks at the centre-line of symmetry. In Shock Waves (ed. A.F.P. Houwing & A. Paull), pp. 875–880. Panther Publishing and Printing.Google Scholar
Mölder, S. 2016 Curved shock theory. Shock Waves 26 (4), 337–353.CrossRefGoogle Scholar
Mölder, S. 2017 a Reflection of curved shock waves. Shock Waves 27 (5), 699–720.CrossRefGoogle Scholar
Mölder, S. 2017 b Flow behind concave shock waves. Shock Waves 27 (5), 721–730.CrossRefGoogle Scholar
Mölder, S. 2017 c Shock detachment from curved wedges. Shock Waves 27 (5), 731–745.CrossRefGoogle Scholar
Rylov, A.I. 1990 On the impossibility of regular reflection of a steady-state shock wave from the axis of symmetry. J. Appl. Math. Mech. 54 (2), 201–203.CrossRefGoogle Scholar
Shoesmith, B., Mölder, S., Ogawa, H. & Timofeev, E. 2017 Shock reflection in axisymmetric internal flows. In Shock Wave Interactions (ed. K. Kontis), pp. 355–366. Springer.CrossRefGoogle Scholar
Shi, C.-G., Han, W.-Q., Deiterding, R., Zhu, C.-X. & You, Y.-C. 2020 Second-order curved shock theory. J. Fluid Mech. 891, A21.CrossRefGoogle Scholar
Shi, C.-G., Zhu, C.-X., You, Y.-C. & Zhu, G.-S. 2021 Method of curved-shock characteristics with application to inverse design of supersonic flowfields. J. Fluid Mech. 920, A36.CrossRefGoogle Scholar
Tan, L.-H., Ren, Y.-X. & Wu, Z.-N. 2006 Analytical and numerical study of the near flow field and shape of the Mach stem in steady flows. J. Fluid Mech. 546, 341–362.CrossRefGoogle Scholar
You, Y.-C., Zhu, C.-X. & Guo, J.-L. 2009 Dual waverider concept for the integration of hypersonic inward-turning inlet and airframe forebody. AIAA Paper 2009-7421.CrossRefGoogle Scholar
You, Y.-C. 2011 An overview of the advantages and concerns of hypersonic inward turning inlets. AIAA Paper 2011-2269.CrossRefGoogle Scholar
Zhang, E.-L., Li, Z.-F., Ji, J.-Z., Si, D.-X. & Yang, J.-M. 2021 Converging near-elliptic shock waves. J. Fluid Mech. 909, A2.CrossRefGoogle Scholar
Zuo, F.-Y. & Mölder, S. 2019 Hypersonic wavecatcher intakes and variable-geometry turbine based combined cycle engines. Prog. Aerosp. Sci. 106, 108–114.CrossRefGoogle Scholar
Zuo, F.-Y., Mölder, S. & Chen, G. 2020 Performance of wavecatcher intakes at angles of attack and sideslip. Chin. J. Aeronaut. 34 (7), 244–256.CrossRefGoogle Scholar