Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T05:12:16.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability of pressure-driven gas–liquid two-layer channel flows in two and three dimensions

Published online by Cambridge University Press:  15 June 2018

Lennon Ó Náraigh Open the ORCID record for Lennon Ó Náraigh [Opens in a new window]  and
Peter D. M. Spelt
Lennon Ó Náraigh*
Affiliation:
School of Mathematics and Statistics, University College Dublin, Belfield, Dublin 4, Ireland Laboratoire de Mécanique des Fluides et d’Acoustique (LMFA), UMR CNRS 5509, Université de Lyon, 69134 Écully, France
Peter D. M. Spelt
Affiliation:
School of Mathematics and Statistics, University College Dublin, Belfield, Dublin 4, Ireland Laboratoire de Mécanique des Fluides et d’Acoustique (LMFA), UMR CNRS 5509, Université de Lyon, 69134 Écully, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study unstable waves in gas–liquid two-layer channel flows driven by a pressure gradient, under stable stratification, not assumed to be set in motion impulsively. The basis of the study is direct numerical simulation (DNS) of the two-phase Navier–Stokes equations in two and three dimensions for moderately large Reynolds numbers, accompanied by a theoretical description of the dynamics in the linear regime (Orr–Sommerfeld–Squire equations). The results are compared and contrasted across a range of density ratios 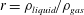$r=\unicode[STIX]{x1D70C}_{liquid}/\unicode[STIX]{x1D70C}_{gas}$. Linear theory indicates that the growth rate of small-amplitude interfacial disturbances generally decreases with increasing $r$; at the same time, the cutoff wavenumbers in both streamwise and spanwise directions increase, leading to an ever-increasing range of unstable wavenumbers, albeit with diminished growth rates. The analysis also demonstrates that the most dangerous mode is two-dimensional in all cases considered. The results of a comparison between the DNS and linear theory demonstrate a consistency between the two approaches: as such, the route to a three-dimensional flow pattern is direct in these cases, i.e. through the strong influence of the linear instability. We also characterize the nonlinear behaviour of the system, and we establish that the disturbance vorticity field in two-dimensional systems is consistent with a mechanism proposed previously by Hinch (J. Fluid Mech., vol. 144, 1984, p. 463) for weakly inertial flows. A flow-pattern map constructed from two-dimensional numerical simulations is used to describe the various flow regimes observed as a function of density ratio, Reynolds number and Weber number. Corresponding simulations in three dimensions confirm that the flow-pattern map can be used to infer the fate of the interface there also, and show strong three-dimensionality in cases that exhibit violent behaviour in two dimensions, or otherwise the development of behaviour that is nearly two-dimensional behaviour possibly with the formation of a capillary ridge. The three-dimensional vorticity field is also analysed, thereby demonstrating how streamwise vorticity arises from the growth of otherwise two-dimensional modes.

JFM classification

Instability: Instability Waves/Free-surface Flows: Waves/Free-surface Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 1 - 34
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1967 Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Benjamin, T. B. 1959 Shearing flow over a wavy boundary. J. Fluid Mech. 6, 161–205.Google Scholar
Blennerhassett, P. J. 1980 On the generation of waves by wind. Phil. Trans. R. Soc. Lond. A 298 (1441), 451–494.Google Scholar
Boeck, T., Li, J., López-Pagés, E., Yecko, P. & Zaleski, S. 2007 Ligament formation in sheared liquid–gas layers. Theor. Comput. Fluid Dyn. 21, 59–76.Google Scholar
Boomkamp, P. A. M., Boersma, B. J., Miesen, R. H. M. & Beijnon, G. V. 1997 A Chebyshev collocation method for solving two-phase flow stability problems. J. Comput. Phys. 132, 191–200.Google Scholar
Boomkamp, P. A. M. & Miesen, R. H. M. 1996 Classification of instabilities in parallel two-phase flow. Intl J. Multiphase Flow 22, 67–88.Google Scholar
Buffat, M., Le Penven, L., Cadiou, A. & Montagnier, J. 2014 DNS of bypass transition in entrance channel flow induced by boundary layer interaction. Eur. J. Mech. (B/Fluids) 43, 1–13.Google Scholar
Charogiannis, A., Denner, F., van Wachem, B. G. M., Kalliadasis, S. & Markides, C. N. 2017 Detailed hydrodynamic characterization of harmonically excited falling-film flows: a combined experimental and computational study. Phys. Rev. Fluids 2, 014002.Google Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Math. Comput. 22, 745–762.Google Scholar
Craik, A. D. D. 1985 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Fannon, J., Loiseau, J.-C., Valluri, P., Bethune, I. & Ó Náraigh, L. 2016 Simplified TPLS as a learning tool for high-performance computational fluid dynamics. Eur. J. Phys. 37, 045001.Google Scholar
Fuster, D., Matas, J.-P., Marty, S., Popinet, S., Hoepffner, J., Cartellier, A. & Zaleski, S. 2013 Instability regimes in the primary breakup region of planar coflowing sheets. J. Fluid Mech. 736, 150–176.Google Scholar
Hewitt, G. F. 1982 Flow regimes. In Handbook of Multiphase Systems (ed. Hetsroni, G.). McGraw-Hill.Google Scholar
Hinch, E. J. 1984 A note on the mechanisms of the instability at the interface between two shearing fluids. J. Fluid Mech. 144, 463–465.Google Scholar
Hooper, A. P. & Boyd, W. G. C. 1983 Shear-flow instability at the interface between two viscous fluids. J. Fluid Mech. 128, 507–528.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instability in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
Jiang, G.-S. & Shu, C.-W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228.Google Scholar
Kelly, R. E., Goussis, D. A., Lin, S. P. & Hsu, F. K. 1989 The mechanism for surface wave instability in film flow down an inclined plane. Phys. Fluids A 1, 819–828.Google Scholar
Ling, Y., Fuster, D., Zaleski, S. & Tryggvason, G. 2017 Spray formation in a quasiplanar gas–liquid mixing layer at moderate density ratios: a numerical closeup. Phys. Rev. Fluids 2, 014005.Google Scholar
Matas, J.-P. 2015 Inviscid versus viscous instability mechanism of an air–water mixing layer. J. Fluid Mech. 768, 375–387.Google Scholar
Ó Náraigh, L., Spelt, P. D. M., Matar, O. K. & Zaki, T. A. 2011 Interfacial instability of turbulent two-phase stratified flow: pressure-driven flow and thin liquid films. Intl J. Multiphase Flow 37, 812–830.Google Scholar
Ó Náraigh, L., Spelt, P. D. M. & Shaw, S. J. 2013a Absolute linear instability in laminar and turbulent gas–liquid two-layer channel flow. J. Fluid Mech. 714, 58–94.Google Scholar
Ó Náraigh, L., Valluri, P., Scott, D. M., Bethune, I. & Spelt, P. D. M.2013b TPLS: high resolution direct numerical simulation (DNS) of two-phase flows. Available at: http://sourceforge.net/projects/tpls/.Google Scholar
Ó Náraigh, L., Valluri, P., Scott, D. M., Bethune, I. & Spelt, P. D. M. 2014 Linear instability, nonlinear instability and ligament dynamics in three-dimensional laminar two-layer liquid–liquid flows. J. Fluid Mech. 750, 464–506.Google Scholar
Otto, T., Rossi, M. & Boeck, T. 2013 Viscous instability of a sheared liquid–gas interface: dependence on fluid properties and basic velocity profile. Phys. Fluids 25 (3), 032103.Google Scholar
Russo, G. & Smereka, P. 2000 A remark on computing distance functions. J. Comput. Phys. 163, 51–67.Google Scholar
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. E 15, 357–369.Google Scholar
Sahu, K. C. & Matar, O. K. 2011 Three-dimensional convective and absolute instabilities in pressure-driven two-layer channel flow. Intl J. Multiphase Flow 37 (8), 987–993.Google Scholar
Scardovelli, R. & Zaleski, S. 1999 Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 31, 567–603.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Solomenko, Z., Spelt, P. D. M., Ó Náraigh, L. & Alix, P. 2017 Mass conservation and reduction of parasitic interfacial waves in level-set methods for the numerical simulation of two-phase flows: a comparative study. Intl J. Multiphase Flow 95, 235–256.Google Scholar
Sussman, M. & Fatemi, E. 1999 An efficient, interface-preserving level set redistancing algorithm and its application to interfacial incompressible fluid flow. SIAM J. Sci. Comput. 20, 1165–1191.Google Scholar
Valluri, P., Ó Náraigh, L., Ding, H. & Spelt, P. D. M. 2010 Linear and nonlinear spatio-temporal instability in laminar two-layer flows. J. Fluid Mech. 656, 458–480.Google Scholar
Yiantsios, S. G. & Higgins, B. G. 1988 Linear stability of plane Poiseuille flow of two superposed fluids. Phys. Fluids 31, 3225–3238. Corrigendum: Phys. Fluids A 1 897 (1989).Google Scholar
Yih, C. S. 1967 Instability due to viscosity stratification. J. Fluid Mech. 27, 337–352.Google Scholar