Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T10:24:48.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability of a vortex sheet leaving a right-angled wedge

Published online by Cambridge University Press:  15 August 2016

Anthony M. J. Davis  and
Stefan G. Llewellyn Smith
Anthony M. J. Davis
Affiliation:
Department of Mechanical and Aerospace Engineering, Jacobs School of Engineering, UCSD, 9500 Gilman Drive, La Jolla, CA 92093-0411, USA
Stefan G. Llewellyn Smith*
Affiliation:
Department of Mechanical and Aerospace Engineering, Jacobs School of Engineering, UCSD, 9500 Gilman Drive, La Jolla, CA 92093-0411, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the dynamics of a semi-infinite vortex sheet attached not to a semi-infinite plate but instead to a rigid right-angled wedge, with the sheet aligned along one of its edges. Our approach to this problem, which was suggested by David Crighton, accords well with the fundamental ethos of Crighton’s work, which was characterized by ‘the application of rigorous mathematical approximations to fluid mechanical idealizations of practically relevant problems’ (Ffowcs Williams, Annu. Rev. Fluid Mech., vol. 34, 2002, pp. 37–49). The resulting linearised unsteady potential flow is forced by an oscillatory dipole in the uniform stream passing along the top of the wedge, while there is stagnant fluid in the remaining quadrant. Spatial instability is considered according to well-established methods: causality is enforced by allowing the frequency to become temporarily complex. The essentially quadrant-type geometry replaces the usual Wiener–Hopf technique by the Mellin transform. The core difficulty is that a first-order difference equation of period 4 requires a solution of period unity. As a result, the complex fourth roots 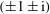$(\pm 1\pm \text{i})$ of 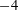$-4$ appear in the complementary function. The Helmholtz instability wave is excited and requires careful handling to obtain explicit results for the amplitude of the instability wave.

JFM classification

Instability: Instability Wakes/Jets: Shear layers Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 803 , 25 September 2016 , pp. 1 - 17
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnes, E. W. 1899 The genesis of the double Gamma functions. Proc. Lond. Math. Soc. 31, 358–381.Google Scholar
Bechert, D. & Pfizenmaier, E. 1975 Optical compensation measurements on the unsteady exit condition at a nozzle discharge edge. J. Fluid Mech. 71, 123–144.CrossRefGoogle Scholar
Crighton, D. G. 1972 Radiation properties of the semi-infinite vortex sheet. Proc. R. Soc. Lond. A 330, 185–198.Google Scholar
Crighton, D. G. 1985 The Kutta condition in unsteady flow. Annu. Rev. Fluid Mech. 17, 411–445.CrossRefGoogle Scholar
Crighton, D. G. & Leppington, F. G. 1974 Radiation properties of the semi-infinite vortex sheet: the initial-value problem. J. Fluid Mech. 64, 393–414.Google Scholar
Daniels, P. G. 1978 On the unsteady Kutta condition. Q. J. Mech. Appl. Maths 31, 49–75.Google Scholar
Jones, D. S. & Morgan, J. D. 1972 The instability of a vortex sheet on a subsonic stream under acoustic radiation. Proc. Camb. Phil. Soc. 72, 465–488.Google Scholar
Lawrie, J. B. 1990 Surface-tension-driven flow in a wedge. Q. J. Mech. Appl. Maths 43, 251–273.CrossRefGoogle Scholar
Lawrie, J. B. & King, A. C. 1994 Exact solution to a class of functional difference equations with application to a moving contact line flow. Eur. J. Appl. Maths 5, 141–157.CrossRefGoogle Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. & Clark, C. W.(Eds) 2010 NIST Handbook of Mathematical Functions. Cambridge University Press.Google Scholar
Orszag, S. A. & Crow, S. C. 1970 Instability of a vortex sheet leaving a semi-infinite plate. Stud. Appl. Maths 49, 167–181.Google Scholar
Peake, N. 1994 The viscous interaction between sound waves and the trailing edge of a supersonic splitter plate. J. Fluid Mech. 264, 321–342.CrossRefGoogle Scholar
Rabchuk, J. A. 2000 Receptivity to harmonic forcing of a finite-width mixing layer just downstream of the trailing edge of a flat plate. Phys. Fluids 12, 1749–1761.Google Scholar
Samanta, A. & Freund, J. B. 2008 Finite wavelength scattering of incident vorticity and acoustic waves at a shrouded-jet exit. J. Fluid Mech. 612, 407–438.Google Scholar
Williams, W. E. 1959 Diffraction of an E-polarised plane wave by an imperfectly conducting wedge. Proc. R. Soc. Lond. A 252, 376–393.Google Scholar